斯坦福CS229机器学习课程笔记三：感知机、Softmax回归

为了给课程的前四讲画上一个句号，这里补充两个前四讲中NG大神提到过的模型。

The perceptron learning algorithm 感知机

模型：

 从模型上来看感知机与逻辑回归十分相似，只不过逻辑回归的g函数是逻辑函数（又称sigmoid函数），它是一条从y值0到1的连续曲线。当z→∞，g(z)→1；当z → −∞，g(z)→0。 g(z) = 1/(1+e^-z)

 而感知机的g函数是分段函数，只输出0和1。 虽然和逻辑回归形式上相近，但是很难为感知机的预测加上概率解释，也很难说感知机算法是源于最大化似然函数，

不过Andrew Ng还是给出了训练感知机模型的梯度上升算法（和逻辑回归一样）： 

Softmax回归

1.模型

通过之前的学习，我们知道逻辑回归基于伯努利二项分布可以输出二元变量发生的概率（比如：用户是否点击广告链接的概率，用户是否回访的概率），以此解决二元分类问题。但是当我们想进行多元分类时（比如：想根据用户在未来一个月内的充值金额，划分为低充值用户、中等充值用户、充值大户），这时逻辑回归就不够用了。这时我们可以使用能够输出多元变量相应概率的多元分布 multinomial distribution，依然从广义线性模型的角度来构造模型： 1.1 多元分布属于指数分布族（输出变量有k个不同取值，相应的多元分布就有k-1个参数，Φ_k表示第k个值发生的概率，最后一个参数可以用1减去前k-1个参数的和得到，因此只需要k-1个参数） 对于之前讲到过的正态分布和伯努利分布都有T(y)=y，但这里需要定义一下T(y)：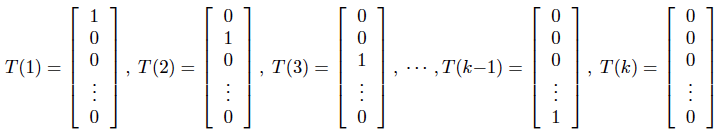

 另外，令： (T(y))_i 表示向量T(y)的第i个元素，比如：(T(1))₁=1 (T(1))₂=0 1{.}是一个指示函数，1{True} = 1, 1{False} = 0 (T(y))_i = 1{y = i} 由此可以推出多元分布的指数分布族形式：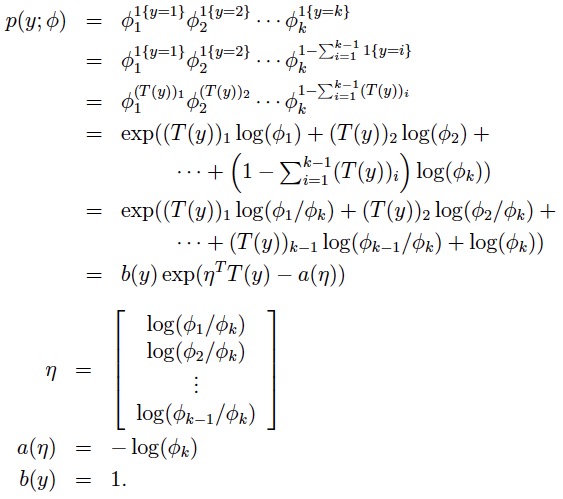

 1.2 目标是预测T(y)的期望，由于T(y)是一个向量，所以得到的输出也会是一个期望的向量，其中每个元素为：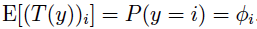

 正好对应了多元变量中，每个取值发生的概率。 1.3 由多项分布的指数分布族表现形式中η关于Φ的函数，可以反推出

 这就是softmax函数，也是softmax回归的名称来由，最后将η=θT x带入公式，最终我们得到softmax回归的模型： 

2.策略

对于概率模型，仍然是使用最大化对数似然函数的方法：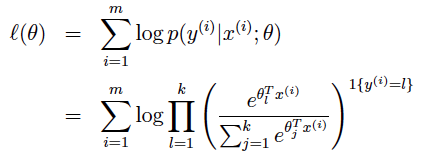 

3.算法

可通过梯度上升算法求得最优解，值得注意的是softmax回归将会得到一个参数的k-1*n矩阵。（注：类别k对应的参数θk=0）