洛谷 P4936 Agent1

题目背景

2018年11月17日，中国香港将会迎来一场XM大战，是世界各地的ENLIGHTENED与RESISTANCE开战的地点，某地 的ENLIGHTENED总部也想派Agent去参加这次的XM大战，与世界其他地方的ENLIGHTENED并肩作战。

题目描述

某地的ENLIGHTENED总部总部有NN个Agent，每个Agent的能力值互不相同，现在ENLIGHTENED行动指挥想要派出A,BA,B两队Agent去参加XM大战。但是参加大战的两个队伍要满足两个要求：

1. AA队中能力最大的Agent的能力值要小于BB队能力最弱的Agent的能力值。
2. A,BA,B两队都要有人参战。

并不一定所有的Agent都要去参加XM大战的，心急的ENLIGHTENED行动指挥想知道有多少种安排Agent参加大战的方案。由于答案可能很大，所以只需要你求出答案模(10^9+7)(109+7)的值就可以了。

输入格式

输入仅一行，为一个整数NN。

输出格式

输出答案模(10^9+7)(109+7)的值。

输入输出样例

输入 #1复制

3

输出 #1复制

5

输入 #2复制

6

输出 #2复制

129

说明/提示

对于20\%20%的数据 N leq 10N≤10

对于40\%40%的数据 N leq 10^3N≤103

对于60\%60%的数据 N leq 10^5N≤105

对于100\%100%的数据 N leq 10^9N≤109

思路：据我观察这是一个高考数学原题的加强版（雾）。

具体是怎么做呢。。。首先我们注意到元素大小各不相同，那我们不妨采用离散化的思想，将这n个元素直接赋值为1~n，然后对于A，B这两个集合的选择方案，我们这里有一个非常巧妙的做法，那就是先从序列中选择一些元素，将其都放入一个集合中并对其进行从小到大定序，显然，当我们选择了k个元素时，这k个元素中间的“空隙”有k-1个，我们不妨再采用隔板法的思想，在空隙中放置1块隔板，显然，这块隔板将原集合一分为二，又令左边的部分为A，右边的部分为B，这样一定满足A中最大的小于B中最小的。这样对于每一个k，划分的方案数为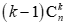,而总方案数就是对于每一个k<=n求和，也就是,我们观察数据发现，如果单独枚举k从1~n，不论是组合数逆元还是卢卡斯定理对于40%的数据都是妥妥的过不去，那么接下来，我们就要动用我们的数学知识去整理这个式子，消去组合数（

首先：注意到

对于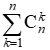，利用二项式定理的基本结论，不难发现就是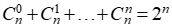缺了个Cn0也就是缺1，故等于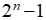

对于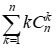直接求不是很好求，但是如果我们认真听数学老师讲课的话（雾），我们就会发现这道题竟然可以用求导来解（

不妨设，对等式三边同时求导，得

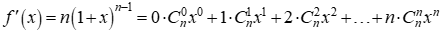
用赋值法，得：

综合各式，最终答案就是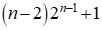,用快速幂求即可。

代码：

#include<iostream> 
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
ll mod = 1e9 + 7;
ll ksm(ll x, ll y)
{
    ll ret = 1, base = x;
    while(y)
    {
        if(y & 1) ret *= base, ret %= mod;
        base *= base, base %= mod;
        y >>= 1;
    }
    return ret;
}
int main()
{
    ll n;
    scanf("%lld", &n);
    ll ans;
    if(n == 1) ans = 0LL;
    else if(n == 2) ans = 1LL;
    else ans = (n - 2) * ksm(2, n - 1) + 1;
    printf("%lld
", ans % mod);
    return 0;
}