数学课闲的没事,Frank搞了搞事情。。。
Frank觉得4-4讲的什么玩意儿,一脸懵逼,还有伸缩变换是什么鬼?连平移都不讲的???于是Frank想到了旋转,这使Frank充满了决心qwq。
旋转。。。基本做法就是在一个圆上找一个点。。。。
Frank陷入了沉思。。。既然平移与伸缩都有公式,那么旋转是否也有呢?突然想起有个叫旋转矩阵的东西,是不是向量与旋转矩阵做乘法就得到新向量呢?
Frank崩溃了,于是他假装什么也不知道。
首先先从简单入手吧。。。画一个单位圆,设圆上的某点P(x,y),根据三角函数的知识,显然x=cosθ,y=sinθ,逆时针旋转一个角度α,即x=cos(θ+α),y=sin(θ+α),展开。。。。
嘿嘿嘿,好像看出端倪来了,于是Frank就大胆的拓展到了任意点。
而且,貌似可以简化一下,直接把点设成向量的形式,这样的话绕一个点旋转也不怕了233.
设P(x,y)为平面内任意一点,则OP即为一个从原点到P的向量,坐标也是(x,y)。设r=sqrt(x^2+y^2),显然x=rcosθ,y=rsinθ,逆时针旋转一个角度α,则。。。。。(同上)。把式子写成矩阵乘法的形式,则旋转矩阵就是。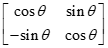
Emmmm,看起来好熟悉啊qwq,但好像负号加错位置了qwq。
上网一查才知道, Frank原来写的是行向量,但是网上是列向量。。。
不管怎样,Frank这次丢人丢大了,他还在同学面前炫耀结果被嘲讽:你知道什么是仿射变换吗?你知道什么是高斯消元吗?你知道什么是容斥原理吗?……
结果,Frank就盯着这个所谓的“旋转矩阵”,怵了半天,心便飘往幻想乡去了。。。(数学真可怕,还是东方好)