作业文件
在本次练习,第一节我们将实现异常检测算法,并把它应用到检测网络故障服务器上。在第二部分,我们将使用协同过滤来构建电影推荐系统。
1. 异常检测
在这节练习,我们将实现一个异常检测算法来检测服务器电脑异常行为。特征衡量的是每个服务器的吞吐量和延迟。当服务器运行的时候,我们收集到了m=307个样本。因此就有了一个无标签的数据集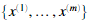 。我们假定大多数的样本都是正常的(没有异常的)。但是可能有一些异常样本。
。我们假定大多数的样本都是正常的(没有异常的)。但是可能有一些异常样本。
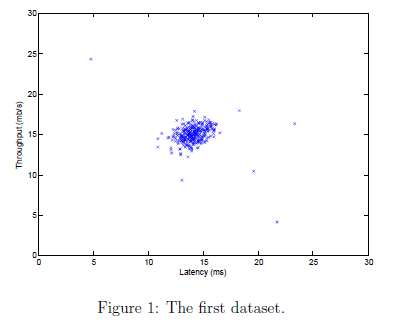
我们将使用高斯模型来检测我们数据集的异常样本。我们首先从2维数据开始,允许我们进行可视化我们的算法在做什么。在这个数据集上我们将拟合高斯分布,并找到有低概率的值,可能是异样样本。之后我们可以将异常检测算法应用到有多维的大的数据集上。2D数据集如图1所示
1.1 高斯分布
为了执行异常检测,我们首先需要拟合数据集分布的模型。给定一个数据集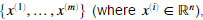 我们想要为每一个特征
我们想要为每一个特征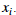 建立高斯分布。对每一个特征
建立高斯分布。对每一个特征 ,我们需要首先找到参数
,我们需要首先找到参数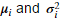 ,用于拟合第i维特征的分布。
,用于拟合第i维特征的分布。
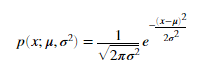
其中μ是均值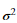 是方差。
是方差。
1.2 估计高斯的参数
我们可以估计第i个特征的参数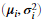 ,通过使用下面的等式。估计平均值我们可以使用:
,通过使用下面的等式。估计平均值我们可以使用:
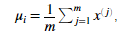
对于方差,我们可以使用
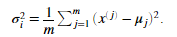
我们的任务是完成estimateGaussian.m文件内的代码,这个函数是数据矩阵X,输出n维向量mu表示每个特征平均值,和n维向量sigma2包含每个特征的方差。
注意在MATLAB中,var 函数默认使用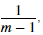 而不是
而不是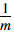 当计算
当计算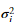 时。
时。
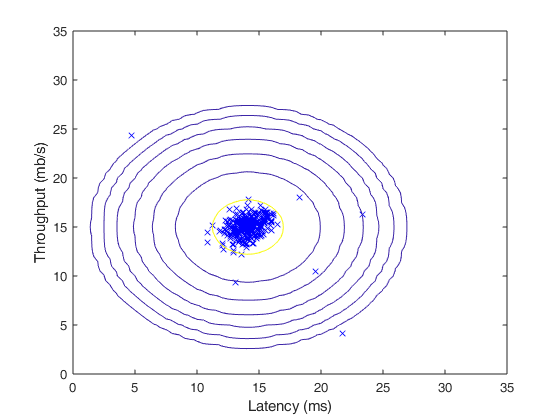
当我们完成 estimateGaussian.m内的代码时,下面代码将会可视化拟合的高斯分布的轮廓。我们画出的图应该跟图2类似。从图中我们可以看到大多数的样本在图中有很高的概率。而异样样本所在区域有底概率。
estimateGaussian.m内代码
mu = mean(X); sigma2 = mean((X-mu).^2)'; mu = mu';
1.3 选择阈值ε
我们现在获得了高斯参数,我们可以估计哪个样本有高概率,哪个样本时低概率。低概率的样本在我们的数据集中更可能是异常样本。决定哪个样本是异常的一种方式是通过交叉验证集找到阈值。在这一部分练习,我们将实现算法通过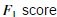 找到阈值ε。
找到阈值ε。
我们现在应该完成selectThreshold.m文件内的代码,在这里,我们将使用交叉验证集 ,其中标签等于1表示是异常样本。y=0是正常样本。对于每个交叉验证样本,我们将计算
,其中标签等于1表示是异常样本。y=0是正常样本。对于每个交叉验证样本,我们将计算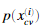 ,概率向量
,概率向量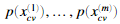 将通过pval传给selectThreshold.m。对应的标签
将通过pval传给selectThreshold.m。对应的标签 为向量 yval。
为向量 yval。
selectThreshold.m函数应该返回两个值。第一个是阈值ε,如果一个样本x的概率小于ε,那它将被认为成异样样本。函数应该同样返回F1score,告诉我们我们的阈值找的有多么好。对于不同的ε我们将计算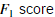
通过计算正确分类的与错误分类的数量。
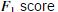 通过如下公式计算
通过如下公式计算

其中计算precision and recall通过
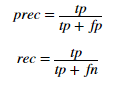
- P:精确率是针对我们预测结果而言的,它表示的是预测为正的样本中有多少是真正的正样本。那么预测为正就有两种可能了,一种就是把正类预测为正类(TP),另一种就是把负类预测为正类(FP),也就是
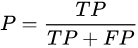
- R:而召回率是针对我们原来的样本而言的,它表示的是样本中的正例有多少被预测正确了。那也有两种可能,一种是把原来的正类预测成正类(TP),另一种就是把原来的正类预测为负类(FN)。

在selectThreshold.m中,已经有了循环计算不同的ε值,并根据F1 score选择最合适的ε。现在我们应该补全selectThreshold.m代码。通过交叉验证机计算F1 scorse。我们应该看到结果8.99e-05.
如果我们想计算一个二进制向量,有多少个0可以通过sum(v == 0)。
当我们出现selectThreshold.m内的代码我们;该看到结果如图3所示
selectThreshold.m的代码:
predictions = (pval<epsilon); tp = sum((predictions==1)&(yval==1)); fp = sum((predictions==1)&(yval==0)); fn = sum((predictions==0)&(yval==1)); prec = tp/(tp+fp); rec = tp/(tp+fn); F1 = 2*prec*rec/(prec+rec);

1.4 高维度数据集
这一部分代码将会在更复杂的数据集上执行异常检测算法。在这个数据集中,每个样本有11个特征。获得了更多服务器的属性。下面代码首先会计算高斯参数 。接着估计每个样本的概率。然后通过交叉验证集计算阈值ε,我们应该看到结果epsilon约等于1.38e-18。和117个异样样本。
。接着估计每个样本的概率。然后通过交叉验证集计算阈值ε,我们应该看到结果epsilon约等于1.38e-18。和117个异样样本。
% Loads the second dataset. You should now have the variables X, Xval, yval in your environment load('ex8data2.mat'); % Apply the same steps to the larger dataset [mu, sigma2] = estimateGaussian(X); % Training set p = multivariateGaussian(X, mu, sigma2); % Cross-validation set pval = multivariateGaussian(Xval, mu, sigma2); % Find the best threshold [epsilon, F1] = selectThreshold(yval, pval); fprintf('Best epsilon found using cross-validation: %e ', epsilon); fprintf('Best F1 on Cross Validation Set: %f ', F1); fprintf('# Outliers found: %d ', sum(p < epsilon));
2 推荐系统
在这一节练习,我们将使用协同过滤算法应用到电影评分的数据集上。电影评分的范围为1到5。数据集有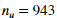 个用户,和
个用户,和 个电影。我们将实现 cofiCostFunc.m函数计算协同过滤的目标函数和梯度。在实现目标函数和梯度后,我们将使用 fmincg.m来学习协同过滤的参数。
个电影。我们将实现 cofiCostFunc.m函数计算协同过滤的目标函数和梯度。在实现目标函数和梯度后,我们将使用 fmincg.m来学习协同过滤的参数。
2.1 电影评分数据集
这一节的代码将会从ex8_movies.mat中加载数据集。提供变量Y和R。矩阵Y(num_movies num_users matrix) 存储了从1到5的评分 。矩阵R是一个二进制矩阵,其中R(i,j)=1 ,如果j给电影i评分了画。反之R(i,j)=0.协同过滤的目标是预测用户对还没评分的电影评分。
。矩阵R是一个二进制矩阵,其中R(i,j)=1 ,如果j给电影i评分了画。反之R(i,j)=0.协同过滤的目标是预测用户对还没评分的电影评分。
下面代码计算了第一个电影 (Toy Story)的平均分。
load('ex8_movies.mat'); Y is a 1682 x 943 matrix, containing ratings (1 - 5) of 1682 movies on 943 users R is a 1682 x 943 matrix, where R(i,j) = 1 if and only if user j gave a rating to movie i % From the matrix, we can compute statistics like average rating. fprintf('Average rating for movie 1 (Toy Story): %f / 5 ', mean(Y(1, R(1, :))));
我们可以可视化评分矩阵通过把他画出来
imagesc(Y); ylabel('Movies'); xlabel('Users');
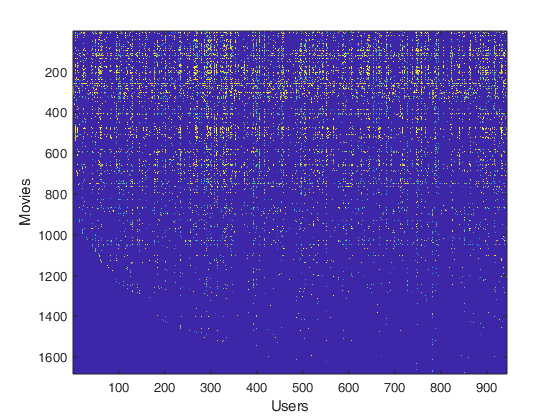
第i行对应第i个电影的特征向量。第j行对应第j个用户的参数向量。 都是n维向量。在这节练习我们使用n=100。即有100个特征。
都是n维向量。在这节练习我们使用n=100。即有100个特征。
2.2 协同过滤算法
现在我们开始实现协同过滤算法。我们首先实现代价函数。电影推荐系统中的系统过滤算法的参数是向量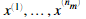 与
与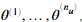 模型是通过用户j预测电影i的评分。
模型是通过用户j预测电影i的评分。 。给定一个用户已经对一些电影评分的数据集。我们希望得到参数
。给定一个用户已经对一些电影评分的数据集。我们希望得到参数 。产生最好的拟合。
。产生最好的拟合。
我们将完成cofiCostFunc.m内的代码来计算协同过滤的代价函数和梯度。注意此函数的参数是X和Theta。为了现成使用最小优化器如fmincg。代价函数必须被展开成一个单独的向量 params。我们在神经网络中也曾这样做过。
2.2.1 协同过滤的代价函数
为正则化的代价函数如下

我们应该完成cofiCostFunc.m 内的代码,并完成代价值J,注意我们需要计算代用户j和电影i的代价值,当且仅当 。当我们完成这个函数后,我们应该看到输出22.22
。当我们完成这个函数后,我们应该看到输出22.22
cofiCostFunc.m代码
J = 1/2*sum(sum(((X*Theta'-Y).*R).^2));
注意我们可是用R矩阵将需要选择项设为0,比如R.*M 可以对每个元素进行乘法。因为R元素的值只有0和1.因此R与M做点乘,结果只有R元素的值为0,M元素的值才为0.
2.2.2 协同过滤算法的梯度
现在我们应该实现写过过滤算法梯度。我们应该完成cofiCostFunc.m内代码,返回变量X_grad和Theta_grad。计算公式如下
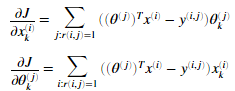
当我们完成后,梯度检测将会检测我们的梯度。如果梯度正确我们应该看到产生与梯度检测相近的结果。
定义一部电影的特征向量的导数为:
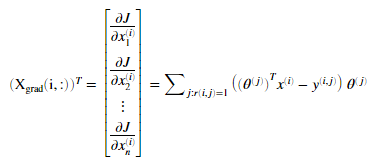
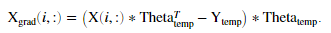
cofiCostFunc.m代码
J = 1/2*sum(sum(((X*Theta'-Y).*R).^2)); X_grad = ((X*Theta'-Y).*R)*Theta; Theta_grad = ((Theta*X'-Y').*R')*X;
2.2.3 正则化代价函数
正则化代价函数的定义如下:

完成 cofiCostFunc.m的代码
J = 1/2*sum(sum(((X*Theta'-Y).*R).^2)); X_grad = ((X*Theta'-Y).*R)*Theta; Theta_grad = ((Theta*X'-Y').*R')*X; J = J+lambda/2*sum(sum(X.^2)); J = J+lambda/2*sum(sum(Theta.^2));
2.2.4 正则化梯度
正则化的梯度函数如下

cofiCostFunc.m内代码
J = 1/2*sum(sum(((X*Theta'-Y).*R).^2)); X_grad = ((X*Theta'-Y).*R)*Theta; Theta_grad = ((Theta*X'-Y').*R')*X; J = J+lambda/2*sum(sum(X.^2)); J = J+lambda/2*sum(sum(Theta.^2)); X_grad = X_grad+lambda*X; Theta_grad = Theta_grad+lambda*Theta;
2.3 学习电影推荐系统
我们完成协同过滤的代价函数和梯度后,我们就可以训练我们自己的电影推荐系统。 。
% Load movvie list movieList = loadMovieList(); % Initialize my ratings my_ratings = zeros(1682, 1); % Check the file movie_idx.txt for id of each movie in our dataset % For example, Toy Story (1995) has ID 1, so to rate it "4", you can set my_ratings(1) = 4; % Or suppose did not enjoy Silence of the Lambs (1991), you can set my_ratings(98) = 2; % We have selected a few movies we liked / did not like and the ratings we gave are as follows: my_ratings(7) = 3; my_ratings(12)= 5; my_ratings(54) = 4; my_ratings(64)= 5; my_ratings(66)= 3; my_ratings(69) = 5; my_ratings(183) = 4; my_ratings(226) = 5; my_ratings(355)= 5; fprintf(' New user ratings: '); for i = 1:length(my_ratings) if my_ratings(i) > 0 fprintf('Rated %d for %s ', my_ratings(i), movieList{i}); end end
2.3.1 推荐系统
在将额外的评分信息添加到数据集中,我们就可以使用协同过滤训练我们的模型。学习参数X和Theta
% Load data load('ex8_movies.mat'); % Y is a 1682x943 matrix, containing ratings (1-5) of 1682 movies by 943 users % R is a 1682x943 matrix, where R(i,j) = 1 if and only if user j gave a rating to movie i % Add our own ratings to the data matrix Y = [my_ratings Y]; R = [(my_ratings ~= 0) R]; % Normalize Ratings [Ynorm, Ymean] = normalizeRatings(Y, R); % Useful Values num_users = size(Y, 2); num_movies = size(Y, 1); num_features = 10; % Set Initial Parameters (Theta, X) X = randn(num_movies, num_features); Theta = randn(num_users, num_features); initial_parameters = [X(:); Theta(:)]; % Set options for fmincg options = optimset('GradObj','on','MaxIter',100); % Set Regularization lambda = 10; theta = fmincg(@(t)(cofiCostFunc(t, Y, R, num_users, num_movies, num_features,lambda)), initial_parameters, options); % Unfold the returned theta back into U and W X = reshape(theta(1:num_movies*num_features), num_movies, num_features); Theta = reshape(theta(num_movies*num_features+1:end), num_users, num_features);
为了预测用户j对电影i的评分,我们需要计算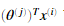 。下面代码将会计算每个用户对每部电影的评分。并显示出推荐的电影。我们可能会获得不同的预测,因为不同的随机初始化。
。下面代码将会计算每个用户对每部电影的评分。并显示出推荐的电影。我们可能会获得不同的预测,因为不同的随机初始化。
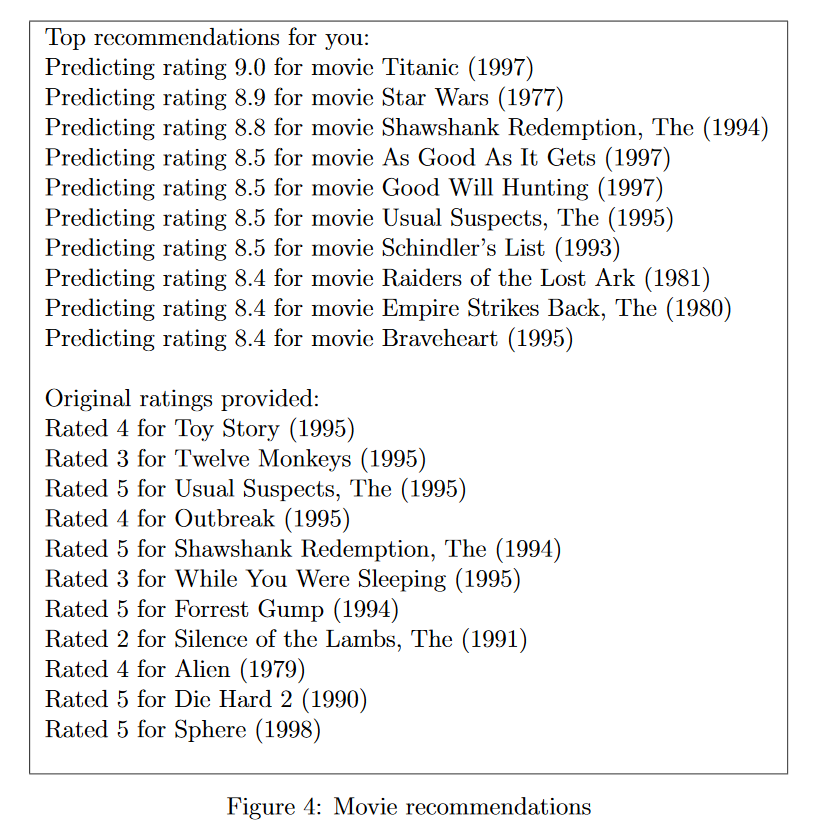
p = X * Theta'; my_predictions = p(:,1) + Ymean; movieList = loadMovieList(); [r, ix] = sort(my_predictions,'descend'); for i=1:10 j = ix(i); if i == 1 fprintf(' Top recommendations for you: '); end fprintf('Predicting rating %.1f for movie %s ', my_predictions(j), movieList{j}); end for i = 1:length(my_ratings) if i == 1 fprintf(' Original ratings provided: '); end if my_ratings(i) > 0 fprintf('Rated %d for %s ', my_ratings(i), movieList{i}); end