python求向量集合中两两向量对应的欧式距离
为了使用矩阵加速运算,因此向量集合转换成矩阵的形式,如n×m的矩阵,n为向量的个数,m为向量的维度。
方法1
def f(mat):
"""
:param mat: 矩阵n*m
:return: n个向量间两两之间对应的长度,共n*(n-1)/2个
"""
result = np.array([])
for i in range(mat.shape[0]-1):
result = np.concatenate((result,np.sqrt(np.sum((mat[i]-mat[i+1:])**2,axis=1))))
return result
依次取集合中的每个向量,计算与其他向量组成的矩阵的距离
np.sqrt(np.sum((mat[i]-mat[i+1:])**2,axis=1))
测试用例
mat = np.array([[1,2,3],[2,3,4],[0,4,2],[5,3,2]])
输出结果
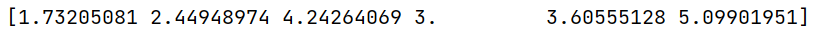
不过仍存在for循环,所以还得进一步优化
方法2
def f(mat):
"""
计算矩阵每个向量与其他向量的欧式距离
:param mat: n*m的矩阵,表示n个m维向量
:return: n*n的返回结果,对应位置值为第i与第j个向量的欧式距离(去除重复应返回n*(n-1)/2个结果)
"""
mat1 = np.expand_dims(mat, 1)
mat2 = np.expand_dims(mat, 0)
return np.sqrt(np.sum((mat1 - mat2) ** 2, axis=-1))
完全通过矩阵运算,速度会更快.
原理通过矩阵运算自动复制维度元素,当然也可以通过如下手动指定复制元素,结果相同。
可以推导下,就是在计算向量间对应元素相减的平方和,在开根号
mat1 = np.expand_dims(mat, 1).repeat(mat.shape[0],1)
mat2 = np.expand_dims(mat, 0).repeat(mat.shape[0],0)
测试用例
mat = np.array([[1,2,3],[2,3,4],[0,4,2],[5,3,2]])
输出结果
