作业文件
1. 多类分类（Multi-class Classification）
在这一部分练习，我们将会使用逻辑回归和神经网络两种方法来识别手写体数字0到9。手写体数字自动识别在今天有很 广泛的应用。这个联系将会向我们展示我们学习到的方法是如何应用到这个分类任务的。我们可以拓展我们之前实现的逻辑回归方法，并应用到一对多的分类任务。
1.1 数据集
在 ex3data1.mat文件中有给定的手写体数字的数据集，里面有5000个训练样本。.mat格式数据表示数据已保存为原生MATLAB矩阵格式，而不是text(ASCII) 格式。这些矩阵可以使用load命令直接读取到程序中去。读取后，矩阵将会出现在程序内存中。
运行下面命令读取数据：
% Load saved matrices from file load('ex3data1.mat'); % The matrices X and y will now be in your MATLAB environment
在ex3data1.mat中有5000个训练样本，每个样本是20*20像素的灰度图像，代表一个数字。每个像素是一个float类型数字，表示当前位置的灰度强度。将20*20的网格格式的像素展开成1*400的向量。所以X（5000*400的矩阵）中每一行代表一个训练样本。X的格式为：
y是一个5000*1的向量，代表了每个训练样本的输出（0到9）。因为MATLAB没有0号索引，为了更适应MATLAB的索引，我们将y中的10表示成0这个手写体数字。其他的y中的1-9就表示1-9手写数字。
1.2 可视化数据
我们将以可视化训练集的一部分子集开始。运行下面的代码，将会随机从X中选出100行数据，代表100个手写体数字。调用已经写好的displayData方法，这个方法将会将这100个数字排列成10*10的矩阵，每个元素打印一个手写体数字。你会看到如图1所示的图像。
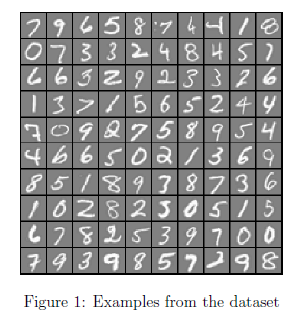
m = size(X, 1); % Randomly select 100 data points to display rand_indices = randperm(m); sel = X(rand_indices(1:100), :); displayData(sel);
1.3 矢量化逻辑回归
你将会使用一对多的逻辑回归模型来建立多类分类器。因为有10个类型数字，所以你需要训练10个逻辑回归分类器，为了使训练更有效，确保代码矢量化使非常有必要的。在这一节，我们将会实现逻辑回归的矢量化版本，因此我们就不必要使用循环。
1.3.1 矢量化代价函数（cost function）
cost funtion：
hypothesis function为：
sigmoid function为：
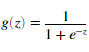
可以证明我们可以使用矩阵乘法来更快的计算代价函数，可以参考X和theta的矩阵图：
我们可以证明如果a与b都是向量的话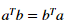 
，所以我们可以计算
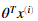的乘积计算我们的每一个样本。并且仅仅使用一样代码。
我们的任务是在lrCostFunction.m文件中填写我们的代码，正确表示代价函数。并且应该建立矢量化的代价函数，所以代码中不应该有循环。
1.3.2 矢量化梯度
在逻辑回归中梯度表示是：
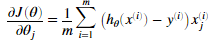
对于所有的theta的偏导数：
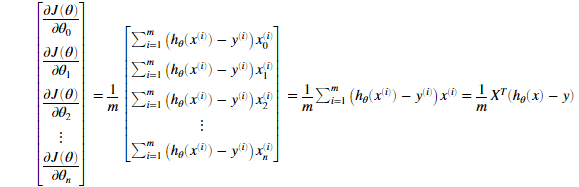
其中
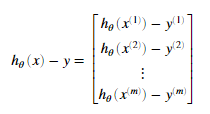
需要注意到xi是一个矢量，而
是一个标量（单个数字），为了更好的理解偏导数的最后一步，我们令
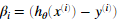并且观察下图，
即β需要与X的对应列做点乘，如对于thtea1的偏导，β需要与X的第1列做点乘。同理对于thtea2的偏导，β需要与X的第2列做点乘。
通过上面的表达式，我们可以看到我们可以通过矢量化，而允许我们计算偏导数不需要循环。
我们需要在lrCostFunction.m中填写代码，完成梯度计算。
lrCostFunction.m中的代码为：
J = (1/m)*sum(-y.*log(1./(1+exp(-X*theta)))-(1-y)*log(1-(1./(1+exp(-X*theta)))))+lambda/(2*m)*sum(theta(2:m).^2); grad = (1/m)*(sum(X.*(1./(1+exp(-X*theta))-y)))'
1.3.3 矢量化正则化逻辑回归
在完成矢量化的逻辑回归模型后，我们需要为逻辑回归进行正则化。正则化逻辑回归定义为：
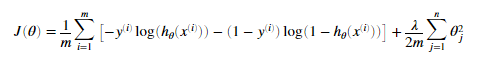
我们需要注意，theta0不需要正则化，因此对应的theta的偏导数为：
现在我们需要完善lrCostFunction.m中的代码，加上正则化。
lrCostFunction.m中的代码修改为：
J = (1/m)*sum(-y.*log(1./(1+exp(-X*theta)))-(1-y).*log(1-1./(1+exp(-X*theta))))+lambda/(2*m)*sum(theta(2:size(theta)).^2); grad = ((1/m)*sum((1./(1+exp(-X*theta))-y).*X))'; grad(2:size(theta)) = grad(2:size(theta))+lambda/m*theta(2:size(theta));
1.4 一对多的分类
在这一部分，我们将会通过训练的多个正则化的逻辑回归分类器，实现一对多的分类。每个分类器可以识别一种字体。
我们需要完成 oneVsAll.m文件中代码来为每个类训练一个分类器。我们应该返回所有分类器的参数，以一个矩阵的形式
，每一行代表一个分类器的参数。我们可以使用循环来分别训练每一个分类器。
我们需要注意，y中的10代表手写字体数字0。同时对于逻辑回归模型的训练集，y的取值应该是0或1，分别代表是不是符合预期结果。如对于识别数字7的分类器，对于训练样本x，如果y是0表示x不是数字7，如果y是1表示x是数字7。这里指的y是0或1针对的是训练集，而不是需要预测的数据。对于预测的数据分类器输出的结果介于0到1之间。
对于此回归模型，因为我们样本有10类，我训练相应的类时可以使用逻辑数组，如训练1的分类器可以使用y==1，判断y的每一元素是不是等于1并返回与y长度相同的逻辑数组。
举例：
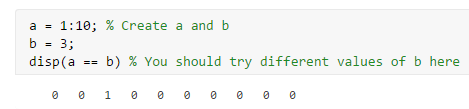
同时我们将会使用 fmincg方法训练我们分类器，求得theta。在oneVsAll.m文件中完善我们的代码完成一对多分类器，并返回每个分类器的参数，用一个矩阵表示。
oneVsAll.m中填写代码：
for i = 1:num_labels
options = optimset('GradObj', 'on', 'MaxIter', 50);
all_theta(i,:) = fmincg (@(t)(lrCostFunction(t, X, (y == i), lambda)),zeros(n + 1, 1), options);
end
1.4.1 一对多分类预测
在训练我们的一对多分类器之后我们现在可以使用我们的分类器来预测手写体数字了。对于每个输入的样本，我们应该使用所有的分类器来预测这个样本的是每个数字的概率。然后选择概率最高的数字作为输出。
我们现在应该完成predictOneVsAll.m中的代码，来使用一对多分类器预测结果。如果我们完成，运行下面代码我们将会看到我们分类器的精度大约是94.9%
predictOneVsAll.m中的代码：
[M,p] = max(1./(1+exp(-X*all_theta')),[],2);
2. 神经网络
之前的练习我们已经实现了多类逻辑回归模型来识别手写体数字，然而逻辑回归预测复杂的情况，因为它只是线性分类器。（我们添加更多的特征给逻辑回归，比如多项式特征，但是训练起来太太昂贵了）。在这一部分的练习，我们将会实现神经网络识来识别手写体数字，使用与之前相同的训练集。神经网络可以形成非线性假设来表示复杂的模型。
这周我们使用作业已经训练好的神经网络参数。我们的目标是实现前反馈传播算法来进行预测。下一周我们我们将自己实现后传播算法来学习神经网络参数。
2.1 模型表示
我们的神经网络表示为图2，它有3层，一个输入层，一个隐藏层，和一个输出层。因为每个图的大小是20*20所以输入层有400个单元（不包括1个额外的偏置单元）。
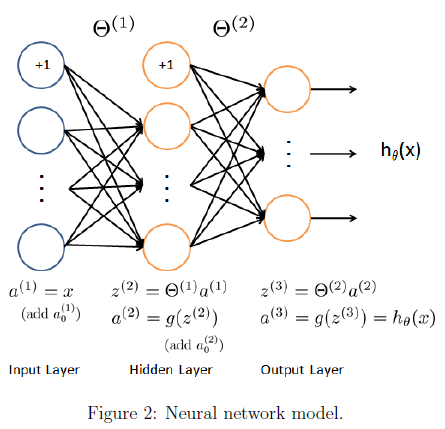
作业提供了神经网络的参数theta1与theta2。theta1的第二维的大小为第二层神经网络的单元数的个数（25）。theta2的第二维的大小为输出层的单元数的个数（10）。
2.2 前反馈传播与预测
现在我们需要实现神经网络的前反馈传播。我们需要在predict.m 中完成我们的代码，对于一个样本，我们应该预测其属于每个数字的概率。
注意：我们应该对每一层值增添一个偏置值1。
如果我们完成predict.m ，运行下面代码我们会看到此模型的预测精度大约为97.5%
X = [ones(m,1),X]; a2 = 1./(1+exp(-X*Theta1')); a2 = [ones(m,1),a2]; a3 = 1./(1+exp(-a2*Theta2')); [M,p] = max(a3,[],2);