作业文件:
1. 正则化线性回归
在本次练习的前半部分,我们将会正则化的线性回归模型来利用水库中水位的变化预测流出大坝的水量,后半部分我们对调试的学习算法进行了诊断,并检查了偏差和方差的影响。
1.1 可视化数据集
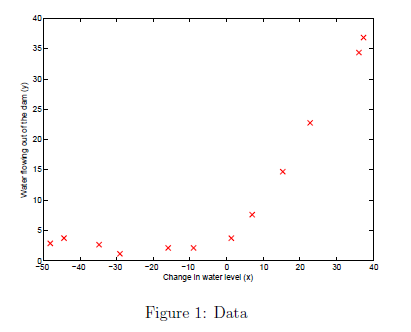
x表示水位变化,y表示水流量。整个数据集分成三个部分
- 模型的训练集,用来从X,y中学习参数。
- 交叉验证集,从Xval, yval中决定正则化参数
- 测试集,用来预测的样本,从数据集为 Xtest, ytest。
绘制的图像如图1
1.2 正则化线性回归的代价函数。
代价函数如下:

lambda是正则化参数。注意我们不应该正则化theta0,因为其代表偏置值。
在linearRegCostFunction.m文件中完成代码。对于theta初始化为[1;1].我们的输出值应该为303.993
linearRegCostFunction.m内代码:
J = 1/2/m*sum((X*theta-y).^2)+lambda/2/m*sum(theta(2:end).^2);
1.3 正则化线性回归梯度
正则化的梯度表示为:

在 linearRegCostFunction.m中添加计算梯度的代码,对于theta初始化为[1;1],我们应该看到结果
梯度值为[-15.30; 598.250]
linearRegCostFunction.m文件中代码:
J = 1/2/m*sum((X*theta-y).^2)+lambda/2/m*sum(theta(2:end).^2); grad = 1/m*(X'*(X*theta-y)); grad(2:end) = grad(2:end)+lambda/m*theta(2:end);
1.4 拟合线性回归
我们将使用 fmincg优化器来求解参数值。将lambda的值设置为0,因为只有两个参数,不会有过度拟合情况。增大lambda的值只会惩罚theta的值。用求解的参数值绘图如图2所示。

如图所示可视化最佳拟合是一种可能的方式调试学习算法。但是可视化数据和模型通常不是容易的。下面部分我们将实现一个函数来产生学习曲线,来帮助我们调试我们的学习算法,即使我们的数据不容易可视化。
2. 偏差和方差
在机器学习中一个重要的概念是方差偏差的权衡。有高偏差的模型一般比较简单不够拟合数据。有高方差的数据一般会过度拟合训练集。在这一节我们将会在学习曲线上绘制训练与测试误差来诊断偏差和方差问题。
2.1 学习曲线
现在我们将实现代码绘制学习曲线,来帮助我们调试学习算法。我们的任务是完learningCurve.m 文件中的代码,可以返回下训练集和交叉验证集的误差向量。
绘制学习曲线我们需要获得不同大小训练集的训练误差与交叉验证误差。获得不同大小的训练集我们可以使用X(1:i,:),y(1:i),i表示训练集的大小。将这些数据给前面实现的trainLinearReg函数来获得参数theta的值。在通过theta来获得训练误差与交叉验证误差。训练误差定义为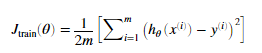
注意:训练误差是不包括正则化项的,我们可以将lambda的值设置为 0.对于训练集误差我们应该使用不同大小的训练集。对于交叉验证误差,我们应该使用所有的交叉验证数据集。
learningCurve.m 文件中代码:
for i = 1:m theta = trainLinearReg(X(1:i,:), y(1:i), lambda); error_train(i) = linearRegCostFunction(X(1:i,:), y(1:i),theta,0); error_val(i) = linearRegCostFunction(Xval, yval,theta,0); end
运行代码执行结果如图3所示

3 多项式回归
我们线性回归模型的一个问题是,模型对于数据二维太简单了,不能够好的拟合数据(有高偏差)。在这一部分练习,我们将通过添加更多特征来解决这个问题。对于多项式回归我们的假设函数是这个形式:
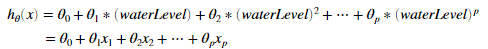
对于此的多项式回归。我们得到一个线性回归模型,其中特征是原始值的各种幂
现在我们将使用对数据集已经存在的特征x使用更高次幂来获得更多特种。我们的任务是完成polyFeatures.m的代码,通过这个函数映射m*1的原始数据矩阵X成为m*p的的数据矩阵。如第1列是原始数据的1次幂,第2列是原始数据的2次幂。
polyFeatures.m文件中代码
X_poly(:,i) = X.^i;
3.1学习多项式回归
我们使用前面完成的线性回归模型来学习多项式回归参数。
在这节练习我们将使用8阶多项式,如果直接使用结果将很差,因为如果x=40那x8次幂的特征是就是40的8次幂。因此我们需要先进行特征规范化。作业已经帮我们实现了。运行作业中的代码结果如图4图5所示
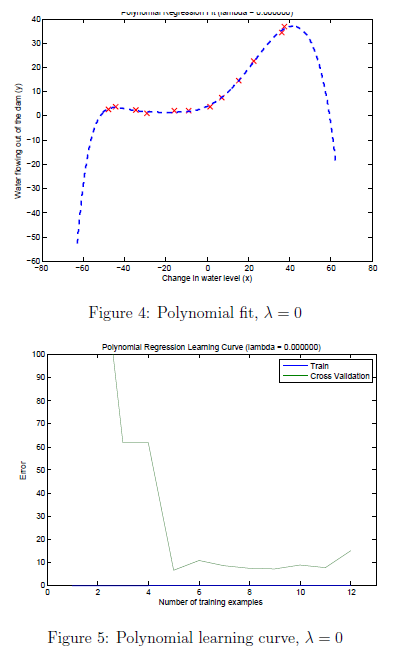
通过图4我们可以看到,多项式已经很好的拟合数据点,获得了很小的训练误差。但是此多项式太复杂了在甚至极端情况下水流量下降了。因此此多项式回归模型过度拟合训练集,因此不能很好的泛化。
3.2 可选练习:调整正则化参数
这一节我们可以观察正则化参数的影响。可以设定lambda的值为1或者100.
结果如图6图7所示
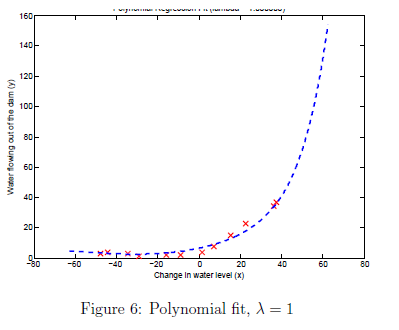
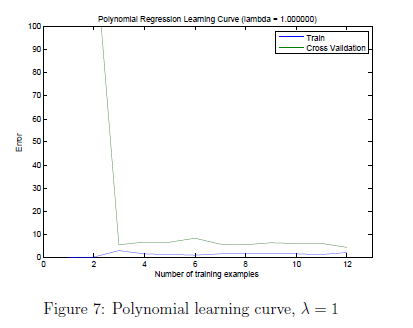
通过图7我们可以看到lambda =1 训练误差与交叉验证误差都处于一个低值。因此没有高偏差和高方差问题。对与lambda = 100如图8所示,可以看到不能很好拟合数据。

3.3 使用交叉训练集选择lambda的值
从之前练习我们可以看到lambda的值会对多项式回归模型有显著影响。
在这一节我们会实现自动选择labmbda的值的函数。具体来说,通过交叉验证集来测试那个lambda的值是最合适的。我们可以通过测试机来评估我们的模型对未知的数据的表现如何。我们的任务是完成validationCurve.m文件的代码。我们应该使用trainLinearReg函数,来使用不同的lambda的值训练模型。我们将测试的lambda的值是:{0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10}.
在完成代码后我们应该会看到如图9所示的图像。
validationCurve.m文件代码:
for i = 1:length(lambda_vec) theta = trainLinearReg(X, y, lambda_vec(i)); error_train(i) = linearRegCostFunction(X, y,theta,0); error_val(i) = linearRegCostFunction(Xval, yval,theta,0); end
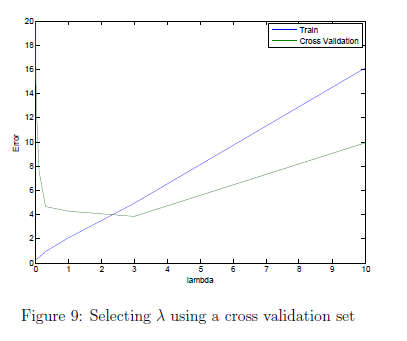
3.4 可选练习:计算测试集误差
之前我们已经计算交叉验证集误差与训练集误差,为了更好的了解模型的表现,使用测试集评估最终的模型是非常有必要的。
我们已经获得当lambda = 3时测试集误差为3.8599
theta = trainLinearReg(X_poly, y, 3);
linearRegCostFunction(X_poly_test, ytest,theta,0)