前言
索引可能大家都不陌生,在用关系型数据库时,一些频繁用作查询条件的字段我们都会去建立索引来提升查询效率。在关系型数据库中,我们一般都采用 B 树索引进行存储,所以 B 树索引也是我们接触比较多的一种索引数据结构,然而在 es 中,进行全文搜索的时候却并没有选择使用 B 树 索引,而是采用的倒排索引。本文就让我们来看看 es 中的倒排索引是如何存储和检索的吧。
为什么全文索引不使用 B+ 树进行存储
关系型数据库,如 MySQL,其选择的是 B+ 树索引,如下图就是一颗简单的的 B+ 树示例:
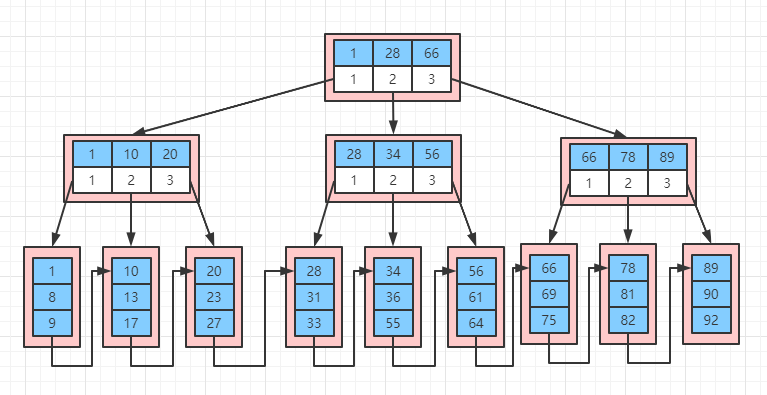
上图中蓝色的表示索引值,白色的表示指针,最底层叶子节点除了存储索引值还会存储整条数据(InnoDB 引擎),而根节点和枝节点不会存储数据,B+ 树之所以这么设计就是为了使得根节点和枝节点能够存储更多的节点,因为搜索的时候从根节点开始搜索,每查询一个节点就是一次 IO 操作,所以一个节点能存储更多的索引值能减少磁盘 IO 次数。
如果有想更详细了解 B+ 树的,可以点击这里。
那么到这里我们就可以思考这个问题了,假如索引值本身就很大,那么 B+ 树是不是性能会急剧下降呢?答案是肯定的,因为当索引值很大的话,一个节点能存储的数据会大大减少(一个节点默认是 16kb 大小),B+ 树就会变得更深,每次查询数据所需要的 IO 次数也会更多。而且全文索引就是需要支持对大文本进行索引的,从空间上来说 B+ 树不适合作为全文索引,同时 B+ 树因为每次搜索都是从根节点开始往下搜索,所以会遵循最左匹配原则,而我们使用全文搜索时,往往不会遵循最左匹配原则,所以可能会导致索引失效。
总结起来 B+ 树不适合作为全文搜索索引主要有以下两个原因:
- 全文索引的文本字段通常会比较长,索引值本身会占用较大空间,从而会加大
B+树的深度,影响查询效率。 - 全文索引往往需要全文搜索,不遵循最左匹配原则,使用
B+树可能导致索引失效。
全文检索
在全文检索当中,我们需要对文档进行切词处理,切好之后再将切出来的词和文档进行关联,并进行索引,那么这时候我们应该如何存储关键字和文档的对应关系呢?
正排索引
可能大家都知道,在全文检索中(比如:Elasticsearch)用的是倒排索引,那么既然有倒排索引,自然就有正排索引。
正排索引又称之为前向索引(forward index)。我们以一篇文档为例,那么正排索引可以理解成他是用文档 id 作为索引关键字,同时记录了这篇文档中有哪些词(经过分词器处理),每个词出现的次数已经每个词在文档中的位置。
但是我们平常在搜索的时候,都是输入一个词然后要得到文档,所以很显然,正排索引并不适合于做这种查询,所以一般我们的全文检索用的都是倒排索引,但是倒排索引却并不适合用于聚合运算,所以其实在 es 中的聚合运算用的是正排索引。
倒排索引
倒排索引又称之为反向索引(inverted index)。和正排索引相反,倒排索引使用的是词来作为索引关键字,并同时记录了哪些文档中有这个词。
在这里我们以一个英文文档为例子,之所以选择用英文文档是因为英文分词比较简单,直接以空格进行分词即可,而中文分词相对比较复杂。
我们以 Elasticsearch 官网中下面两句话作为两位文档来分析:
Elasticsearch is the distributed search and analytics engine at the heart of the Elastic Stack.
Elasticsearch provides near real-time search and analytics for all types of data.
根据上面两句话,假设我们可以得到下面这样的一个索引结构:
| term index | term dictionary | Posting list TF |
|---|---|---|
| term 索引 | elasticsearch | [1,2] |
| term 索引 | search | [1,2] |
| term 索引 | elastic | [1] |
| term 索引 | provides | [2] |
其中:
- term index:顾名思议,这个是为
term(经过分词后的每个词) 建立的索引,也就是通过这个索引可以快速找到当前term的位置,从而找到对应的Posting list。因为在es中,会为每个字段都建立索引(默认存储在内存中),所以当我们的数据量非常大的时候,就需要能快速定位到这个词对应的索引所在的内存位置,所以就单独为每个term建立了索引,这个索引一般可以选择哈希表或者B+树进行索引存储。 - term dictionary:记录了文档中去重后的所有词(经过分词器处理)。
- Posting list TF:记录了含有当前词的文档以及当前词出现在文档的位置(偏移量),该项信息是一个数组,上面表格中为了简单只列举了文档
id,实际上这里会存储很多信息。
这时候假如我们搜索 Elasticsearch Elastic 这样的关键字,那么会经过以下步骤:
- 对输入的关键字进行分词处理,得到两个词:
elasticsearch和elastic(经过分词器之后大写字母都会转化成小写字母)。
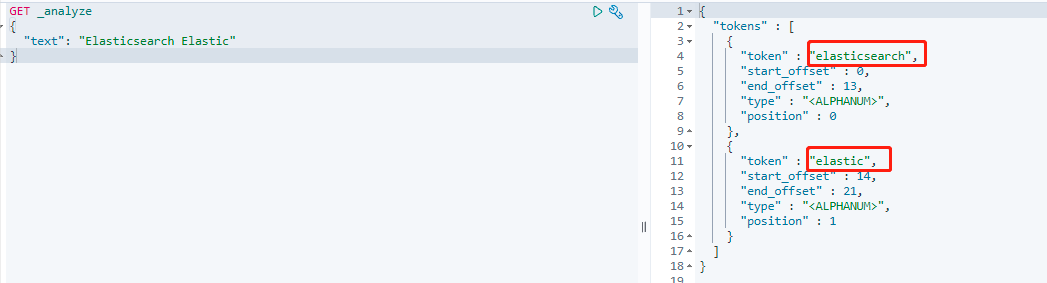
- 然后分别用这两个词进行搜索,搜索之后,发现
elasticsearch在两个文档中都有出现,而elastic只在文档一中出现。 - 最终的搜索结果就是文档一和文档二都返回,但是因为文档一两个词都命中了,所以相关度(分数)更高,于是文档一会排在文档二前面,这就是算分的过程。不过需要注意的是,实际的这种相关度分数算法不会这么简单,而是有专门的算法来计算,命中词多的并不一定会出现在前面。
倒排索引如何存储数据
知道了倒排索引的搜索过程,那么倒排索引的数据又是如何存储的呢?
回答这个问题之前我们先来看另一个问题,那就是建立索引的目的是什么?最直接的目的肯定是为了加快检索速度,而为了达到这个目的,那么在不考虑其他因素的情况下,必然是需要占用的空间越少越好,而为了减少占用空间,可能就需要压缩之后再进行存储,而压缩之后又涉及到解压缩,所以采用的压缩算法也需要能达到快速压缩和解压的目的。
FOR 压缩
FOR 压缩算法即 Frame Of Reference。这种算法比较简单,也有一定的局限性,因为其对存储的文档 id 有一定要求。
假设现在有一亿个文档,对应的文档 id 就是从 1 开始自增。假设现在关键字 elasticsearch 存在于 1000W 个文档中,而这 1000W 个文档恰好就是从 1 到 1000W,那么假如不采用任何压缩算法,直接进行存储需要占用多少空间?
int 类型占用了 4 个字节,而 1000W 这个数量级需要 2 的 24 次方,也就是说如果用二进制来存储,在不考虑符号位的情况下也需要 24 个 bit 才能存储,而因为 Posting list TF 是一个数组,所以为了能解析出数据,文档 id=1 的数据也需要用 24 个 bit 来进行存储,这样就会极大的浪费了空间。
为了解决这个问题,我们就需要使用 FOR 算法,FOR 算法并不直接存储文档 id,而是存储差值,像这种这么规律的文档 id,差值都是 1,而 1 转成二进制就可以只使用 1 个 bit 进行存储,这样就只需要 1000W 个 bit 的空间来进行存储就够了,相比较直接存储原始文档 id 的情况下,这种场景采用 FOR 算法大大减少了空间。
上面举的这个例子是比较理想的情况,然而实际上这种概率是比较小的,那我们再来看下面这一组文档 id:
1,9,15,45,68,323,457
这个数组计算差值后得到下面这个数组:
8,6,30,23,255,134
这个时候如果还是直接用普通差值的算法,虽然也能节省空间,但是却并不是最优的一种解决方案,那么这个时候有没有一种更高效的方法来进行存储呢?
我们观察下这个差值数组,发现这个数组可以进一步拆分成两组:
- [8,6,30,23]:这一组最大值为
30,只需要5个比特就能进行存储。 - [255,134]:这一组最大值为
255,需要8个比特就能存储。
这么拆分之后,原始数据需要用 32*7=224 个比特(原始数据直接用 int 存储),普通差值需要 8*6=48 个比特,而经过分组差值拆分之后只需要 5*4+8*2=36 个比特,进一步压缩了空间,这种优势随着数据量的增加会更加明显。
但是不管采用哪种方案都有一个问题,那就是进行差值或者拆分之后,怎么还原数据,解压的时候怎么知道差值数组内的元素占用空间大小?
所以对每一个数据,还需要一块一个字节的空间大小来存储当前数组内元素占用的比特数,所以分组并不是越细越好,假如对每一个差值元素都单独存储,那么反而会比不分组更浪费空间,反之,如果每个分组内的元素足够多,那么存储占用空间的这一个字节反带来的影响就会更小或者忽略不计。
RBM 压缩
上面例子中介绍的差值都不会大相径庭,那么假如我们差值计算之后得到的数组,其每个元素差别都很大呢?比如说下面这个文档 id 数组:
1000,62101,131385,132052,191173,196658
这个数组大家可以去计算一下差值,计算之后会发现一个大一个小,两个差值之间差距很大,所以这种方式就不适合于用 FOR 压缩,所以我们就需要有另外的压缩算法来提升效率,这就是 RBM 压缩。
RBM 压缩算法即 Roaring Bitmap,是在 2016 年由 S. Chambi、D. Lemire、O. Kaser 等人在论文《Better bitmap performance with Roaring bitmaps》与《Consistently faster and smaller compressed bitmaps with Roaring》中提出来的。
RBM 压缩算法的核心思想是:将 32 位无符号整数按照高 16 位进行划分容器,即最多可能有 65536 个 container。因为 65536 实际上就是 2 的 16 次方,而一个无符号 int 类型正好是需要 32 位进行存储,划分为高低位正好两边都是 16 位,也就是最多 65536 个。
划分之后根据高 16 位去找 container(比如高 16 位计算的结果是 1 就去找 container_1,2 就去找 container_2,依次类推),找到之后如果发现容器不存在,那么就会新建一个容器,并且把低 16 位存入容器内,如果容器存在,就直接将低 16 位存入容器。
这样就会出现一个现象:那就是容器最多有 65536 个,而每个容器内的元素也恰好最多是 65536 个元素。
也就是上面的数组经过计算就会得到以下容器(container_1 没有元素):

如果说大家觉得上面的高低 16 位不好理解,那么可以这么理解,我们把数组中的元素全部除以 65536,对其取模,每得到一个模就创建一个容器,而其余数就放入对应的模所对应的容器中。因为一个 int 类型就是 2 的 32 次方,正好是 65536 的平方。
经过运算之后得到容器,那么容器中的元素又该如何进行存储呢?可以选择直接存储,也可以选择其他更高效的存储方式。在 RBM 算法中,总共有三种容器类型,分别采用不同的方法来存储容器中的元素:
- ArrayContainer
ArrayContainer 采用 short 数组来进行存储,因为每个容器中的元素最大值就是 65535,采用 2 个字节进行存储。这种存储方式的特点是随着元素个数的增多,所需空间会一直增大。
- BitmapContainer
BitmapContainer 采用位图的方式进行存储,也就是固定创建一个 65536 长度的容器,容器中每个元素只用一个比特进行存储,某一个位置有元素则存储 1,没有元素则存储为 0。这种存储方式的特点是空间固定就是占用 65536 个比特,也就是大小固定为 8kb。
- RunContainer
RunContainer 比较特殊,在特定场景下会使用,比如文档 id 从 1-100 是连续的,那么采用这种容器就可以直接存 1,99,表示 1 后面有 99 个连续的数字,再比如 1,2,3,4,5,6,10,11,12,13 可以被压缩为 1,5,10,3,表示 1 后面有 5 个连续数字,10 后面有 3 个连续数字。
至于每次存储采用什么容器,需要进行一下判定,比如 ArrayContainer,当存储的元素少于 4096 个时,他会比 BitmapContainer 占用更少空间,而当大于 4096 个元素时,采用 ArrayContainer 所需要的空间就会大于 8kb,那么采用 BitmapContainer 就会占用更少空间。
倒排索引如何存储
前面我们讲了 es 中的倒排索引采用的是什么压缩算法进行压缩,那么压缩之后的数据是如何落地到磁盘的呢?采用的是什么数据结构呢?
字典树(Tria Tree)
字典树又称之为前缀树(Prefix Tree),是一种哈希树的变种,可以用于搜索时的自动补全、拼写检查、最长前缀匹配等。
字典树有以下三个特点:
- 根节点不包含字符,除根节点外的其余每个节点都只包含一个字符。
- 从根节点到某一节点,将路径上经过的所有字符连接起来,即为该节点对应的字符串。
- 每个节点的所有子节点包含的字符都不相同。
下图所示就是在数据结构网站上依次输入以下单词(AFGCC、AFG、ABP、TAGCC)后生成的一颗字典树:

上图中可以发现根节点没有字母,除了根节点之外其余节点有白色和绿色两种颜色之分,这两种颜色的节点有什么区别呢?
绿色的节点表示当前节点是一个 Final 节点,也就是说当前节点是某一个单词的结束节点,搜索的时候当发现末尾节点是一个 Final 节点则表示当前字母存在,否则表示不存在。
比如我现在搜索 ABP,从根节点往下找的时候,最后发现 P 是一个 Final 节点,那就表示当前树中存在字符串 ABP,如果搜索 AFGC,虽然也能找到这些字母,但是 C 并不是一个 Final 节点,所以字符串 AFGC 并不存在。
不过字典树存在一个问题,上图中就可以体现出来,比如第二列中的后缀 FGCC 和 第三列中的 GCC 其实最后三个字符是重复的,但是这些重复的字符串都单独存储了,并没有被复用,也就是说字典树没有解决后缀共用问题,只解决了前缀共用(这也是字典树又被称之为前缀树的原因)。当数据量达到一定级别的时候,只共享前缀不共享后缀也会带来很多空间的浪费,那么如何来解决这个问题呢?
FST
要解决上面字典树的缺陷其实思路也很简单,就是除了利用字符串的前缀,同时也将相同的后缀进行利用,这就是 FST,在了解 FST 之前,我们先了解另一个概念,那就是 FSM,即:Finite State Transducer。
FSM
FSM,即 Finite State Machine,翻译为:有限状态机。如果大家有了解过设计模式中的状态模式的话,那么应该会对状态机有一定了解。有限状态机顾明思议就是状态可以全部被列举出来,然后随着不同的操作在不同的状态之间流程。
如下图所示就是一个简易的有限状态机(假设一个人一天做的事就是下面的所有状态,那么状态之间可以切换流转,下图中的数字表示状态的转换条件):
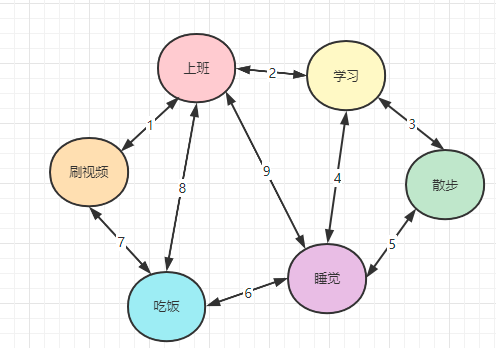
有限状态机主要有以下两个特点:
- 状态是有限的,可以被全部列举出来。
- 状态与状态之间可以流转。
而我们今天所需要学习的 FST,其实就是通过 FSM 演化而来。
继续回到我们上面的那颗字典树,那么假如现在我们换成 FST 来存储,会得到如下的数据结构:

上面这幅图是怎么得到的呢?字母后的数字又代表了什么含义呢?有些节点有数字,有些是空白又有什么区别呢?这幅图又是如何区分 Final 节点呢?接下来我们就一步步来来构建一个 FST。
构建 FST
首先我们知道,既然现在讲的是存储索引,所以除了 key 之外自然得有 value,否则是没有意义的,所以上图中其实字母就代表了索引关键字,也就是 key,而后面的数字代表了存储的文档 id(最终会转换成二进制存储),然而这个 每个数字代表的 id 又可能是不完整的,这个我们下面会解释原因。
- 首先我们收到第一个存储索引的的键值对
AFGCC/5,得到如下图:

上图中红色代表开始节点,深灰色代表结束节点,加粗的线条代表其后面的节点是一个 Final 节点。这里有一个问题,那就是 5 为什么要存储在第一条线(没有存储数字的线上实际上是一个 null 值),实际上我存储在后面的任意一条线都可以,因为最终搜索的时候会把整条线路上所有的数字加起来得到最终的 value,这也就是上面我为什么说每一条线上的 value 可能是不完整的,因为一个 value 可能会被拆成好几个数字相加,并且存储在不同的线上。
首先这个 5 为什么要存储在第一段其实是为了提高复用率,因为越往前复用的机会可能就会越大。
- 继续存储第二个索引键值对
AFG/10,这时候得到下图:

这时候我们发现,G 后面的节点存储了一个 5,其他线段上并没有存储数字,这是为什么呢?因为 10=5+5,而前面第一段已经存储了一个 5,后面一个 5 存储在任何一段线上都会影响到我们的第一个键值对 AFGCC/5,所以这时候就只能把他存储在当前索引 key 所对应的 Final 节点上(源码中有一个属性 output),因为搜索的时候,如果路过不属于自己的 Final 节点上的 value,是不会相加的,所以当我们搜索第一个索引值 AFGCC 的时候,是不会把 G 后面的 Final 节点中的 value 取出来相加的。
- 接下来继续存储第三个索引键值对
ABP/2,这时候得到下图:
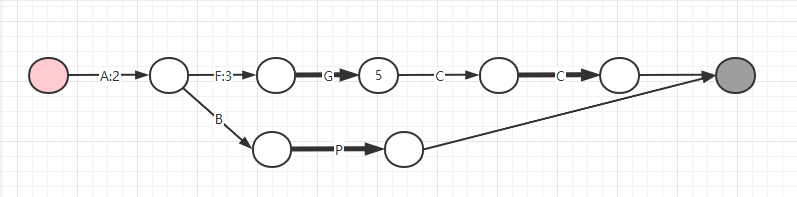
这时候因为 ABP 字符串和前面共用了 A,而 A 对应的 value 是 5,已经比 2 大了,所以只要共用 A,那么是无论如何也无法存储成功的,所以就只能把第一个节点 5 拆成 2+3,原先 A 的位置存储 2,那么后面的 3 遵循前面的原则,越靠前存储复用的概率越大,所以存在第二段线也就是字符 F 对应的位置,这时候就都满足条件了。
- 最后我们来存储最后一个索引键值对
TAGCC/6,最终得到如下图:
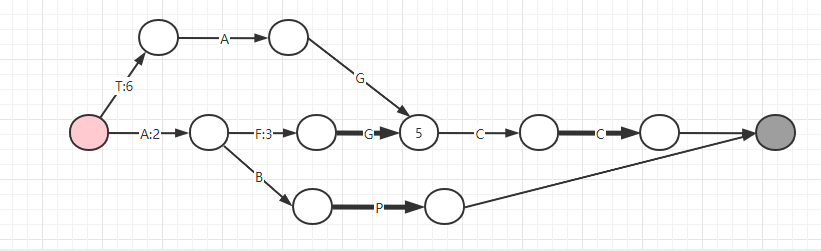
这时候因为 GCC 这个后缀和前面是共用的,而恰好 GCC 之后的线上都没有存储 value,所以直接把这个 6 存储在第一段线即可,注意,如果这里再次发生冲突,那么就需要再次重新分配每一段 value,到这里我们就得到和上图中网站内生成的一样的 FST 了。
总结
本文主要讲解了在 Elasticsearch 中是如何利用倒排索引来进行数据检索的,并讲述了倒排索引中的 FOR 和 RBM 两种压缩算法的原理以及使用场景,最后对比了字典树(前缀树)和 FST 两种数据结构存储的区别,并最终得出了为什么 es 中选择 FST 而不是选择字典树来进行存储索引数据的原因。