Team Contests

Problem F

 

Problem Description

There are n points in a geometrical plane. If there exists a rectangle whose four vertices are among those points and every edge of the rectangle has exactly m points which are among those points, now ask how many rectangles existing in this plane could satisfy all the conditions. The edge of the rectangle should be parallel to the coordinate axes. This is a rectangle that satisfy the conditions when m=3 represented in the chart below. 

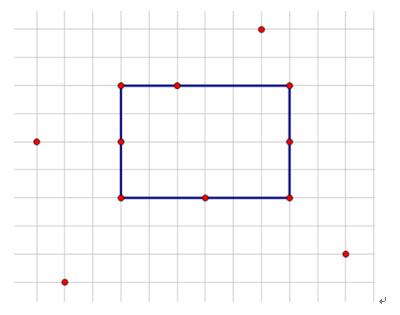
Input

First line contains T(T≤20) denoting the number of test cases.

  T cases follows for each cases: 

  First line contains two integers n,m(5≤n≤100000,m<n)

  Followed by n lines, each line contains two integers xi,yi indicates the location of the i-th point. There are no two points at the same location. (|Xi|,|Yi|≤10000000)

Output

For each case, output an integer indicate the number of rectangles that satisfy the condition.

Sample Input

1
9 2
0 0
0 3
0 6
3 0
3 3
3 6
6 0
6 3
6 6

Sample Output

4

题意是输入n和m，给出n个点，要找出一种矩形，这种矩形的四个顶点都属于给出的顶点，并且这个矩形四条边上拥有的n个点中的点的数量都是m
我的做法是把坐标先按x大小排序，再按y大小排序，得到两个数组xy, yx，然后以长度为m的段在xy中找到一条符合条件的边，这样可确定左上的点，通过二分在yx数组中查找左下的点，判断是否满足条件，以此类推找右下，右下，再返回左上，如果能返回就说明找到了一个矩形。

#include <cstdio>
#include <cstring>
#include <cmath>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 1e5 + 10;
typedef pair<int, int> pii;
#define x first
#define y second
pii xy[maxn], yx[maxn];

int main() {
    int t;
    scanf("%d", &t);
    while(t--) {
        int n, m, xx, yy;
        scanf("%d %d", &n, &m);
        for(int i = 1; i <= n; i++) {
            scanf("%d %d", &xx, &yy);
            xy[i] = pii(xx, yy);
            yx[i] = pii(yy, xx);
        }
        sort(xy + 1, xy + 1 + n);
        sort(yx + 1, yx + 1 + n);
        int l = 1, r = m;
        int ans = 0;
        pii tmp;
        while(r <= n) {
            if(xy[l].x == xy[r].x) {
                int pos, pos2, pos3;
                tmp.x = xy[l].y, tmp.y = xy[l].x;
                pos = lower_bound(yx + 1, yx + 1 + n, tmp) - (yx);
                //printf("check %d %d %d
", pos, xy[l].x, xy[r].x);
                if(yx[pos].x == yx[pos+m-1].x) {
                    tmp.x = yx[pos+m-1].y, tmp.y = yx[pos+m-1].x;
                    pos2 = lower_bound(xy + 1, xy + 1 + n, tmp) - (xy);
                    if(xy[pos2].x == xy[pos2+m-1].x) {
                        tmp.x = xy[pos2+m-1].y, tmp.y = xy[pos2+m-1].x;
                        pos3 = lower_bound(yx + 1, yx + 1 + n, tmp) - (yx);
                        if(yx[pos3].x == yx[pos3+1-m].x) {
                            ans++;
                        }
                    }
                }
            }
            l++, r++;
        }
        printf("%d
", ans);
    }
}