@
一、从高斯分布到信息矩阵
1.1 SLAM 问题概率建模
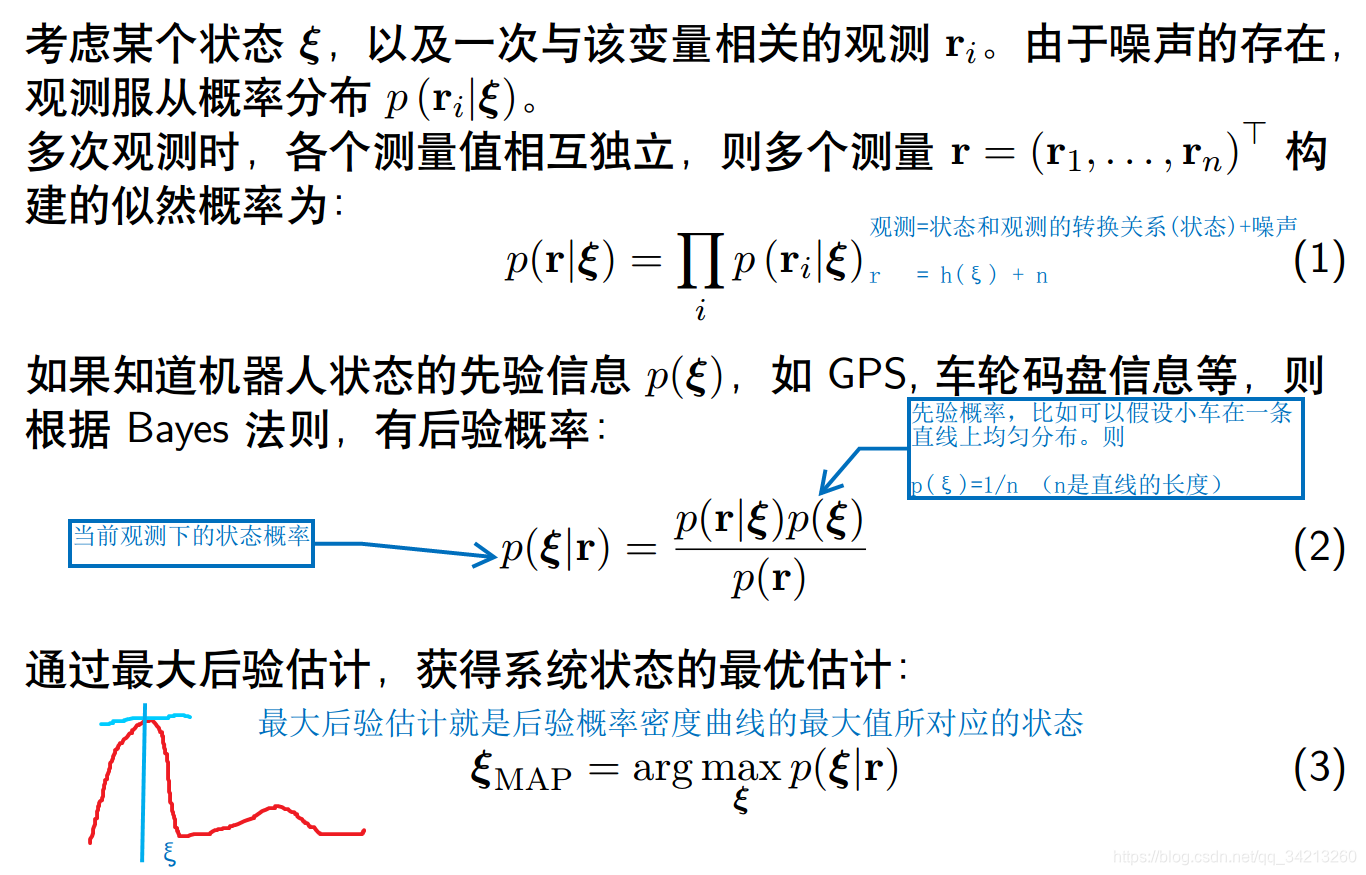
1.2 SLAM 问题求解

1.3 高斯分布和协方差矩阵
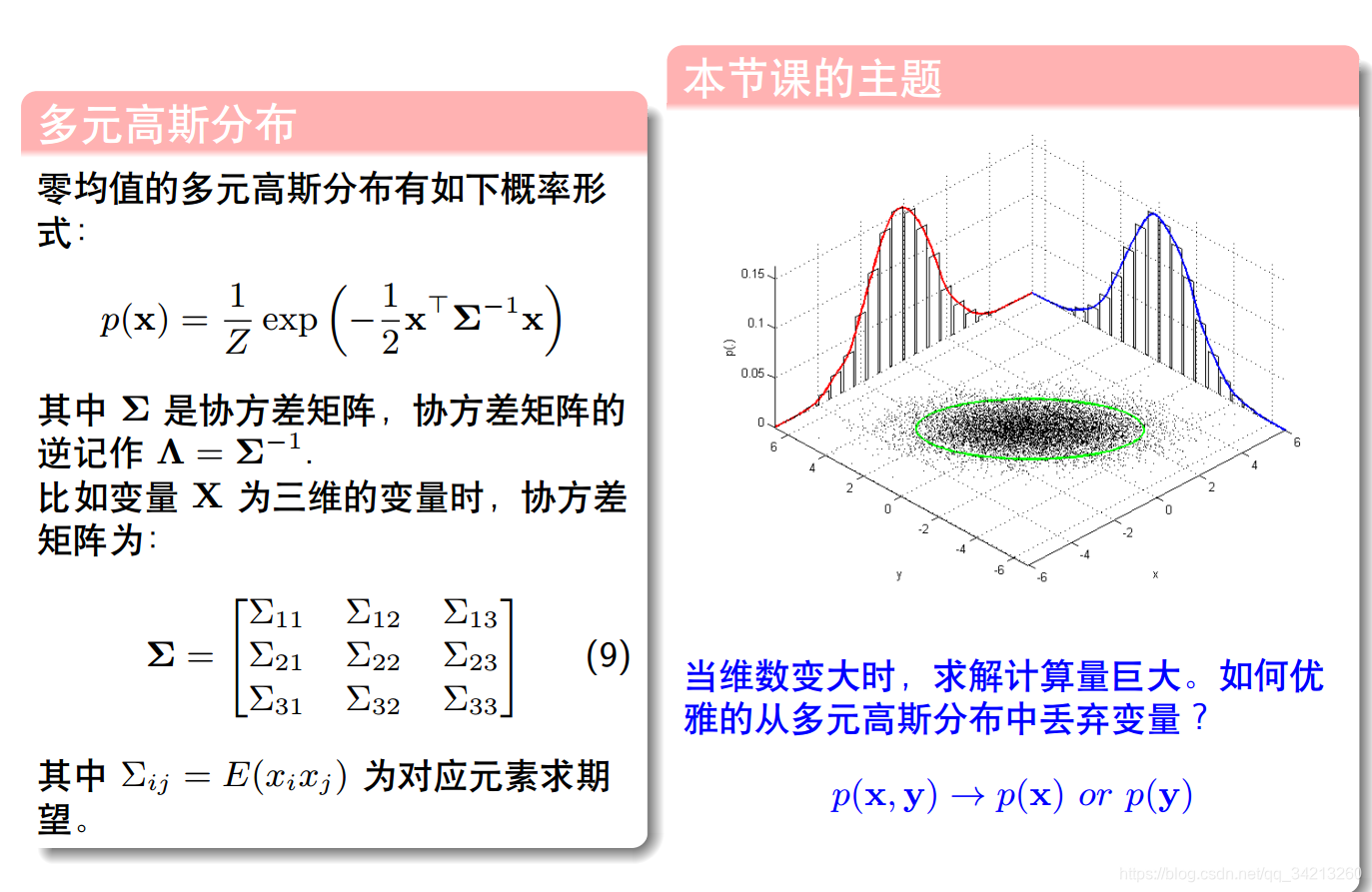 因为一般可以假设(x_{i}和 x_{j})是相互独立的:
因为一般可以假设(x_{i}和 x_{j})是相互独立的:
(Sigma_{i j}=Eleft(x_{i} x_{j}
ight)=E(x_i)E(x_j)=(x-u)^T(x-u))
1.4 样例
1.4.1 样例1







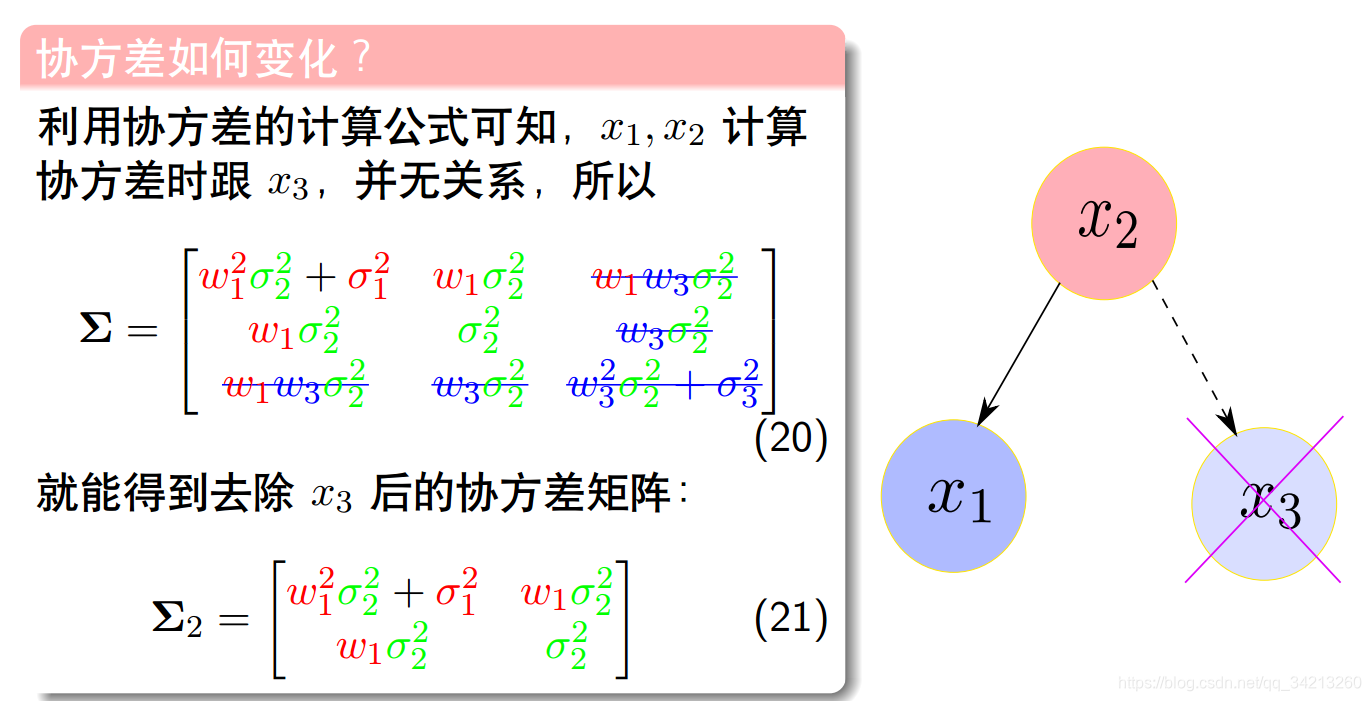
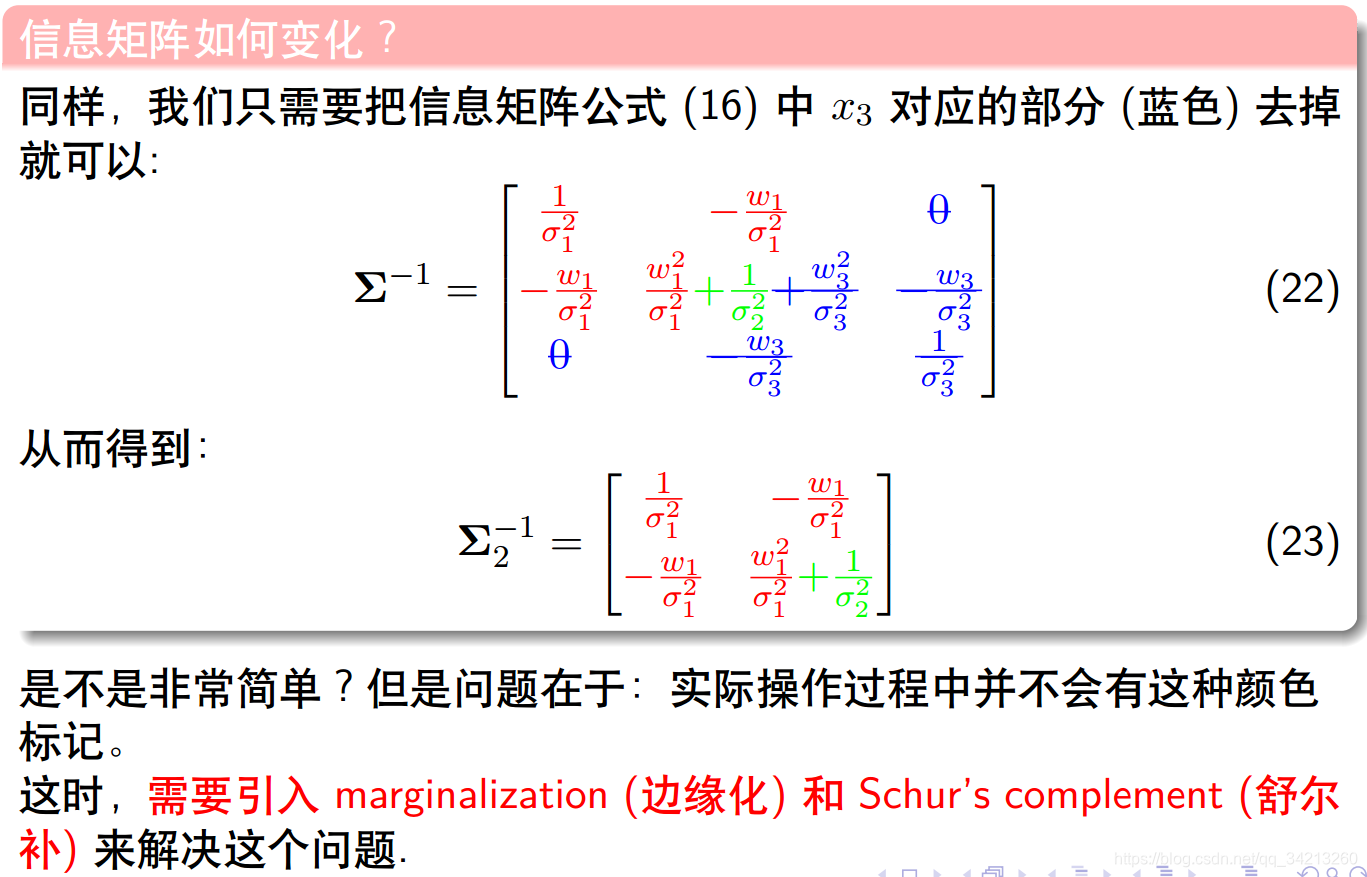 因为实际过程中是协方差矩阵里面各个值是一个数,已经没有办法单独去掉某一部分。
因为实际过程中是协方差矩阵里面各个值是一个数,已经没有办法单独去掉某一部分。
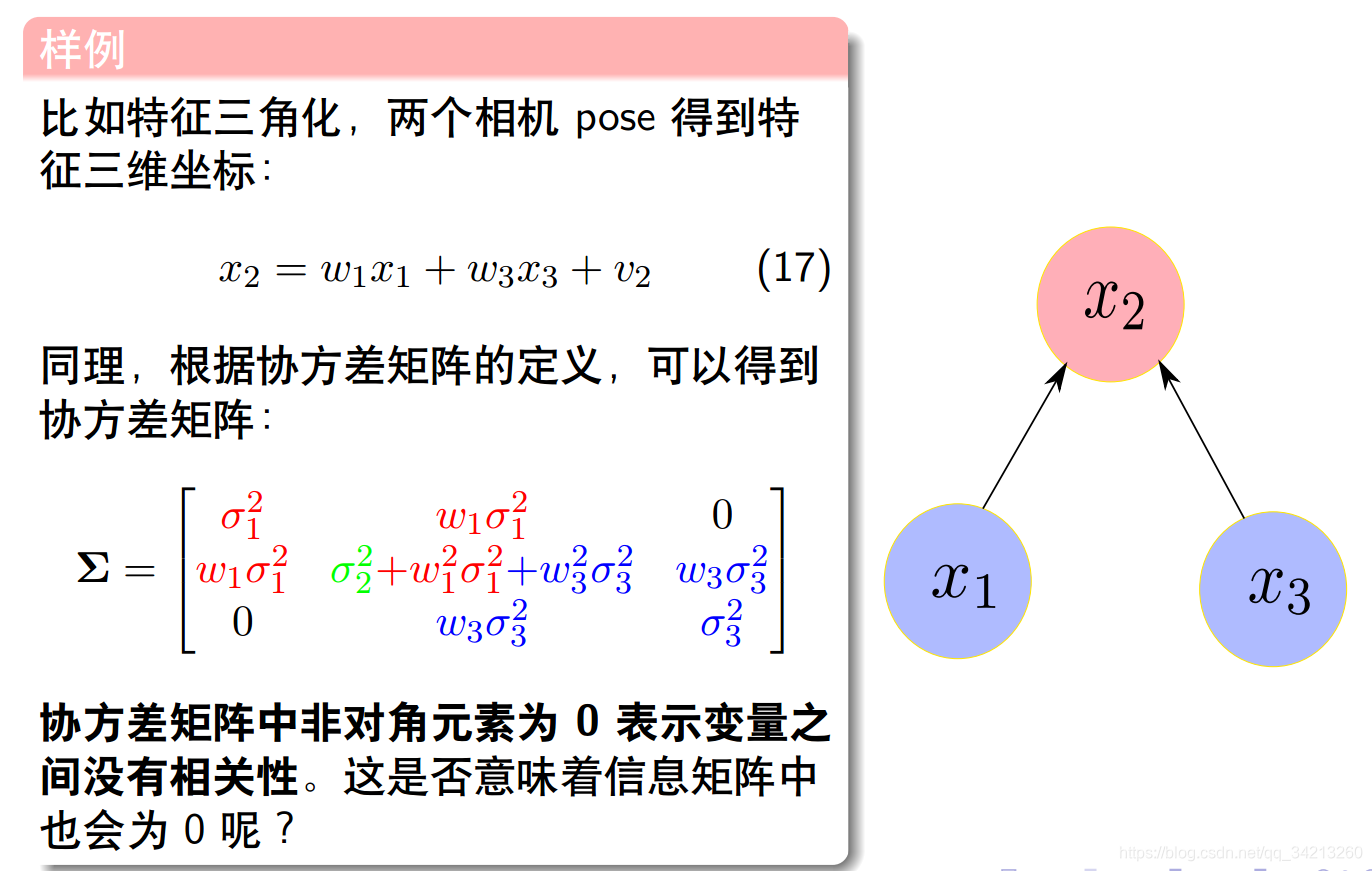
1.4.2 样例2


二、舒尔补应用:边际概率, 条件概率
2.1 舒尔补的概念
 更多定义参见:Wiki. Schur Complement.
更多定义参见:Wiki. Schur Complement.
2.2 舒尔补的来由

2.3 使用舒尔补分解的好处

2.4 舒尔补应用于多元高斯分布


2.5 关于 P(a), P(b|a) 的协方差矩阵

2.6 关于 P(a), P(b|a) 的信息矩阵


2.7 回顾样例

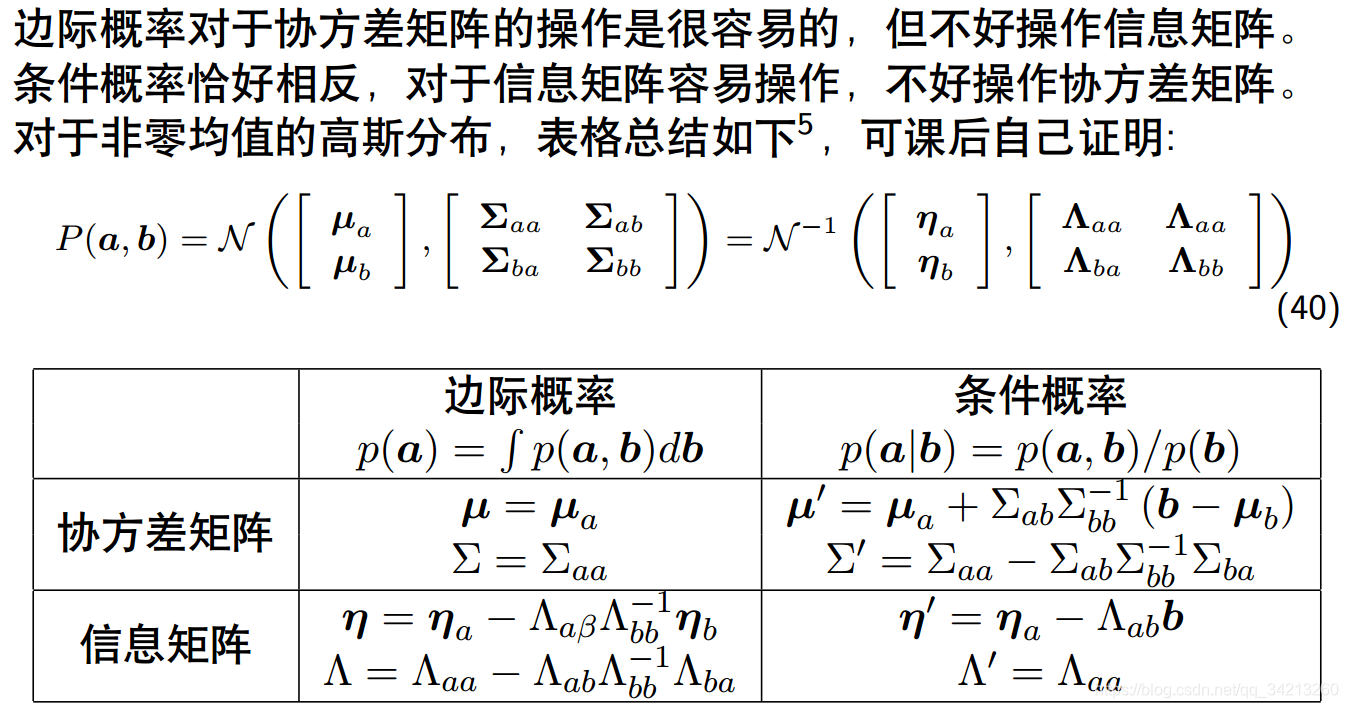
2.8 总结
三、滑动窗口算法
3.1 最小二乘用图表示
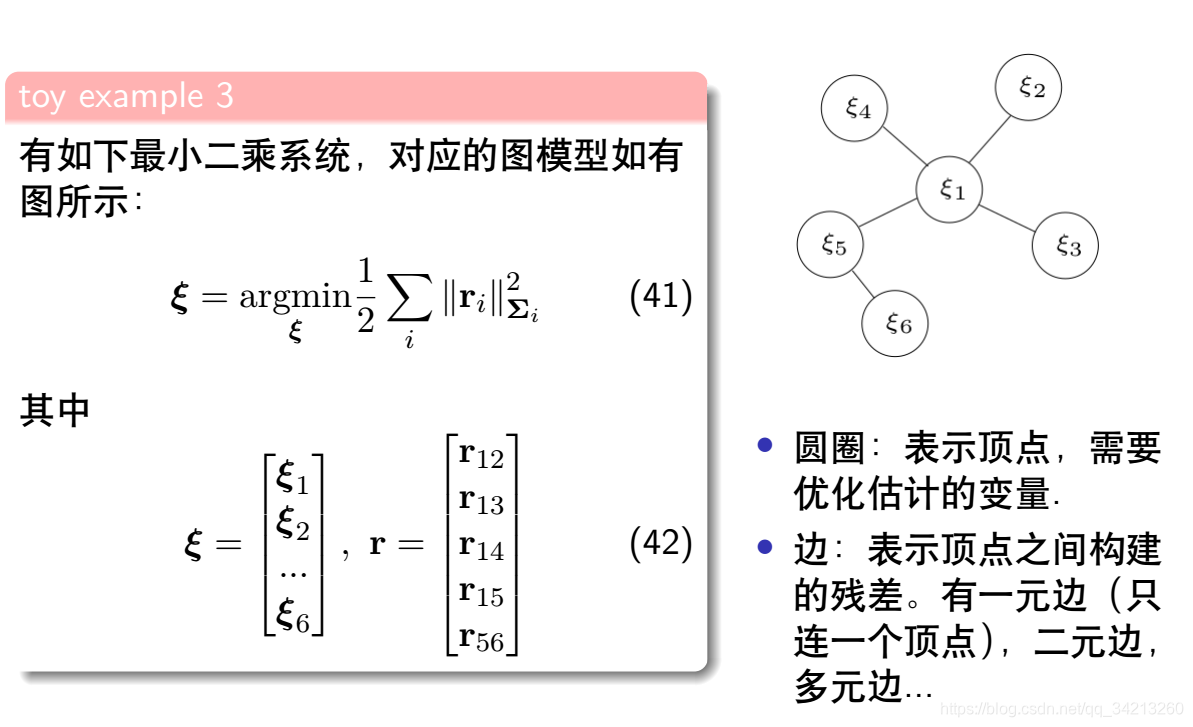
3.2 最小二乘问题信息矩阵的构成

3.3 信息矩阵的稀疏性

3.4 信息矩阵组装过程的可视化

3.5 基于边际概率的滑动窗口算法

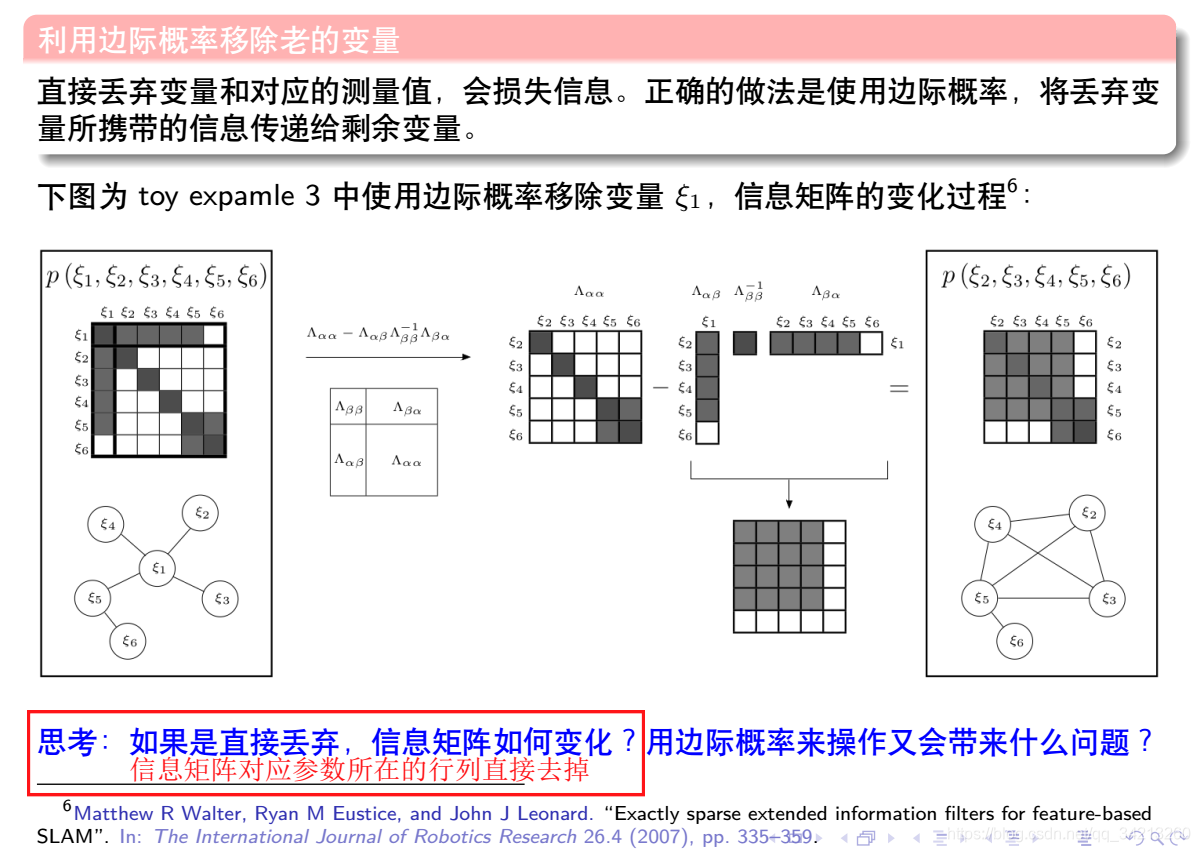
3.6 样例
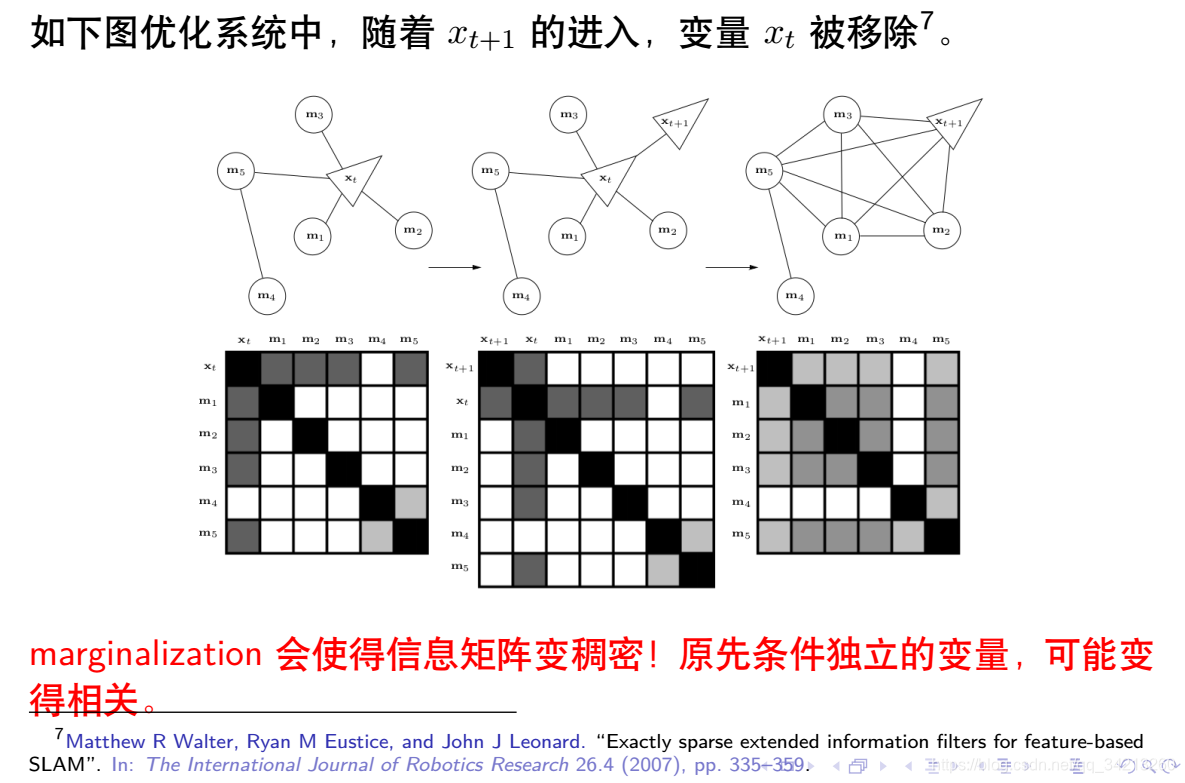
四、滑动窗口中的 FEJ 算法
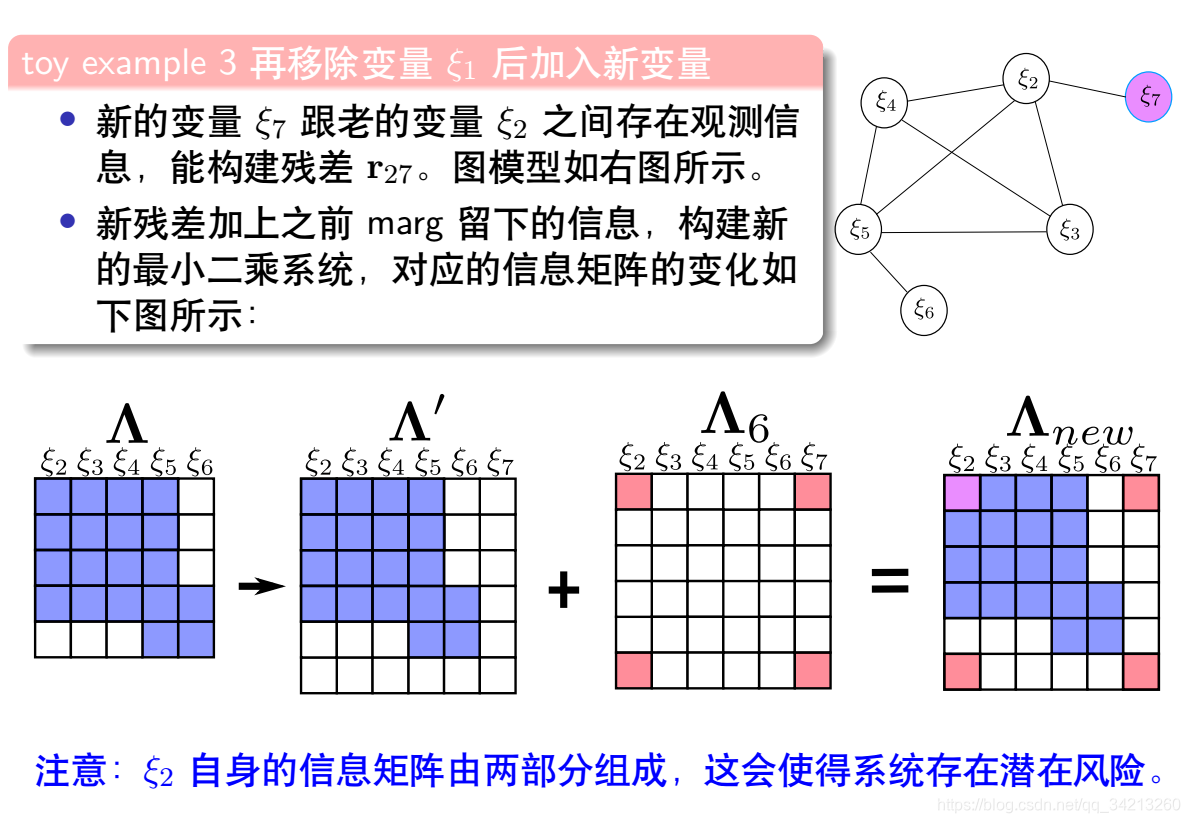


4.1 新测量信息和旧测量信息构建新的系统

4.2 信息矩阵的零空间变化


4.3 可观性的一种定义


