@
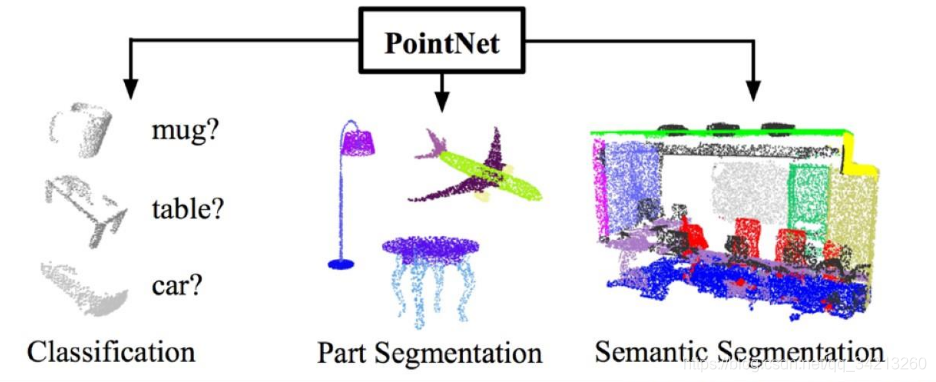
一、3D点云的挑战
- 以无序点云作为输入,因此模型需要具备
排序不变性 - 点云的旋转,平移不应该改变点云的类别,因此模型需要具备
几何变换不变性
二、排序不变性
排序不变性,即输入的点云的顺序不应该改变点云所代表的物体类别

当一个(N imes D) 在 N的维度上随意的打乱之后,其表述的应该是同一个物体。为了实现这一点。一个简单的方法是使用对称函数,如SUM和MAX等函数:
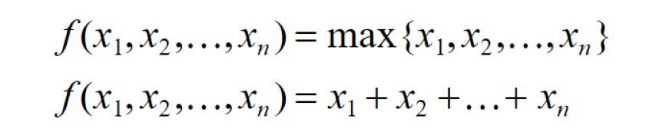
因此我们可以利用max函数设计一个很简单的点云网络,如下:
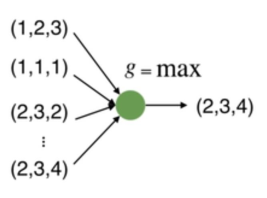
因此我们构造的网络也应是一个具有对称函数特特性的网络。但是这样的网络有一个问题,就是每个点损失的特征太多了,输出的全局特征仅仅继承了三个坐标轴上最大的那个特征,此时我们发现,当我们将点云的每个点先映射到一个冗余的高维空间后(例如1024维),再去进行max的对称函数操作,损失的特征就没那么多了。由此,就可以设计出这PointNet的雏形,称之为PointNet(vanilla):
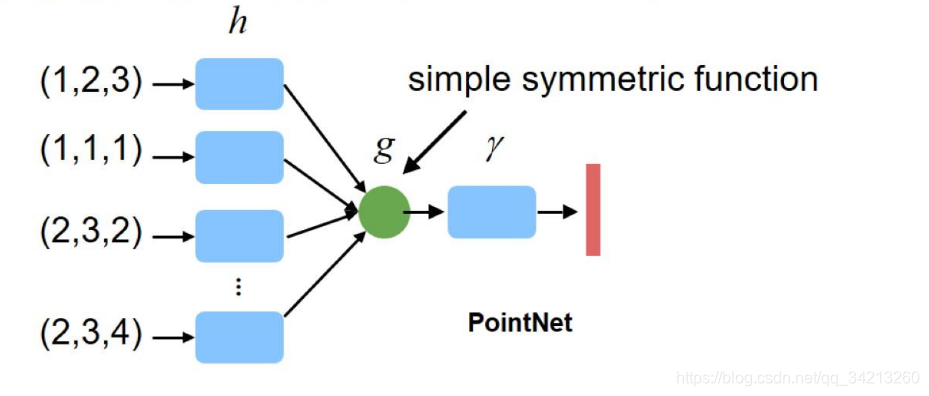
h:高维映射
g:对称函数
r:MLP
三、几何变换不变性
对于一个点云,进行平移和旋转之后应该表示的仍然是同一物体。
对于普通的PointNet(vanilla),如果先后输入同一个但是经过不同旋转角度的物体,它可能不能很好地将其识别出来。在论文中的方法是新引入了一个T-Net网络去学习点云的旋转,将物体校准,剩下来的PointNet(vanilla)只需要对校准后的物体进行分类或者分割即可。
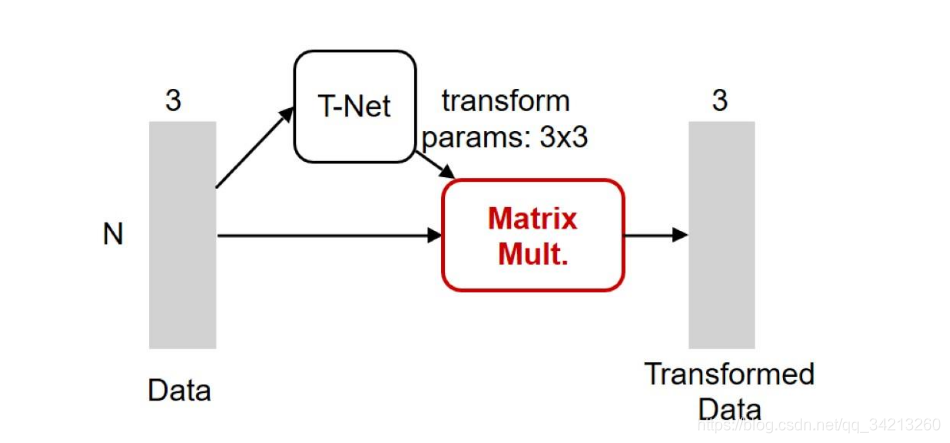
对于三维点的旋转只需乘以一个 3 × 3的旋转矩阵,即可将其矫正;同样的将点云映射到K维的冗余空间后,也是学习一个k×k的旋转矩阵,只不过因为旋转矩阵具有正交性,因此这次校对需要引入一个正则化惩罚项,希望其尽可能接近于一个正交矩阵。
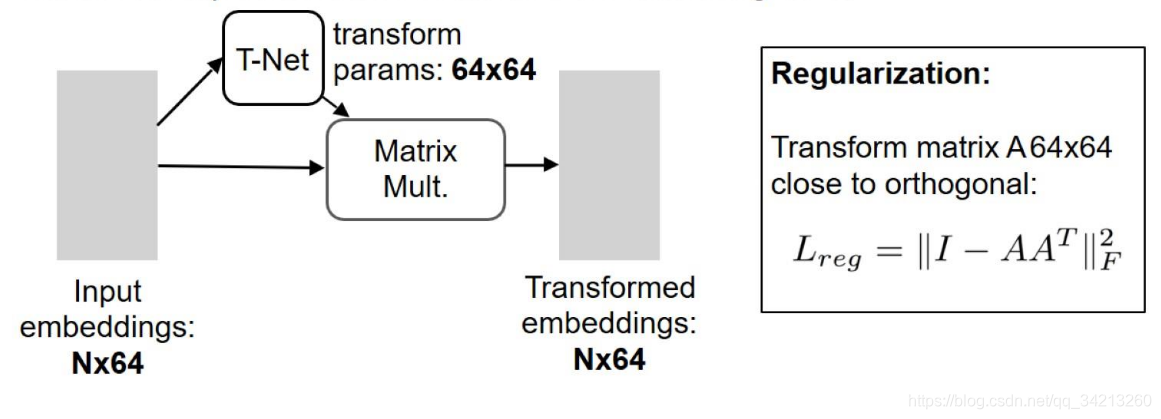
四、网络结构和代码实现
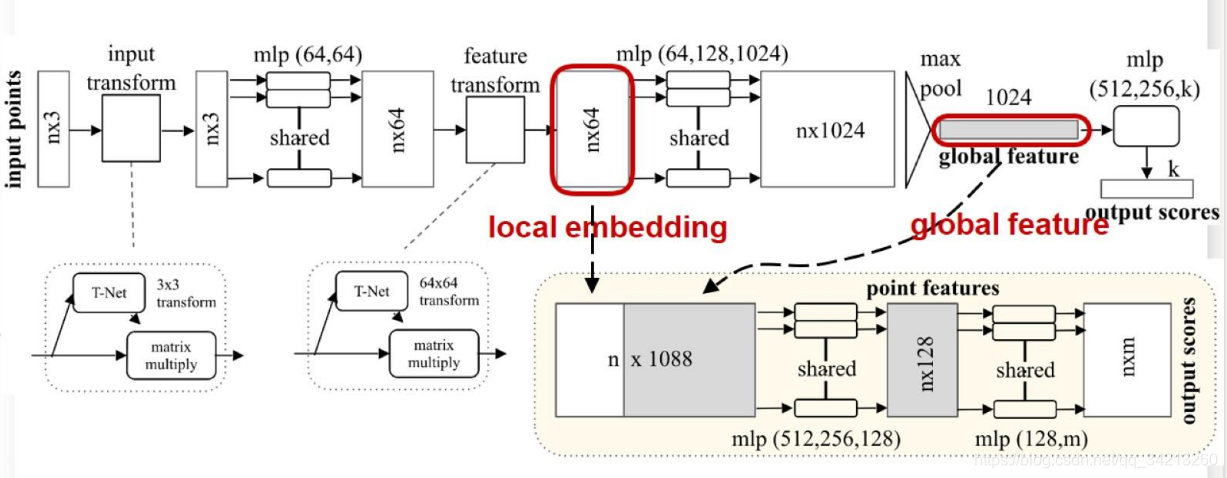
对于每一个 N × 3 的点云输入,网络先通过一个T-Net将其在空间上对齐(旋转到正面),再通过MLP将其映射到64维的空间上,再进行对齐,最后映射到1024维的空间上。这时对于每一个点,都有一个1024维的向量表征,而这样的向量表征对于一个3维的点云明显是冗余的,因此这个时候引入最大池化操作,将1024维所有通道上都只保留最大的那一个,这样得到的 1 × 1024的向量就是 N个点云的全局特征。
- 果做的是分类的问题,直接将这个全局特征再进过MLP去输出每一类的概率即可;
- 如果是分割问题,由于需要输出的是逐点的类别,因此其将全局特征拼接在了点云64维的逐点特征上,最后通过MLP,输出逐点的分类概率。