（环上）最大子段和

1.背景

最大连续子段和是一类问题，即求一个序列最大连续子序列的和。

问：给出n个元素分别为A1，A2，...，An，求出其最大连续子段和。

2.求解思路

2.1 动态规划：

设A[ i ]为该序列第 i 个元素，C[ i ]存放前 i 个序列的最大子段和，那么C[ i ]有两种可能结果：

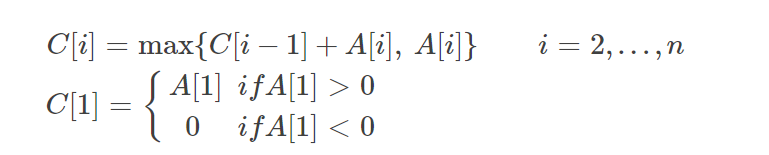
2.2 问题2：A1，A2，...，An 首尾相连，求出该环上最大子段和。

2.3 问题2解题思路：

• 如果子序列的最大和在 1 到 n 的范围内，直接输出最大和即可
• 如果子序列的最大和横跨了尾部和头部，则先求出连续的最小子序列和然后用总和减去最小子串和就是最大子串和

2.4 问题2代码示例：

#include<cstdio>
#include<algorithm> 
using namespace std;

const int maxn = 2e5+10;
const int INF = 0x3f3f3f3f;
int a[maxn];
typedef long long ll;
ll sum[maxn],minsum[maxn];
int main(){
	int n;
	ll s = 0;
	scanf("%d",&n);
	for(int i = 0;i < n;i++) scanf("%d",a+i),s += a[i];
	minsum[0] = sum[0] = a[0];
	for(int i = 1;i < n;i++){
		sum[i] = max(sum[i-1]+a[i],(ll)a[i]);
		minsum[i] = min(minsum[i-1]+a[i],(ll)a[i]);
	}
	ll mx = -INF,mi = INF;
	for(int i = 0;i < n;i++){
		mx = max(mx,sum[i]);
		mi = min(mi,minsum[i]);
	}
	ll ans = max(s-mi,mx);
	printf("%lld
",ans);
	return 0;
}