简介:Miller_Rabin法是一种简便的素数测试方法,一般用于测试大数是否为素数。
Miller_Rabin测试原理:如果n是素数,且与a互质,则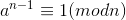
证明:请参考费马小定理证明方法。
思路:依据上述原理,我们可以不断选取与 n 互质的 a ,如果上式(1)都成立的话,那么n可能是一个素数,否则一定不是一个素数。如此一来只要a取得够多,就可以保证结果的准确度。一般在32位内的任一个整数n,如果其通过以2、7、61为底的Miller_Rabin测试,那其一定是素数,反之则一定不是。
优化:通过(1)式,只能说大概率验证素性,但是仅仅如此是不够的,为了减少误判的可能,同时大大减少计算量,可以通过如下结论进行优化:
定理:如果
,则必有
或
。
如果有一个大于2的质数 n ,令 n - 1 = 2^s * d,其中d为奇数,根据费马小定理,如果a不能被素数n整除,那么
。于是可以得出:,
或者
,
,(0<= r < s)。
于是只要找到一个a,满足
或者存在一个自然数r(0 <= r < s),使得
,就可以说明n一定不是素数,反之则有可能是素数。
模板:
#include<cstdio>
typedef long long ll;
ll qpow(ll a,ll b,ll m){ //快速幂算法
ll res = 1;
while(b){
if(b&1) res = res*a%m;
a = a*a%m;
b >>= 1;
}
return res%m;
}
bool Miller(ll x,ll n){ //Miller_Rabin测试
ll b = n-1;
while(!(b&1)) b >>= 1;
x = qpow(x,b,n); //此时b为没有因子2的奇数
while(b < n-1 && x != 1 && x != n-1)
x = (x*x)%n,b <<= 1;
return x == n-1 || b&1 == 1;
//当x=n-1,或b为奇数时返回true;
}
bool isPrime(ll n){
if(n == 2 || n == 7 || n == 61) return true;
if(n == 1 || !(n&1)) return false;
return Miller(2,n)&&Miller(7,n)&&Miller(61,n);
}
int main(){
ll n;
scanf("%lld",&n);
if(isPrime(n)) puts("Yes");
else puts("No");
}