前面介绍过的都是线性的数据结构,本文将介绍一种非线性数据结构——树,它对于存储需要快速查找的数据非常有用。树是一种一对多的数据结构,树这种数据结构在生活中经常看到,如 组织结构图
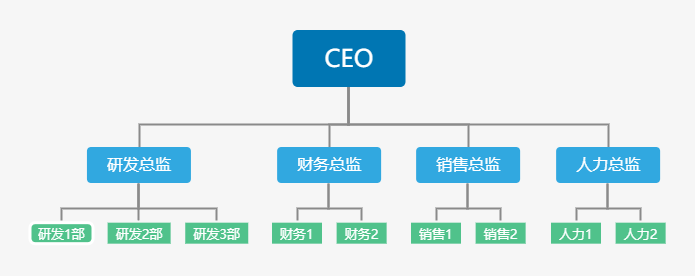
图中每个元素我们叫做节点,即树(Tree)可以理解为是n(n>=0)个节点的有限集合。当n=0时称为空树。
基本概念
树这种数据结构跟现实生活中的树很相似,树中的元素叫节点,其中连接相邻节点之间具有层级关系的叫做父子关系。
比如下面这幅图,A 节点就是 B 节点的父节点,B 节点是 A 节点的子节点。B、C、D 这三个节点的父节点是同一个节点,所以它们之间互称为兄弟节点。父节点为同一层的节点称为堂兄弟节点,也就是图中的B、C、D、K、L,及G、H、I、J。我们把没有父节点的节点叫做根节点,也就是图中的节点 E。我们把没有子节点的节点叫做叶子节点或者叶节点,比如图中的 G、H、I、J、K、L 都是叶子节点。

树还有三个比较相似的概念:高度(Height)、深度(Depth)、层(Level)。
节点的高度:节点到叶子节点的最长路径、边的个数
节点的深度:跟节点到这个节点的边的个数
节点的层数:节点的深度 + 1
树的高度:跟节点的高度
这三个概念的定义比较容易混淆,描述起来也比较空洞。我举个例子说明一下,你一看应该就能明白。
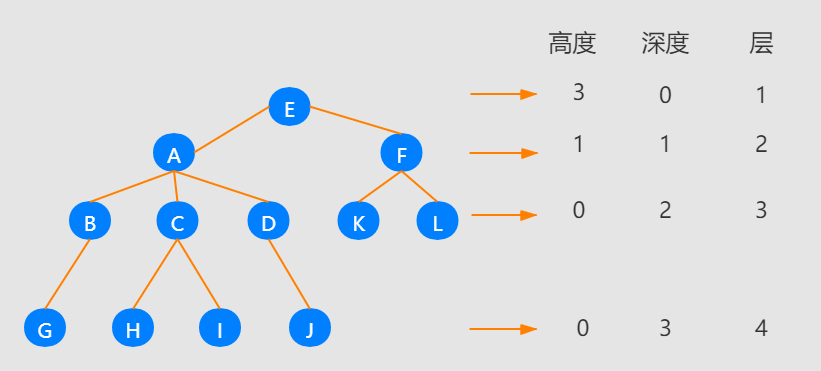
如图所示高度是从下往上递增,深度是上往下递增,层数是深度加 1。
二叉树
树结构多种多样,不过我们最常用还是二叉树。
二叉树,顾名思义,每个节点最多有两个叉,也就是两个子节点,分别是左子节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只有左子节点,有的节点只有右子节点。我画的这几个都是二叉树。

因为二叉树每个节点最多只有两个子节点,所以既可以用数组来存储,也可以用链表来存储。
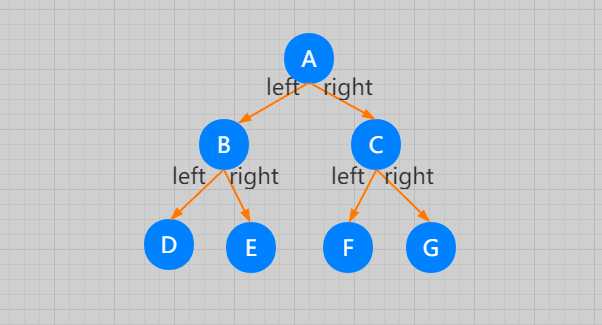
先来看比较简单、直观的链式存储法。从图中你应该可以很清楚地看到,每个节点有三个字段,其中一个存储数据,另外两个是指向左右子节点的指针。我们只要知道根节点,就可以通过左右子节点的指针,把整棵树都串起来,这种存储方式我们比较常用。大部分二叉树代码都是通过这种结构来实现的。
基于数组的顺序存储法。把根节点存储在下标 i = 1 的位置,那左子节点存储在下标 2 * i = 2 的位置,右子节点存储在 2 * i + 1 = 3 的位置。以此类推,B 节点的左子节点存储在 2 * i = 2 * 2 = 4 的位置,右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 5 的位置。
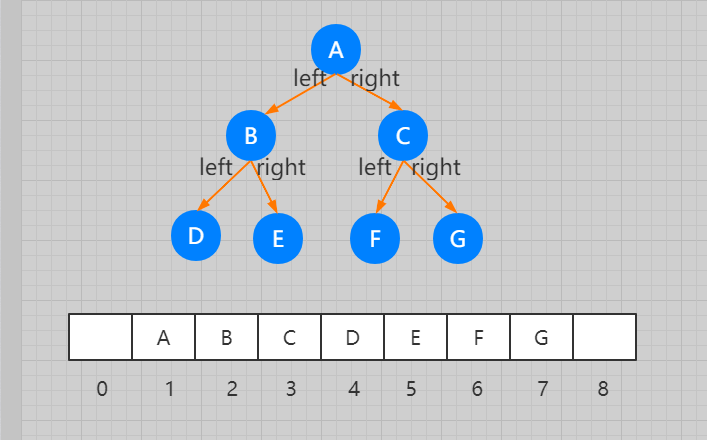
如图所示,如果节点 X 存储在数组中下标为 i 的位置,下标为 2 * i 的位置存储的就是左子节点,下标为 2 * i + 1 的位置存储的就是右子节点。反过来,下标为 i/2 的位置存储就是它的父节点。通过这种方式,我们只要知道根节点存储的位置(一般情况下,为了方便计算子节点,根节点会存储在下标为 1 的位置),这样就可以通过下标计算,把整棵树都串起来。
创建二叉树
观察上面的图我们可以知道,二叉树实际就是一个递归的过程,不断的左子树、右子树,直到该节点没有左子树或者右子树。递归需要一个临界点来结束递归,不然会死循环,从图中可以知道树终止递归其实就是没有左子树、右子树,也就是叶子节点,所以我们需要把叶子节点补上,用 # 来表示 如:
1 const arr = ['A','B','D','#','#','E','#','#','C','F','#', '#', 'G', '#', '#']
步骤:
- 先创建跟节点
- 递归创建左子树
- 递归创建右子树
先序遍历构建
1 /* 2 * @Description: 3 * @Version: 1.0 4 * @Autor: longbs 5 * 先序构建 6 */ 7 8 class Node { 9 constructor (data = '#') { 10 this.data = data 11 this.lNode = null 12 this.rNode = null 13 } 14 } 15 16 class BiTree { 17 root = null 18 nodeList = [] 19 constructor (nodeList) { 20 this.root = new Node() 21 this.nodeList = nodeList 22 } 23 createNode (node) { 24 const data = this.nodeList.shift() 25 if (data === '#') return 26 node.data = data 27 // 下一个元素是不是空节点, 如果不是创建左节点 28 if (this.nodeList[0] !== '#') { 29 node.lNode = new Node(data) 30 } 31 this.createNode(node.lNode) 32 33 // 下一个元素是不是空节点, 如果不是创建右节点 34 if (this.nodeList[0] !== '#') { 35 node.rNode = new Node(data) 36 } 37 this.createNode(node.rNode) 38 39 } 40 } 41 42 const arr = ['A','B','D','#','#','E','#','#','C','F','#', '#', 'G', '#', '#'] 43 const bi = new BiTree(arr) 44 bi.createNode(bi.root) 45 console.log(bi.root)
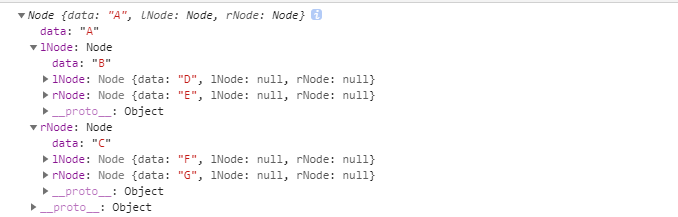
层级遍历构建
还可以一层一层的来构建,如先创建跟节点,在创建下一层的左子树、右子树,在继续创建左子树的下一层(左右子树)。
步骤:
- 先创建跟节点
- 创建左子树
- 创建右子树
- 重复2、3过程
通常这种层次的问题可以使用队列来解决,先将跟节点入队,把队列中的队首出队,将这个出队相关的节点入队,这样循环,一直到队列为空。
1 /* 2 * @Description: 3 * @Version: 1.0 4 * @Autor: longbs 5 * 层次构建 6 */ 7 class Node { 8 constructor (data = '#') { 9 this.data = data 10 this.lNode = null 11 this.rNode = null 12 } 13 } 14 15 class BiTreeByLevel { 16 root = null 17 constructor () { 18 this.root = null 19 } 20 createNode (nodeList) { 21 let queue = [] 22 if (!this.root) { 23 let nodeValue = nodeList.shift() 24 this.root = new Node(nodeValue) 25 queue.push(this.root) 26 } 27 while (queue.length) { 28 // 将队列队首出队,这个是树的跟节点或者子树的跟节点 29 let head= queue.shift() 30 // 找到相关的在入队 31 let nodeValue = nodeList.shift() 32 // 构建左节点 33 if (nodeValue !== '#') { 34 head.lNode = new Node(nodeValue) 35 queue.push(head.lNode) 36 } 37 // 右节点 38 nodeValue = nodeList.shift() 39 if (nodeValue !== '#') { 40 head.rNode = new Node(nodeValue) 41 queue.push(head.rNode) 42 } 43 } 44 } 45 } 46 47 let arr = ['A','B','C','D','E','F','G','#','#','#','#','#','#','#','#'] 48 let bi = new BiTreeByLevel(arr) 49 bi.createNode(arr) 50 console.log(bi.root)
今天先到这里吧,后面把二叉树先序、中序、后序、层次遍历,查找二叉树、红黑树补上。