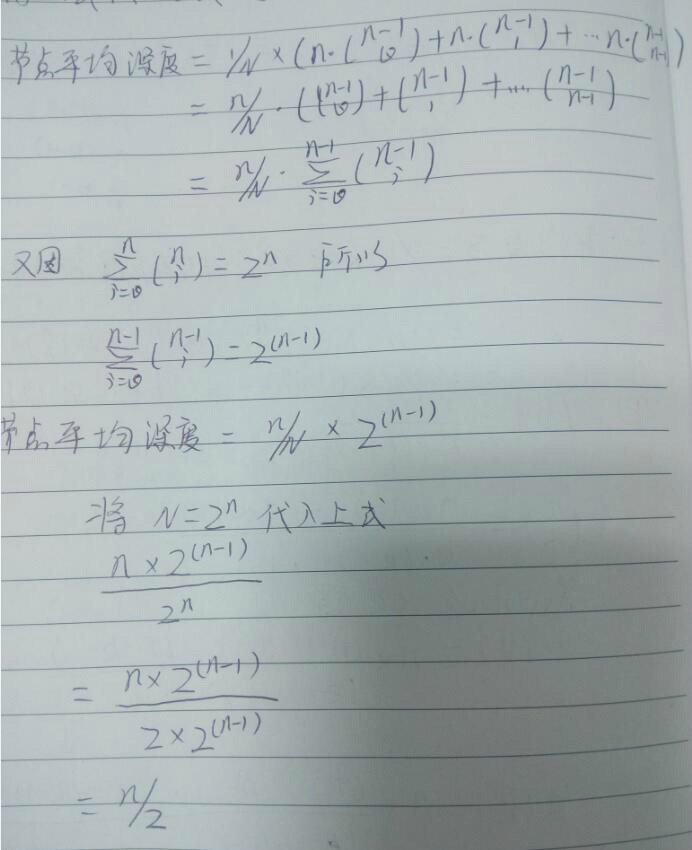1.5.15二项树。请证明,对于加权quick-union算法,在最坏情况下树中每一层的节点数均为二项式系数。在这种情况下,计算含有N=2^n个节点的树中节点的平均深度。
答:
1)最坏情况是指在指定的节点数目下构建最大深度的树,要构建最大深度的树就需要在树的每次合并都会使合并后的树高度增加,要使两棵树合并时树高增加,那么两个树的节点数应相同,那么构建树的次序为:
设节点总数为N。
1.1)把所有单节点两两合并成一棵树,形成N/2棵树。
1.2)再把所有两个节点树合并成一棵树,形成N/4棵树。
1.3)把把所有4节点树合并成一棵树,形成N/8棵树,以此继续直到所有节点形成一棵树。
生成树的过程如下图所示:
从树根到叶节点,每层的节点数为:1,3,3,1。二项式系数C(3,0),C(3,1),C(3,2),C(3,3) 的值为:1,3,3,1。(此处并不是数学证明)。
2)在树每层的节点数是二项式系数时节点的平均深度为n/2
2.1)树节点数为N=2^n时,树深度为:n
2.2)平均深度=所在层的深度X各层节点数 之和/所有节点数=n/2