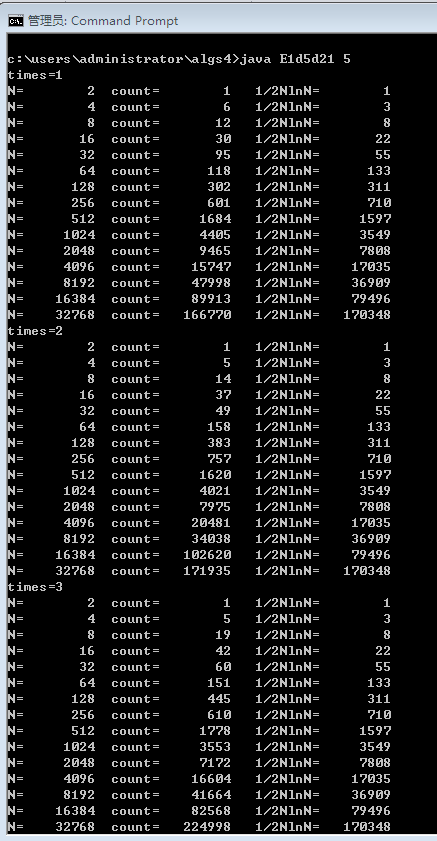
1.5.21Erdos-renyi模型。使用练习1.5.17的用例验证这个猜想:得到单个连通分量所需生成的整数对数量为~1/2NlnN。
public class E1d5d21
{
public static void main(String[] args)
{
int T=Integer.parseInt(args[0]);
for (int t=1;t<=T;t++)
{
StdOut.println("times=" + t);
for (int i=2;i<Math.pow(2,16);i=2*i)
StdOut.printf("N=%9d count=%9d 1/2NlnN=%9.0f ",i, ErdosRenyi.count(i),0.5*i*Math.log(i));
}
}
}

public class E1d5d21
{
public static void main(String[] args)
{
int T=Integer.parseInt(args[0]);
for (int t=1;t<=T;t++)
{
StdOut.println("times=" + t);
for (int i=2;i<Math.pow(2,16);i=2*i)
StdOut.printf("N=%9d count=%9d 1/2NlnN=%9.0f ",i, ErdosRenyi.count(i),0.5*i*Math.log(i));
}
}
}