Algs4-2.4.3用无/有序数组、无/有序链表实现优先队列（大堆）

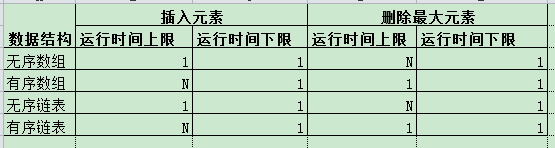
2.4.3用以下数据结构实现优先队列，支持插入元素和删除最大元素的操作：无序数组、有序数组、无序链表和链表。将你的4种实现中的每种操作在最坏情况下的运行时间上下限制成一张表格。

1)无序数组实现优先队列大堆
public class E2d4d3v1<Key extends Comparable<Key>>
{
    //无序数组实现优先队列大堆
    private Key[] pq;
    private int N=0;
   
    public  E2d4d3v1(int maxN)
    { pq=(Key[]) new Comparable[maxN];}
   
    public boolean isEmpty()
    { return N==0;}
   
    public int size()
    { return N;}
   
    public void Insert(Key v)
    {
        pq[N++]=v;
      }
    public Key delMax()
    {
        int maxIndex=0;
        for (int i=0;i<N;i++)
           if(less(maxIndex,i))
              maxIndex=i;
        Key max=pq[maxIndex];
        N--;
        exch(maxIndex,N);
        pq[N]=null;
       
        return max;
    }

    private boolean less(int i,int j)
    { return pq[i].compareTo(pq[j])<0;}
   
    private void exch(int i,int j)
    {
        Key tmp=pq[i];
        pq[i]=pq[j];
        pq[j]=tmp;
    }
   
    public static void main(String[] args)
    {
        E2d4d3v1 pq=new E2d4d3v1(3);
        pq.Insert(1);
        pq.Insert(3);
        StdOut.println(pq.delMax());
        pq.Insert(2);
        StdOut.println(pq.delMax());
        StdOut.println(pq.delMax());
    }
}


2)有序数组实现优先队列大堆,pq[n]存储最小元素

public class E2d4d3v2<Key extends Comparable<Key>>
{
    //有序数组实现优先队列大堆
    //pq[0]存储最小元素
    private Key[] pq;
    private int N=0;
   
    public  E2d4d3v2(int maxN)
    { pq=(Key[]) new Comparable[maxN];}
   
    public boolean isEmpty()
    { return N==0;}
   
    public int size()
    { return N;}
   
    public void Insert(Key v)
    {
       int i;
       for(i=N-1;i>=0 && less(v,pq[i]);i--)
           pq[i+1]=pq[i];
       pq[i+1]=v;
       N++;
      }
    public Key delMax()
    {
        Key max=pq[--N];
        pq[N]=null;
       
        return max;
    }

    private boolean less(Key v,Key w)
    { return v.compareTo(w)<0;}
   
    private void exch(int i,int j)
    {
        Key tmp=pq[i];
        pq[i]=pq[j];
        pq[j]=tmp;
    }
   
    public static void main(String[] args)
    {
       E2d4d3v2 pq=new E2d4d3v2(3);
        pq.Insert(1);
        pq.Insert(3);
        StdOut.println(pq.delMax());
        pq.Insert(2);
        StdOut.println(pq.delMax());
        StdOut.println(pq.delMax());
 
    }
}

3)无序链表实现优先队列大堆
public class E2d4d3v3<Key extends Comparable<Key>>
{
    private class Node
    {
        Key item;
        Node next;
    }
    //无序链表实现优先队列大堆
    private Node first;
    private int N=0;
   
    
    public boolean isEmpty()
    { return N==0;}
   
    public int size()
    { return N;}
   
    public void Insert(Key v)
    {
       Node Item=new Node();
       Item.item=v;
       Item.next=first;
       first=Item;
       N++;
      }
   
    public Key delMax()
    {
        Node Item=new Node();
        Item.next=first;
       
        Node maxItem=first;
        Node maxItemPrev=Item;

        while(Item.next.next!=null)
        {
          if(less(maxItem.item,Item.next.next.item))
          {
              maxItem=Item.next.next;
              maxItemPrev=Item.next;
          }
          Item=Item.next;
        }
       
        Key max=maxItem.item;
        maxItemPrev.next=maxItem.next;
        if(first==maxItem) first=maxItem.next;
        maxItem=null;
        N--;
        return max;
    }

    private boolean less(Key v,Key w)
    { return v.compareTo(w)<0;}
   
    public static void main(String[] args)
    {
        E2d4d3v3 pq=new E2d4d3v3();
        pq.Insert(1);
        pq.Insert(3);
        StdOut.println(pq.delMax());
        pq.Insert(2);
        StdOut.println(pq.delMax());
        StdOut.println(pq.delMax());
    }
}

4)有序链表实现优先队列大堆,first存储最大元素

public class E2d4d3v4<Key extends Comparable<Key>>
{
    private class Node
    {
        Key item;
        Node next;
    }
    //有序链表实现优先队列大堆,first存储最大元素
    private Node first;
    private int N=0;
   
    
    public boolean isEmpty()
    { return N==0;}
   
    public int size()
    { return N;}
   
    public void Insert(Key v)
    {
       Node newItem=new Node();
       newItem.item=v;
      
       Node Item=new Node();
       Item.next=first;
         
        while(Item.next!=null && less(newItem.item,Item.next.item))
             Item=Item.next;
      
        newItem.next=Item.next;
        Item.next=newItem;
        //0节点增加新节点 或 新节点为最大时修改first
        if(first==null || first==newItem.next)   first=newItem;
        N++;
      }
   
    public Key delMax()
    {
       Node maxItem=first;
       first=first.next;
       Key max=maxItem.item;
       N--;
        return max;
    }

    private boolean less(Key v,Key w)
    { return v.compareTo(w)<0;}
   
    public static void main(String[] args)
    {
        E2d4d3v4 pq=new E2d4d3v4();
        pq.Insert(1);
        pq.Insert(3);
        StdOut.println(pq.delMax());
        pq.Insert(2);
        StdOut.println(pq.delMax());
        StdOut.println(pq.delMax());
    }
}