问题描述
给定一个n*n的棋盘,棋盘中有一些位置不能放皇后。现在要向棋盘中放入n个黑皇后和n个白皇后,使任意的两个黑皇后都不在同一行、同一列或同一条对角线上,任意的两个白皇后都不在同一行、同一列或同一条对角线上。问总共有多少种放法?n小于等于8。
输入格式
输入的第一行为一个整数n,表示棋盘的大小。
接下来n行,每行n个0或1的整数,如果一个整数为1,表示对应的位置可以放皇后,如果一个整数为0,表示对应的位置不可以放皇后。
接下来n行,每行n个0或1的整数,如果一个整数为1,表示对应的位置可以放皇后,如果一个整数为0,表示对应的位置不可以放皇后。
输出格式
输出一个整数,表示总共有多少种放法。
样例输入
4
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
样例输出
2
蓝桥杯的话,最难的和出现最多的应该就是dfs,bfs和动态规划了,这也是一道典型的dfs,基本思路是穷尽尝试,如果某次尝试失败,则退回上一步重新选择。
接下来对这一题作具体分析:
1.要找出所有可能,每种可能要求同行,同列,同对角线上不能出现同种颜色皇后,首先想到的应该是先放一种颜色的皇后,再放另一种。
那么先放黑皇后,再放白皇后,每种皇后都从第一行遍历到最后一行,每行再逐列尝试。
2.在每次放皇后时,需要判断同行,同列,同对角线上是否已经出现了同种颜色的皇后,所以每次放过皇后后要标记这三个值。接下来讲如何标记这三个值:
3.因为是从第一行遍历到最后一行,所以不需要考虑行,而列只需要设置一个数组,每次放入一个皇后,在相应的vis数组标记为1。
至于同对角线,有两种情况,从左下到右上的对角线,我暂且称之为斜1;从左上到右下,记作斜2;
(1)很容易可以看出在斜1同一条对角线上的横纵坐标相加是一个固定的数,且每条对角线不会重复,0,2,4,6.....所以直接把这个相加之后固定的数作为数组的下标,每次放入之后标记为1;
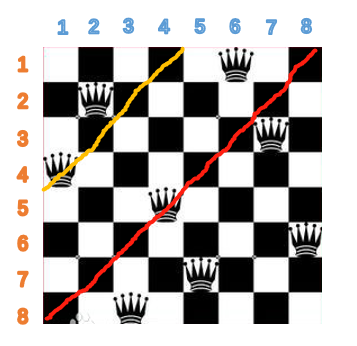
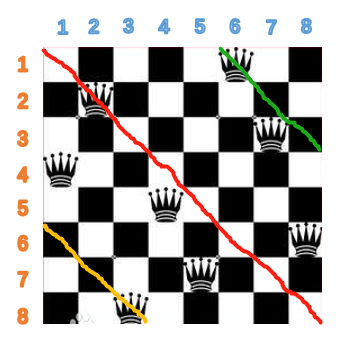
(2)同理,斜2同一条对角线上横纵坐标相减为一个固定的数,为了防止出现负数,统一加7
(具体见18,19行和42,43行)
到这里这道题的难点就结束了,代码中有更详细的注释
1 #include<iostream> 2 using namespace std; 3 int n ,ans = 0; 4 int qp[8][8];//棋盘 5 // 0不能放;1能放;2黑皇后;3白皇后 6 int lieblack[8]{ 0 }, liewhite[8]{ 0 };// 0/1标记该列是否被黑/白皇后占用 7 int xie1black[20]{ 0 }, xie2black[20]{ 0 }, xie1white[20]{ 0 }, xie2white[20]{ 0 }; 8 //标记左斜行和右斜行 9 void dfswhite(int hang) //参数为当前的行数 10 { 11 if (hang == n) //当白皇后最后一行也已经放完之后 12 { 13 ans++; //已经是一种成功放置的方法 14 return ; 15 } 16 for (int lie = 0; lie < n; lie++) //在每行中遍历 17 { 18 if (qp[hang][lie] == 1 && liewhite[lie] == 0 && xie1white[hang + lie] == 0 19 && xie2white[hang - lie + 7] == 0)//判断条件依次为,棋盘是否能放;该列是否被同颜色皇后占用; 20 //斜1对角线是否被占用;斜2对角线是否被占用; 21 { 22 qp[hang][lie] = 2; //放置皇后,依次标记 23 liewhite[lie] = 1; 24 xie1white[hang + lie] = 1; 25 xie2white[hang - lie + 7] = 1; 26 dfswhite(hang + 1); //该行已放置,进入下一行 27 qp[hang][lie] = 1; //回溯,移除标记 28 liewhite[lie] = 0; 29 xie1white[hang + lie] = 0; 30 xie2white[hang - lie + 7] = 0; 31 } 32 } 33 } 34 void dfsblack(int hang) 35 { 36 if (hang == n) //当黑皇后最后一行也已经放置 37 { 38 dfswhite(0);//开始放置白皇后 39 return ; 40 } 41 for (int lie = 0; lie < n; lie++) //与dfswhite同理 42 { 43 if (qp[hang][lie] == 1 && lieblack[lie] == 0 && xie1black[hang + lie] == 0 44 && xie2black[hang - lie + 7] == 0) 45 { 46 qp[hang][lie] = 3; 47 lieblack[lie] = 1; 48 xie1black[hang + lie] = 1; 49 xie2black[hang - lie + 7] = 1; 50 dfsblack(hang + 1); 51 qp[hang][lie] = 1; 52 lieblack[lie] = 0; 53 xie1black[hang + lie] = 0; 54 xie2black[hang - lie + 7] = 0; 55 } 56 } 57 } 58 int main() 59 { 60 cin >> n; 61 for (int i = 0; i < n; i++) 62 { 63 for (int j = 0; j < n; j++) 64 { 65 cin >> qp[i][j]; 66 } 67 } 68 dfsblack(0);//从第一行开始防止黑皇后,全部放置完后再放置白皇后 69 cout << ans; 70 }