leetcode刷题需要经常用的二叉树,发现二叉树这种可以无限扩展知识点来虐别人的数据结构,很受面试官的青睐,这里记录一下Java定义二叉树和遍历。
一、什么是二叉树
1 .二叉树的性质
本身是有序树,树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2
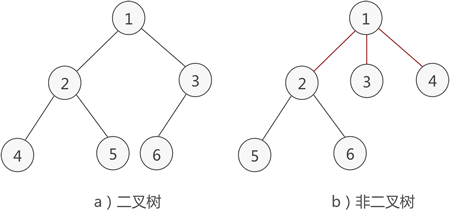
图 1 二叉树示意图
二叉树具有以下几个性质:
- 二叉树中,第 i 层最多有 2i-1 个结点。
- 如果二叉树的深度为 K,那么此二叉树最多有 2K-1 个结点。
- 二叉树中,终端结点数(叶子结点数)为 n0,度为 2 的结点数为 n2,则 n0=n2+1。
性质 3 的计算方法为:对于一个二叉树来说,除了度为 0 的叶子结点和度为 2 的结点,剩下的就是度为 1 的结点(设为 n1),那么总结点 n=n0+n1+n2。
同时,对于每一个结点来说都是由其父结点分支表示的,假设树中分枝数为 B,那么总结点数 n=B+1。而分枝数是可以通过 n1 和 n2 表示的,即 B=n1+2*n2。所以,n 用另外一种方式表示为 n=n1+2*n2+1。
两种方式得到的 n 值组成一个方程组,就可以得出 n0=n2+1。
2 .满二叉树
如果二叉树中除了叶子结点,每个结点的度都为 2,则此二叉树称为满二叉树
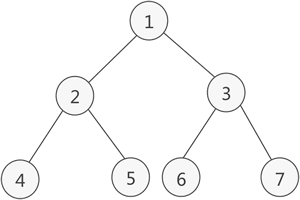
图 2 满二叉树示意图
满二叉树除了满足普通二叉树的性质,还具有以下性质:
- 满二叉树中第 i 层的节点数为 2n-1 个。
- 深度为 k 的满二叉树必有 2k-1 个节点 ,叶子数为 2k-1。
- 满二叉树中不存在度为 1 的节点,每一个分支点中都两棵深度相同的子树,且叶子节点都在最底层。
- 具有 n 个节点的满二叉树的深度为 log2(n+1)。
3 .完全二叉树
如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树
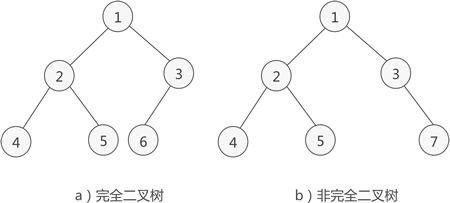
图 3 完全二叉树示意图
如图 3a) 所示是一棵完全二叉树,图 3b) 由于最后一层的节点没有按照从左向右分布,因此只能算作是普通的二叉树。
完全二叉树除了具有普通二叉树的性质,它自身也具有一些独特的性质,比如说,n 个结点的完全二叉树的深度为 ⌊log2n⌋+1。
⌊log2n⌋ 表示取小于 log2n 的最大整数。例如,⌊log24⌋ = 2,而 ⌊log25⌋ 结果也是 2。
对于任意一个完全二叉树来说,如果将含有的结点按照层次从左到右依次标号(如图 3a)),对于任意一个结点 i ,完全二叉树还有以下几个结论成立:
- 当 i>1 时,父亲结点为结点 [i/2] 。(i=1 时,表示的是根结点,无父亲结点)
- 如果 2*i>n(总结点的个数) ,则结点 i 肯定没有左孩子(为叶子结点);否则其左孩子是结点 2*i 。
- 如果 2*i+1>n ,则结点 i 肯定没有右孩子;否则右孩子是结点 2*i+1 。
二、二叉树的存储结构
二叉树的存储结构有两种,分别为顺序存储和链式存储。
1 .顺序存储
二叉树的顺序存储,指的是使用顺序表(数组)存储二叉树。需要注意的是,顺序存储只适用于完全二叉树。换句话说,只有完全二叉树才可以使用顺序表存储。因此,如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树。满二叉树也可以使用顺序存储。要知道,满二叉树也是完全二叉树,因为它满足完全二叉树的所有特征。
普通二叉树转完全二叉树的方法很简单,只需给二叉树额外添加一些节点,将其"拼凑"成完全二叉树即可。如图 1 所示:
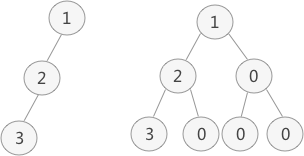
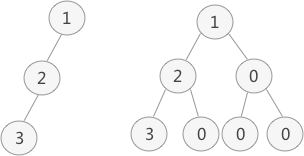
图 1 普通二叉树的转化
图 1 中,左侧是普通二叉树,右侧是转化后的完全(满)二叉树。
解决了二叉树的转化问题,接下来学习如何顺序存储完全(满)二叉树。
完全二叉树的顺序存储,仅需从根节点开始,按照层次依次将树中节点存储到数组即可。

图 2 完全二叉树示意图
例如,存储图 2 所示的完全二叉树,其存储状态如图 3 所示:


图 3 完全二叉树存储状态示意图
同样,存储由普通二叉树转化来的完全二叉树也是如此。例如,图 1 中普通二叉树的数组存储状态如图 4 所示:


图 4 普通二叉树的存储状态
由此,我们就实现了完全二叉树的顺序存储。
不仅如此,从顺序表中还原完全二叉树也很简单。我们知道,完全二叉树具有这样的性质,将树中节点按照层次并从左到右依次标号(1,2,3,...),若节点 i 有左右孩子,则其左孩子节点为 2*i,右孩子节点为 2*i+1。此性质可用于还原数组中存储的完全二叉树,也就是实现由图 3 到图 2、由图 4 到图 1 的转变。
2 .链式存储
其实二叉树并不适合用数组存储,因为并不是每个二叉树都是完全二叉树,普通二叉树使用顺序表存储或多或多会存在空间浪费的现象。
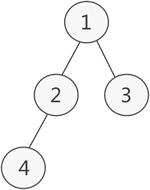
图 1 普通二叉树示意图
如图 1 所示,此为一棵普通的二叉树,若将其采用链式存储,则只需从树的根节点开始,将各个节点及其左右孩子使用链表存储即可。因此,图 1 对应的链式存储结构如图 2 所示:
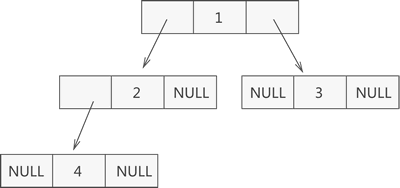
图 2 二叉树链式存储结构示意图
由图 2 可知,采用链式存储二叉树时,其节点结构由 3 部分构成(如图 3 所示):
- 指向左孩子节点的指针(Lchild);
- 节点存储的数据(data);
- 指向右孩子节点的指针(Rchild);

图 3 二叉树节点结构
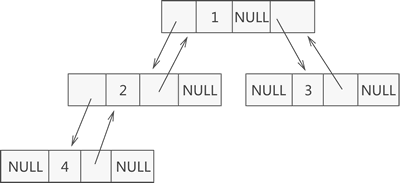
图 4 自定义二叉树的链式存储结构
这样的链表结构,通常称为三叉链表。
利用图 4 所示的三叉链表,我们可以很轻松地找到各节点的父节点。因此,在解决实际问题时,用合适的链表结构存储二叉树,可以起到事半功倍的效果。
三、java实现二叉树
1.Node节点的定义
我们需要自定义一个Node类
package com.hanwl.leetcode; /** * @Author hanwl * @Date 2021-03-26 10:30 * @Version 1.0 * 定义二叉树的一个节点node */ public class Node { private int value; //节点的值 private Node node; //此节点,数据类型为Node private Node left; //此节点的左子节点,数据类型为Node private Node right; //此节点的右子节点,数据类型为Node public Node() { } public Node(int value) { this.value = value; this.left = null; this.right = null; } public int getValue() { return value; } public void setValue(int value) { this.value = value; } public Node getNode() { return node; } public void setNode(Node node) { this.node = node; } public Node getLeft() { return left; } public void setLeft(Node left) { this.left = left; } public Node getRight() { return right; } public void setRight(Node right) { this.right = right; } }
2.数组转换二叉树
数组存储方式和树的存储方式可以相互转换,即数组可以转换成树,树也可以转换成数组
顺序二叉树通常只考虑完全二叉树
第n个元素的左子节点为 2 * n + 1
第n个元素的右子节点为 2 * n + 2
第n个元素的父节点为 (n-1) / 2
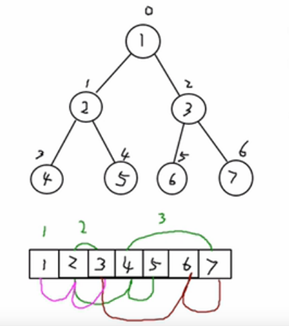
n : 表示二叉树中的第几个元素(按0开始编号,如图所示)
对于具有n个节点的完全二叉树,如果按照从上至下和从左至右的顺序对所有节点序号从0开始顺序编号,则对于序号为i(0<=i< n)的节点有:
如果i>0,则序号为i节点的双亲节点的序号为(i-1)/2(/为整除);如果i=0,则序号为i节点为根节点,无双亲节点 如果2i+1<n,则序号为i节点的左孩子节点的序号为2i+1;
如果2i+1>=n,则序号为i节点无左孩子 如果2i+2<n,则序号为i节点的右孩子节点的序号为2i+2;如果2i+2>=n,则序号为i节点无右孩子
package com.hanwl.leetcode; import java.util.ArrayDeque; import java.util.ArrayList; import java.util.List; import java.util.Stack; /** * @Author hanwl * @Date 2021-03-26 10:36 * @Version 1.0 一般拿到的数据是一个int型的数组,那怎么将这个数组变成我们可以直接操作的树结构呢? 1、数组元素变Node类型节点 2、给N/2-1个节点设置子节点 3、给最后一个节点设置子节点【有可能只有左节点】 */ public class TreeNode { public static void main(String[] args) { int[] array = {1, 2, 3, 4, 5, 6, 7}; List<Node> list = new ArrayList<>(); TreeNode treeNode = new TreeNode(); treeNode.create(array,list); // nodeList中第0个索引处的值即为根节点 Node root = list.get(0); System.out.println("先序遍历:"); preOrderTraverse(root); System.out.println(); System.out.println("中序遍历:"); inOrderTraverse(root); System.out.println(); System.out.println("后序遍历:"); postOrderTraverse(root); System.out.println(); System.out.println("非递归先序遍历:"); preOrderTraversalbyLoop(root); System.out.println(); System.out.println("非递归中序遍历:"); inOrderTraversalbyLoop(root); System.out.println(); System.out.println("非递归后序遍历:"); postOrderTraversalbyLoop(root); System.out.println(); System.out.println("广度优先遍历:"); levelOrderTraversal(root); System.out.println(); System.out.println("深度优先遍历:"); depthTraversal(root); } //创建二叉树 public void create(int[] datas, List<Node> list){ // 将数组里面的东西变成节点的形式 for(int i=0;i<datas.length;i++) { Node node=new Node(datas[i]); list.add(node); } // 节点关联成树 for(int index=0;index<list.size()/2-1;index++){ //编号为n的节点他的左子节点编号为2*n 右子节点编号为2*n+1 但是因为list从0开始编号,所以还要+1 list.get(index).setLeft(list.get(index*2+1)); //与上同理 list.get(index).setRight(list.get(index*2+2)); } // 最后一个父节点,因为最后一个父节点可能没有右孩子,所以单独拿出来处理 避免单孩子情况 int lastParentIndex=list.size()/2-1; list.get(lastParentIndex).setLeft(list.get(lastParentIndex*2+1)); if (list.size()%2==1) { // 如果有奇数个节点,最后一个父节点才有右子节点 list.get(lastParentIndex).setRight(list.get(lastParentIndex*2+2)); } } /** * 先序遍历 * * 这三种不同的遍历结构都是一样的,只是先后顺序不一样而已 * * @param node * 遍历的节点 */ public static void preOrderTraverse(Node node) { if (node == null) return; System.out.print(node.getValue() + " "); preOrderTraverse(node.getLeft()); preOrderTraverse(node.getRight()); } /** * 中序遍历 * * 这三种不同的遍历结构都是一样的,只是先后顺序不一样而已 * * @param node * 遍历的节点 */ public static void inOrderTraverse(Node node) { if (node == null) return; inOrderTraverse(node.getLeft()); System.out.print(node.getValue() + " "); inOrderTraverse(node.getRight()); } /** * 后序遍历 * * 这三种不同的遍历结构都是一样的,只是先后顺序不一样而已 * * @param node * 遍历的节点 */ public static void postOrderTraverse(Node node) { if (node == null) return; postOrderTraverse(node.getLeft()); postOrderTraverse(node.getRight()); System.out.print(node.getValue() + " "); } /** * 非递归前序遍历 * 基本的原理就是当循环中的p不为空时,就读取p的值,并不断更新p为其左子节点,即不断读取左子节点, * 直到一个枝节到达最后的子节点,再继续返回上一层进行取值 * * 我这里使用了栈这个数据结构,用来保存不到遍历过但是没有遍历完全的父节点,之后再进行回滚。 * */ public static void preOrderTraversalbyLoop(Node node){ Stack<Node> stack = new Stack(); Node p = node; while(p!=null || !stack.isEmpty()){ while(p!=null){ //当p不为空时,就读取p的值,并不断更新p为其左子节点,即不断读取左子节点 System.out.print(p.getValue()+" "); stack.push(p); //将p入栈 p = p.getLeft(); } if(!stack.isEmpty()){ p = stack.pop(); p = p.getRight(); } } } /** *非递归中序遍历 * 基本原理就是当循环中的p不为空时,就读取p的值,并不断更新p为其左子节点,但是切记这个时候不能进行输出,必须不断读取左子节点, * 直到一个枝节到达最后的子节点,然后每次从栈中拿出一个元素,就进行输出,再继续返回上一层进行取值 * */ public static void inOrderTraversalbyLoop(Node node){ Stack<Node> stack = new Stack(); Node p = node; while(p!=null || !stack.isEmpty()){ while(p!=null){ stack.push(p); p = p.getLeft(); } if(!stack.isEmpty()){ p = stack.pop(); System.out.print(p.getValue()+" "); p = p.getRight(); } } } /** * 非递归后序遍历 * */ public static void postOrderTraversalbyLoop(Node node){ Stack<Node> stack = new Stack<Node>(); Node p = node, prev = node; while(p!=null || !stack.isEmpty()){ while(p!=null){ stack.push(p); p = p.getLeft(); } if(!stack.isEmpty()){ Node temp = stack.peek().getRight(); //只是拿出来栈顶这个值,并没有进行删除 if(temp == null||temp == prev){ //节点没有右子节点或者到达根节点【考虑到最后一种情况】 p = stack.pop(); System.out.print(p.getValue()+" "); prev = p; p = null; } else{ p = temp; } } } } // 广度优先遍历 参数node为根节点 public static void levelOrderTraversal(Node node){ if(node==null){ System.out.print("empty tree"); return; } ArrayDeque<Node> deque = new ArrayDeque<Node>(); deque.add(node); while(!deque.isEmpty()){ Node rnode = deque.remove(); System.out.print(rnode.getValue()+" "); if(rnode.getLeft()!=null){ deque.add(rnode.getLeft()); } if(rnode.getRight()!=null){ deque.add(rnode.getRight()); } } } // 深度优先遍历 参数node为根节点 public static void depthTraversal(Node node){ if(node==null){ System.out.print("empty tree"); return; } Stack<Node> stack = new Stack<Node>(); stack.push(node); while(!stack.isEmpty()){ Node rnode = stack.pop(); System.out.print(rnode.getValue()+" "); if(rnode.getLeft()!=null){ stack.add(rnode.getLeft()); } if(rnode.getRight()!=null){ stack.add(rnode.getRight()); } } } }
3.深度优先和广度优先遍历详细步骤
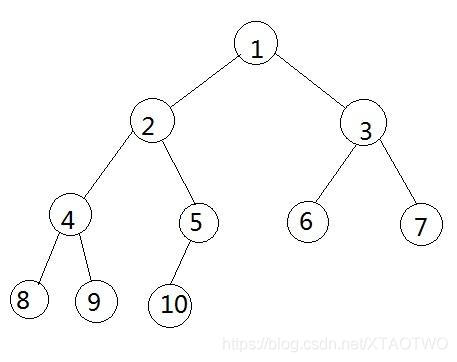
深度优先遍历:
深度优先遍历(Depth First Search),简称DFS,其原则是,沿着一条路径一直找到最深的那个节点,当没有子节点的时候,返回上一级节点,寻找其另外的子节点,继续向下遍历,没有就向上返回一级,直到所有的节点都被遍历到,每个节点只能访问一次。
上图中的深度优先遍历结果是 {1,2,4,8,9,5,10,3,6,7 },遍历过程是首先访问1,然后是1的左节点2,然后是2的左节点4,再是4的左节点8,8没有子节点了,返回遍历8的父节点的4的另一个子节点9,9没有节点,再向上返回。(注意:这里的返回上一次并不会去重新遍历一遍)。
在算法实现的过程中,我们采用了栈(Stack)这种数据结构,它的特点是,最先压入栈的数据最后取出。
算法步骤:
1、首先将根节点1压入栈中【1】
2、将1节点弹出,找到1的两个子节点3,2,首先压入3节点,再压入2节点(后压入左节点的话,会先取出左节点,这样就保证了先遍历左节点),2节点再栈的顶部,最先出来【2,3】
3、弹出2节点,将2节点的两个子节点5,4压入【4,5,3】
4、弹出4节点,将4的子节点9,8压入【8,9,5,3】
5,弹出8,8没有子节点,不压入【9,5,3】
6、弹出9,9没有子节点,不压入【5,3】
7、弹出5,5有一个节点,压入10,【10,3】
8、弹出10,10没有节点,不压入【3】
9、弹出3,压入3的子节点7,6【6,7】
10,弹出6,没有子节点【7】
11、弹出7,没有子节点,栈为空【】,算法结束
我们来看一看节点的出栈顺序【1,2,4,8,9,5,10,3,6,7】,刚好就是我们深度遍历的顺序。下面看Java代码
/** * 二叉树的深度优先遍历 * @param root * @return */ public List<Integer> dfs(Node root){ Stack<Node> stack=new Stack<Node>(); List<Integer> list=new LinkedList<Integer>(); if(root==null) return list; //压入根节点 stack.push(root); //然后就循环取出和压入节点,直到栈为空,结束循环 while (!stack.isEmpty()){ Node t=stack.pop(); if(t.getRight()!=null) stack.push(t.getRight()); if(t.getLeft()!=null) stack.push(t.getLeft()); list.add(t.getValue()); } return list; }
广度优先遍历:
广度优先遍历(Breadth First Search),简称BFS;广度优先遍历的原则就是对每一层的节点依次访问,一层访问结束后,进入下一层,直到最后一个节点,同样的,每个节点都只访问一次。
上图中,广度优先遍历的结果是【1,2,3,4,5,6,7,8,9,10】,遍历顺序就是从上到下,从左到右。
在算法实现过程中,我们使用的队列(Queue)这种数据结构,这种结构的特点是先进先出,在java中Queue是一个借口,而LinkedList实现了这个接口的所有功能。
算法过程:
1、节点1,插入队列【1】
2、取出节点1,插入1的子节点2,3 ,节点2在队列的前端【2,3】
3、取出节点2,插入2的子节点4,5,节点3在队列的最前端【3,4,5】
4、取出节点3,插入3的子节点6,7,节点4在队列的最前端【4,5,6,7】
5、取出节点4,插入3的子节点8,9,节点5在队列的最前端【5,6,7,8,9】
6、取出节点5,插入5的子节点10,节点6在队列的最前端【6,7,8,9,10】
7、取出节点6,没有子节点,不插入,节点7在队列的最前端【7,8,9,10】
8、取出节点7,没有子节点,不插入,节点8在队列的最前端【8,9,10】
9、取出节点8,没有子节点,不插入,节点9在队列的最前端【9,10】
10、取出节点9,没有子节点,不插入,节点10在队列的最前端【10】
11、取出节点10,队列为空,算法结束
我们看一下节点出队的顺序【1,2,3,4,5,6,7,8,9,10】,就是广度优先遍历的顺序,下面看java代码
/** * 二叉树的广度优先遍历 * @param root * @return */ public List<Integer> bfs(Node root) { Queue<Node> queue = new LinkedList<Node>(); List<Integer> list=new LinkedList<Integer>(); if(root==null) return list; queue.add(root); while (!queue.isEmpty()){ Node t=queue.remove(); if(t.getLeft()!=null) queue.add(t.getLeft()); if(t.getRight()!=null) queue.add(t.getRight()); list.add(t.getValue()); } return list; }
参考地址:
https://blog.csdn.net/weixin_42636552/article/details/82973190
https://blog.csdn.net/XTAOTWO/article/details/83625586