基本思想:
希尔排序就是对直接插入排序的一个优化。现在有一个array,希尔排序就是设定一个增量incrementNum(0<incrementNum<array.length)。先从array[0]开始,以incrementNum为增量的进行直接插入排序,直到数组末尾,然后从array[1]开始重复:以incrementNum为增量的进行直接插入排序; 然后从array[1]开始重复......一直到array[n]。然后取一个小于上一步增量的新的增量(比如设置为incrementNum/2),对前一个步骤的结果array进行遍历,直接插入排序....,再取小于上一步增量的新的增量,重复进行:遍历,直接插入排序直到新的增量小于1之后再退出循环。
过程:
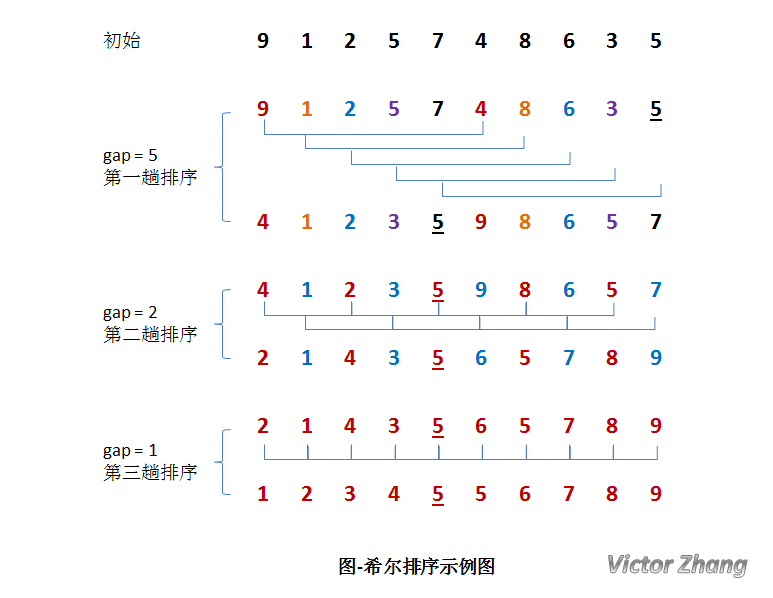
图片来自:http://www.cnblogs.com/jingmoxukong/p/4303279.html
Java代码实现:
public class Xier {
public static void Shellsort(int[] arrays){
if(arrays == null || arrays.length <= 1){
return;
}
//增量
int incrementNum = arrays.length/2;
while(incrementNum >=1){
for(int i=0;i<arrays.length;i++){
//进行插入排序
for(int j=i;j<arrays.length-incrementNum;j=j+incrementNum){
if(arrays[j]>arrays[j+incrementNum]){
int temple = arrays[j];
arrays[j] = arrays[j+incrementNum];
arrays[j+incrementNum] = temple;
}
}
}
//设置新的增量
incrementNum = incrementNum/2;
System.out.println(Arrays.toString(arrays));
}
}
public static void main(String[] args) {
int[] a = { 57, 68, 59, 52, 72, 28, 96, 33 };
Xier.Shellsort(a);
}
}
算法性能分析:
时间复杂度:最坏情况下为O(n^2),平均时间复杂度为O(nlogn)
空间复杂度:归并排序需要一个大小为1的临时存储空间用以保存合并序列,所以空间复杂度为O(1)
算法稳定性:从上面图片中可以看出,数字5在排序后交换了位置,所以它是不稳定的算法。