STEP1:首先了解规则与概念
威佐夫博弈(Wythoff's game):有两堆各若干个物品,两个人轮流从任一堆取至少一个或同时从两堆中取同样多的物品,规定每次至少取一个,多者不限,最后取光者得胜。
尼姆博弈(Nimm Game):有三堆各若干个物品,两个人轮流从某一堆取任意多的物品,规定每次至少取一个,多者不限,最后取光者得胜。
要注意,在威佐夫博弈中,玩家可以选择操作两堆物品,而在尼姆博弈中,只能对任意一堆物品进行操作。
STEP2:了解奇异局势
Q:什么是局势与奇异局势?
A:局势就是指当前所有堆的状态。奇异局势是指当一个玩家面对这种局势的时候且如果两个玩家都用最优秀的姿态博弈,那么进入奇异局势的玩家将不可能胜利,即进入必败态
(比如在我们知道的巴什博奕中,如果一个玩家面对的剩余数目为(最大拿取数目 + 1)的整数倍时(最多拿3个,剩16个),那么称16是一个奇异局势,在这种情况下,无论谁面对16这个数字,都一定必败)
Q:奇异局势有什么特点或者性质?
A:①任何自然数都包括在一个且仅存在一个的奇异局势中。
②任意操作(指的是在规则中出现的操作)都可以将一个奇异局势转化为一个非奇异局势。
③采用适当的操作,可以将一个非奇异局势转化为奇异局势。
STEP3:晦涩的推导与证明
以威佐夫博弈为背景来证明奇异局势的3个性质
我们使用诸如(a[k],b[k])(k = 0,1,2,3,4...,n)这种方法来定义局势,k表示奇异局势的序号, 第一个奇异局势k=0。
首先写出几个最开始的奇异局势:(0,0)(1,2)(3,5)(4,7)(6,10)(8,13)(9,15)(11,18)(12.20)......
一些机智的小伙伴一下子就能看出端倪了。
这些局势存在以下特点:
k0 = (a0,b0)(a0 == 0 && b0 == 0)
kn = (an,bn)(bn == an + n)
a[k]是前面所有奇异局势中没有出现过的且是最小的自然数。
那么上述几个性质自然得证:
性质①:
有a[k] > a[k-1] ,而 b[k]= a[k] + k > a[k-1] + k > a[k-1] + (k - 1) = b[k-1] > a[k-1] 。
性质②:
若我们只改变奇异局势(a[k],b[k])的某一个分量,那么另一个分量不可能在其他奇异局势中,所以必然是非奇异局势。
如果使(a[k],b[k])的两个分量同时减少,由于其差不变,而且所有的奇异局势的差值(bk-ak)都不相同,因此也是非奇异局势。
性质③:
若当前局势是b == a,则同时从两堆中取走所有物体,即变为奇异局势(0,0)。
若当前局势是a = a[k],b > b[k],那么,从第二堆取走b - b[k]个物体,即变为奇异局势(ak,bk)。
若当前局势是a = a[k],b < b[k],则同时从两堆中拿走a - a[b - a]个物体([b - a]是a的下标,不是a*(b - a)),即变为奇异局势(a[b - a],a[b - a] + (b - a))。
若当前局势是a > a[k],b = a[k] + k,则从第一堆中拿走多余的数量a - a[k] ,即变为奇异局势(ak,ak + k)。
若当前局势是a < a[k],b = a[k] + k,若a == aj(j < k)从第二堆里面拿走 b - bj 个物体,即变为奇异局势(可使用k3 = (4,7)与 k2 = (3,5)推导)。
若a == bj(j < k)从第二堆里面拿走 b - aj 个物体。即变为奇异局势(可使用k7 = (11,18)与 k4 = (6,10)推导)。
威佐夫博弈与尼姆博弈的具体证明暂时不贴了,去百度百科或各种dalao的博客查看即可。(溜了溜了)、
STEP4:如何判断给出局势是否为奇异局势
如何判断威佐夫博弈的奇异局势
其实对于任意一个k,ak是存在公式的:ak = (int)(k * (sqrt(5) + 1) / 2)。
有趣的事情发生了,这个数与黄金分割有关。其实在威佐夫博弈中,奇异局势的规律十分符合Beatty定理,ak与bk做边所构成的矩形是越来越接近黄金矩形的。
因此在给出了两个堆得物品数目时,只需要看这两个堆的差(也就是 bj - aj = j)的(sqrt(5) + 1) / 2)倍再取整,是否等于较少的一堆即可。
即(int)(abs(b - a) * (sqrt(5) + 1) / 2)) == min(a,b)时符合奇异局势。
如何判断尼姆博弈的奇异局势
对于任意局势(a,b,c),我们只需要判断 a^b^c(按位模二加,即抑或运算)的结果就可以了。
结果是0,那么这个局势就是一个奇异局势。
这个判断方法同样适用于扩展到n堆物品的尼姆博弈
STEP5:结论
在威佐夫博弈中
先手面对奇异局势必败(无论自己如何破坏奇异局势,对手都可将非奇异局势转化为奇异局势)。
相反地,先手面对非奇异局势必胜(转化为奇异局势即可)。
在尼姆博弈中
只需要把每一堆的值抑或,如果结果是0,那么先手必败,结果不是0,后手必败。
STEP6:例题以及参考代码
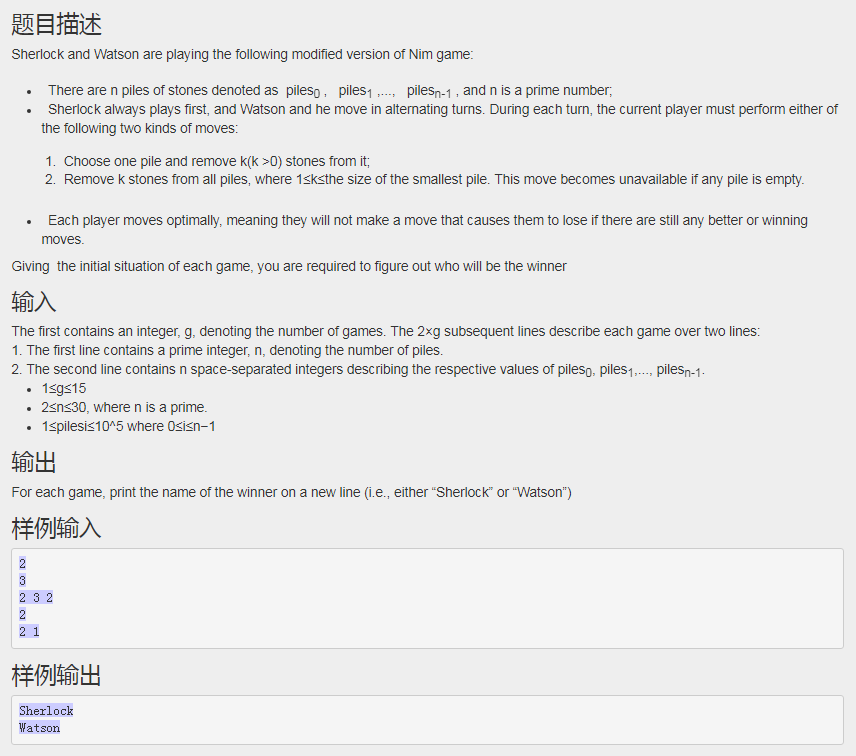
这道题其实就是个裸的博弈。n == 2的时候是威佐夫博弈,n >= 3的时候是尼姆博弈。
但是不知道当时为什么只有我们这个蒟蒻队伍出了,不知道其他dalao们是不是没开这道题。。。
放个代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 4 int main() 5 { 6 int T,n,m,k; 7 scanf("%d",&T); 8 while(T --){ 9 //while(scanf("%d",&n) != EOF){ 10 scanf("%d",&n); 11 if(n == 2){ 12 int a,b; 13 scanf("%d%d",&a,&b); 14 double c = abs(a - b) * ((sqrt(5.0) + 1.0) / 2.0); 15 int d = int(c); 16 if(d != min(a,b)){ 17 printf("Sherlock "); 18 } 19 else{ 20 printf("Watson "); 21 } 22 } 23 else{ 24 int ans = 0; 25 for(int i = 0;i < n;i ++){ 26 scanf("%d",&k); 27 if(i == 0){ 28 ans = k; 29 } 30 else{ 31 ans = ans ^ k; 32 } 33 } 34 if(ans == 0){ 35 printf("Watson "); 36 } 37 else{ 38 printf("Sherlock "); 39 } 40 } 41 } 42 return 0; 43 }
