[Leetcode] Construct binary tree from inorder and postorder travesal 利用中序和后续遍历构造二叉树

Given inorder and postorder traversal of a tree, construct the binary tree.

Note: 
 You may assume that duplicates do not exist in the tree.

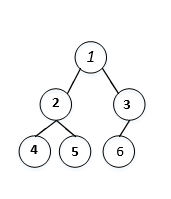
利用中序和后序遍历构造二叉树，要注意到后序遍历的最后一个元素是二叉树的根节点，而中序遍历中，根节点前面为左子树节点后面为右子树的节点。例如二叉树：{1,2,3,4,5,6,#}的后序遍历为4->5->2->6->3->1；中序遍历为：4->2->5->1->6->3。

故，递归的整体思路是，找到根节点，然后遍历左右子树。这里有一个很重要的条件是：树中没有重复元素。

方法一：递归

值得注意的是：递归过程中，起始点的选取。Grandyang对下标的选取有较为详细的说明。至于这个递归过程，（个人愚见，欢迎大神给出更好递归过程）可以在脑海想，构造顺序为4->5->2构建好左子树，接上1，然后6->3构建好右子树，最后接上1，完成。

/**
 * Definition for binary tree
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder) 
    {
        int len=inorder.size();
        return build(inorder,0,len-1,postorder,0,len-1);    
    }
    TreeNode *build(vector<int> &inorder,int inBeg,int inEnd,vector<int> &postorder,int postBeg,int postEnd)
    {
        if(inBeg>inEnd||postBeg>postEnd)    return NULL;
        TreeNode *root=new TreeNode(postorder[postEnd]);

        for(int i=0;i<inorder.size();++i)
        {
            if(inorder[i]==postorder[postEnd])
            {
                root->left=build(inorder,inBeg,i-1,postorder,postBeg,postBeg+i-1-inBeg);
                root->right=build(inorder,i+1,inEnd,postorder,postBeg+i-inBeg,postEnd-1);
            }
        }
        return root;    
    }
};

方法二：

利用栈。这个方法是以前看到出处也尴尬的忘了，分析过程等我再次看懂了再补上。这种方法改变了数组。

/**
 * Definition for binary tree
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder) 
    {
        if(inorder.size()==0)   return NULL;
        TreeNode* p;
        TreeNode* root;
        stack<TreeNode*> stn;

        root=new TreeNode(postorder.back());
        stn.push(root);
        postorder.pop_back();

        while(true)
        {
            if(inorder.back()==stn.top()->val)
            {
                p=stn.top();
                stn.pop();
                inorder.pop_back();

                if(inorder.size()==0)   break;
                if(stn.size()&&inorder.back()==stn.top()->val)
                    continue;
                
                p->left=new TreeNode(postorder.back());
                postorder.pop_back();
                stn.push(p->left);
            }
            else
            {
                p=new TreeNode(postorder.back());
                postorder.pop_back();
                stn.top()->right=p;
                stn.push(p);
            }
        }
        return root;
    }
};