本博文为博主自己对0-1背包问题的理解并结合网上的博客所写,因为个人水平有限,若是有错误的地方欢迎指出。谢谢!
- 问题描述:
给定n种物品和一个背包,物品i的重量是w[i],其价值为v[i],背包容量为cap,如何选择转入背包的物品,使得装入背包中的物品价值总最大?
- 问题归纳
对于某一种物品,要么装入背包,要么不装,我们将其状态取0-1,装入为1,不装为0,此问题称为0-1背包问题。
一、问题分析及代码实现
当w[ ]={2,2,6,5,4};v[ ]={6,3,5,4,6},背包容量cap=10时
1、新建一个二维数组dp[6][11],dp[i][j]为背包容量为j,第i个物品装入背包时的最大价值。
为什么要多一行一列了?因为这时要考虑,不往背包装物品和背包容量为0时的情况,此时。装入第一个物品时,只有当cap>=w[1],如下图:
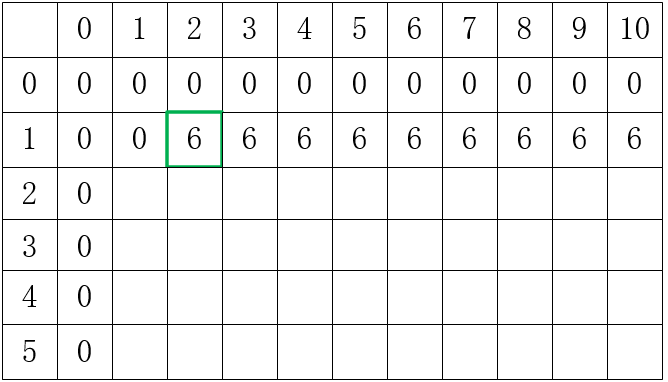
2、上图中,只有一个物品w[1 ],所以就算cap容量再大也只放一个,当装物品2时,只考虑1、2不考虑剩下的,只考虑已经装的和即将装入的价值。同理得到:
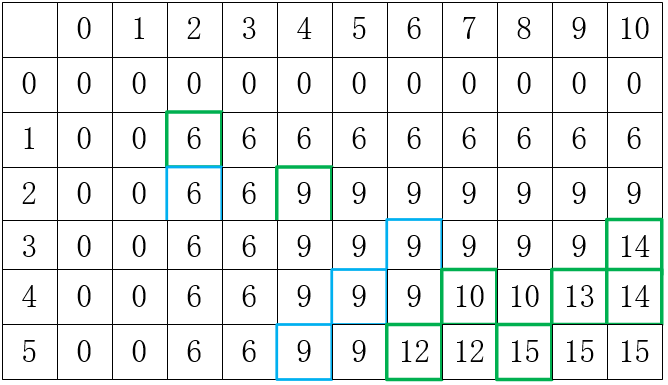
其中,蓝色的框表示,当考虑物品 i 时,虽然,此时背包容量等于w[ i ],但是其价值没有之前的同等容量下的价值大,所以维持不变。绿色表示,当此时背包的容量减去当前物品的重量以后,还有多余的容量,而多余的容量能装下的物品大的价值大与之前的方案,所以修改装入方案,使价值最大。
3、递推式:
当当cap<w[i],说明装不下当前的,那此时价值应该和之前的相同;当cap>=w[i],要考虑装入目前的了,多余的空间装入的价值和之前方案的价值的比较,若小于,则当前物品不用装入,若大于就装入;
1 dp= dp[i-1][j]; //当cap<w[i] 2 max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]); //当cap>=w[i]
4、代码实现:
1 /*说明: 2 *w[]为每个物体的重量,v[]为每个物体的价值,cap为背包的容量 3 */ 4 int Knapsack(const vector<int> &w,const vector<int> &v,const int cap) 5 { 6 int n=w.size(); //亦为物体的个数 7 vector<vector<int>> dp(n+1,vector<int>(cap+1,0)); 8 int i,j; 9 for(i=1;i<=n;i++) 10 { 11 for(j=1;j<=cap;j++) 12 { 13 dp[i][j]=dp[i-1][j]; 14 if(j>=w[i-1]) 15 { 16 dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i-1]); 17 } 18 } 19 } 20 return dp[n+1][cap+1]; 21 }
这里也可以用数组而不用向量,但因数组作为形参的时候,不能引入数组大小,函数要增加一个形参,所以图省事就用了向量。另外,这里代码中w[i-1]和v[i-1]之所以要减1,是因为二维矩阵中的下标与重量w[ ]和价值v[ ]的下标相差1要记得转换。
二、空间优化
注意到一点,就是每当我们计算dp[i][j]时,只用到了dp[i-1][0...j],因此,我们可以只用一个一维数组来实现上面的功能。
这里w[ ]={2,2,6,5,4};其下标不用转换。
1 int Knapsack(const vector<int> &w,const vector<int> &v,const int cap) 2 { 3 int n=w.size(); //亦为物体的个数 4 vector<int> dp(cap+1,0); 5 int i; 6 for(i=0;i<n;i++) 7 { 8 for(j=cap;j>=0;j--) 9 { 10 if(w[i]<j) 11 { 12 dp[j]=max(dp[j],dp[j-w[i]]+v[i]); 13 } 14 } 15 } 16 return dp[cap+1]; 17 }
值得注意的是:
dp[ ]是从右往左更新的,因为若是从左往右更新,其后的的值会受到之前已更新的值的影响,达不到不优化空间之间的访问上一行中元素的效果。这一点在很多优化动态规划算法的空间时都要注意。
Ref:
http://blog.csdn.net/kangroger/article/details/38864689
http://blog.csdn.net/dapengbusi/article/details/7463968
http://blog.csdn.net/stack_queue/article/details/53544109(背包九讲)