本文基于邓俊辉编著的《数据结构(C++语言版)(第3版)》和网上博文,仅介绍完全二叉树、满二叉树,平衡二叉树的相关概念。
一、二叉树
1、二叉树的概念
二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree),其次序不能任意颠倒。(百度百科)
2、性质
(1)若二叉树的层次从0开始,则在二叉树的第i层至多有2^i个结点(i>=0);
(2)高度为k的二叉树最多有2^(k+1) - 1个结点(k>=-1)。 (空树的高度为-1);
(3)对任何一棵二叉树,如果其叶子结点(度为0)数为m, 度为2的结点数为n, 则m = n + 1。
二、几种特殊的二叉树
1、满二叉树
所有叶结点同处于最底层(非底层结点均是内部结点),一个深度为k(>=-1)且有2^(k+1) - 1个结点。如图(图来源于veil的博客):
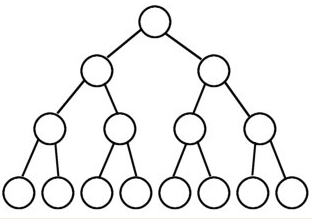
2、完全二叉树
叶结点只能出现在最底层的两层,且最底层叶结点均处于次底层叶结点的左侧。规模为n的完全二叉树,高度为
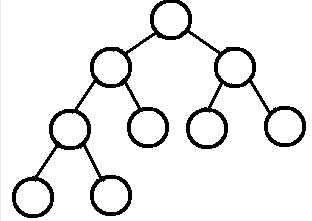
3、平衡二叉树
平衡二叉树(Self-balancing binary search tree)又被称为AVL树(有别于AVL算法),且具有以下性质:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。 最小二叉平衡树的节点的公式如下 F(n)=F(n-1)+F(n-2)+1 这个类似于一个递归的数列,可以参考Fibonacci(斐波那契)数列,1是根节点,F(n-1)是左子树的节点数量,F(n-2)是右子树的节点数量。(百度百科)
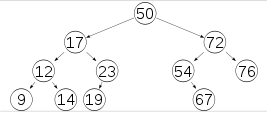
对于平衡二叉树要特别注意的是,不要求非叶节点都有两个子结点,仅要求两个子树的高度差的绝对值不超过1,或者为空树。
三、存储方式
存储的方式和图一样,有链表和数组两种,用数组存访问速度快,但插入、删除节点操作就比较费时了。实际中更多的是用链来表示二叉树的。
Ref: