【NOIp 2016】换教室

题目略

mdzz 关于这题，出锅不是题的错，是我脑残：

1.e和v读反了，e<=90000，v<=300。。。。。。

导致我一度以为floyd锅了！！！

2.dp(n,m-1,1),dp(n,m,0)忘加minn了。。。。

然后编译器还没开Wall，没报错，竟然真跑出来了个结果！！！

还很接近，搞得我还以为我精度出锅了，甚至一度怀疑人生地换成io流读入。。。

3.忘了m可以等于0 。。。。。。

总之，脑残不要紧，至少方程秒出。。。还算比较欣慰：

数据范围看一眼v<=300，还要最短路。。。

果断floyd O(n^3)预处理出所有点对最短距离

然后，划分一下阶段，就是个傻dp

方程很好写出（就是有点长，自己感受一下）：

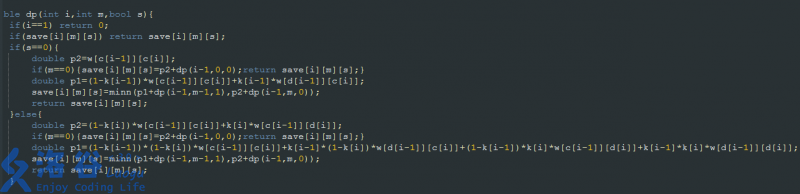
思路倒是很简单：期望线性性( E(x+y)=E(x)+E(y) )瞎搞一下就可以了，搞成阶段式：

d(i,m,s) i代表前i门课，m代表剩下的申请数，s表示i换不换

每条边都只与两相邻课程的交换概率有关，分类讨论一下就可以了。

要记忆化！

附代码：

#include<cstdio>
#include<cstring>
#define INF 0x3f3f3f
#define minn(a,b) (a)<(b)?(a):(b)
#define li for(i=1;i<=n;++i)
int n,m,e,v;
int w[301][301];
int c[2001],d[2001];
double k[2001],save[2001][2001][2];
template<typename T>
inline void read(T &x){
  char ch;while((ch=getchar()),(ch>'9'||ch<'0'));
  x=ch-'0';while((ch=getchar()),(ch>='0'&&ch<='9')) x=x*10+ch-'0';
}
double dp(int i,int m,bool s){
    if(i==1) return 0;
    if(save[i][m][s]) return save[i][m][s];
    if(s==0){
        double p2=w[c[i-1]][c[i]];
        if(m==0){save[i][m][s]=p2+dp(i-1,0,0);return save[i][m][s];}
        double p1=(1-k[i-1])*w[c[i-1]][c[i]]+k[i-1]*w[d[i-1]][c[i]];
        save[i][m][s]=minn(p1+dp(i-1,m-1,1),p2+dp(i-1,m,0));
        return save[i][m][s];
    }else{
        double p2=(1-k[i])*w[c[i-1]][c[i]]+k[i]*w[c[i-1]][d[i]];
        if(m==0){save[i][m][s]=p2+dp(i-1,0,0);return save[i][m][s];}
        double p1=(1-k[i-1])*(1-k[i])*w[c[i-1]][c[i]]+k[i-1]*(1-k[i])*w[d[i-1]][c[i]]+(1-k[i-1])*k[i]*w[c[i-1]][d[i]]+k[i-1]*k[i]*w[d[i-1]][d[i]];
        save[i][m][s]=minn(p1+dp(i-1,m-1,1),p2+dp(i-1,m,0));
        return save[i][m][s];
    }
}
int main(){
    freopen("classrooma6.in","r",stdin);
    read(n),read(m),read(v),read(e);
    register int i,a,b,t;
    li read(c[i]);
    li read(d[i]);
    li scanf("%lf",&k[i]);
    memset(w,INF,sizeof w);
    for(i=1;i<=e;++i){
        read(a),read(b),read(t);
        if(a==b) continue;
        if(w[a][b]==INF) w[a][b]=w[b][a]=t;
        else w[a][b]=w[b][a]=minn(w[a][b],t);
    }
    for(int t=1;t<=v;++t)
        for(a=1;a<=v;++a)
            for(b=1;b<=v;++b)
                w[a][b]=minn(w[a][b],w[a][t]+w[t][b]);
    for(int t=1;t<=v;++t) w[t][t]=0;
    double ans=dp(n,m,0);
    if(m!=0) ans=minn(ans,dp(n,m-1,1));
    printf("%.2lf",ans);
}