课程作业01
(1)使用组合数公式利用n!来计算
程序设计思想:
(大数据整数)
先定义一个取值上标和下标的函数得到n和k,和阶乘的函数;
通过阶乘函数返回得到n!、k!、(n-k)!(其中均为大数据整数的计算方法);
计算n!/[k!*(n-k)!];
程序流程图:
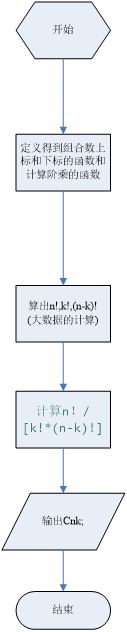
源程序代码:
import java.util.Scanner;
import java.math.BigInteger;
public class Combinatorics {
int n;//组合数的下标
int k;//组合数的上标
public static void main(String[] args) {
// TODO Auto-generated method stub
Combinatorics c=new Combinatorics();
c.getBiao();
BigInteger x,y,z,C,d;//定义大数据整数
x=c.jiecheng(c.n);//得到n!
y=c.jiecheng(c.k);//得到k!
z=c.jiecheng(c.n-c.k);//得到(n-k)!
d=y.multiply(z);//计算k!*(n-k)!
C=x.divide(d);//计算n!/[k!*(n-k)!]
System.out.println("组合数Cnk="+C);
}
public void getBiao()//得到组合数的上标和下标
{
System.out.println("请输入组合数的下标和上标:");
Scanner scanner=new Scanner(System.in);
n=scanner.nextInt();//输入下标
k=scanner.nextInt();//输入下标
}
public BigInteger jiecheng(int n0)//计算输入的整数的阶乘
{
BigInteger ji=BigInteger.ONE;//定义大数据整数ji
for(int i=1;i<=n0;i++)//循环可得到n0!
{
ji=ji.multiply(BigInteger.valueOf(i));
}
return ji;//返回积
}
}
程序截图:

(2)使用递推的方法用杨辉三角形计算
程序设计思想:
先输入组合数的上标和下标,定义二维数组方便存放数据;
初始化二维数组最开始的几个值,方便递推运算;
利用递推关系得到赋予二维数组值;
组合数Cnk就等于c[n][k].
程序流程图:
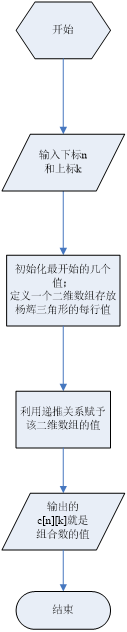
源程序代码:
import java.math.BigInteger;
import java.util.Scanner;
public class Combinatorics {
public static int n;//组合数的下标
public static int k;//组合数的上标
public static int c[][]=new int[100][100];//定义二维数组
public static void main(String[] args) {
// TODO Auto-generated method stub
System.out.println("请输入组合数的下标和上标:");
Scanner scanner=new Scanner(System.in);
n=scanner.nextInt();//输入下标
k=scanner.nextInt();//输入上标
c[0][0]=1;//初始化
c[1][0]=1;//初始化
c[1][1]=1;//初始化
for(int i=2;i<=n;i++)
{
c[i][0]=1;//当k=0时
c[i][i]=1;//当k=n时
for(int j=1;j<=i;j++)
{
c[i][j]=c[i-1][j-1]+(c[i-1][j]);//递推
}
}
System.out.println("组合数Cnk="+c[n][k]);//输出Cnk的值
}
}
程序截图:
(3)使用递归的方法用组合数递推公式计算
程序设计思想
先输入组合数的上标和下标,定义二维数组方便存放数据;
定义递归函数;
初始化二维数组最开始的几个值,用递归函数完成递推运算,赋予二维数组值;
组合数Cnk就等于c[n][k].
程序流程图:
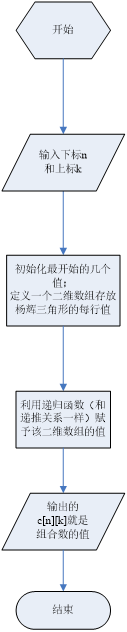
源程序代码:
import java.util.Scanner;
public class Combinatorics {
int n;//组合数的下标
int k;//组合数的上标
int c[][]=new int[100][100];
public static void main(String[] args) {
// TODO Auto-generated method stub
Combinatorics m=new Combinatorics();//构造函数
System.out.println("请输入组合数的下标和上标:");
Scanner scanner=new Scanner(System.in);
m.n=scanner.nextInt();//输入下标
m.k=scanner.nextInt();//输入上标
m.c[0][0]=1;//初始化
m.c[1][0]=1;//初始化
m.c[1][1]=1;//初始化
m.c[m.n][m.k]=m.digui(m.n,m.k);//调用递归函数
System.out.println("组合数C"+"("+m.n+")"+"("+m.k+")"+"="+m.c[m.n][m.k]);//输出组合数Cnk
}
public int digui(int n0,int k0)//递归函数
{
if(k0==n0 || k0==0){
return 1;//返回值
}
c[n0][k0]=digui(n0-1,k0)+digui(n0-1,k0-1);
return c[n0][k0];//返回值
}
}
程序截图:
课后作业2(汉诺塔)
程序设计思想:
调用递归函数hanoi,其终止条件为hanoi函数的参数n的值为1;
此程序只是输出移动的方案。
程序流程图:
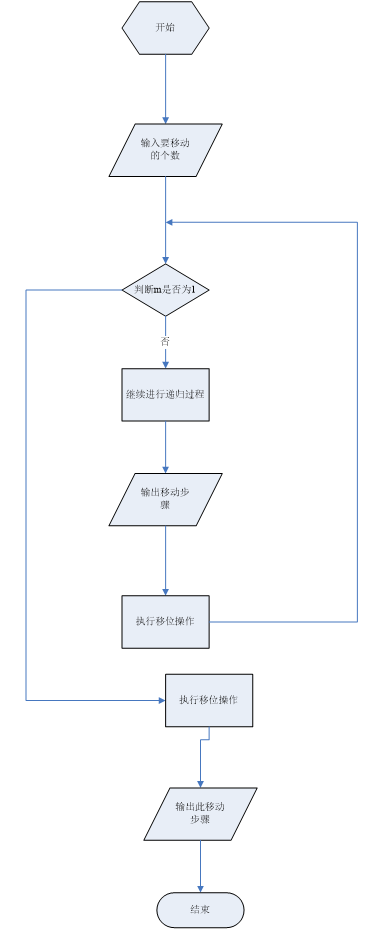
源程序代码:
import java.util.Scanner;
public class Hannuota {
public static void main(String[] args) {
// TODO Auto-generated method stub
Hannuota h=new Hannuota();//定义一个引用函数
int m;//要挪动的个数
System.out.print("请输入要挪动的个数:");
Scanner scanner=new Scanner(System.in);
m=scanner.nextInt();//输入m
System.out.println("移动的步骤为:");
h.hanoi(m,"peg1","peg2","peg3");//调用hanoi函数
}
public void hanoi(int n,String one,String two,String three)
{//将n个盘从one座借助two座,移到three座
if(n==1)
{
System.out.println(one+"->"+three);//输出该步骤
}
else
{
hanoi(n-1,one,three,two);//调用自己
System.out.println(one+"->"+three);
hanoi(n-1,two,one,three);
}
}
}
程序截图:
课后作业3
程序设计思想:
先输入要判断的字符串;
定义递归函数(其中是判断action是否等于over,若是则返回true(回文字符串),否则继续调用自己返回值);
最后判断返回值,看是否是字符串。
程序流程图:
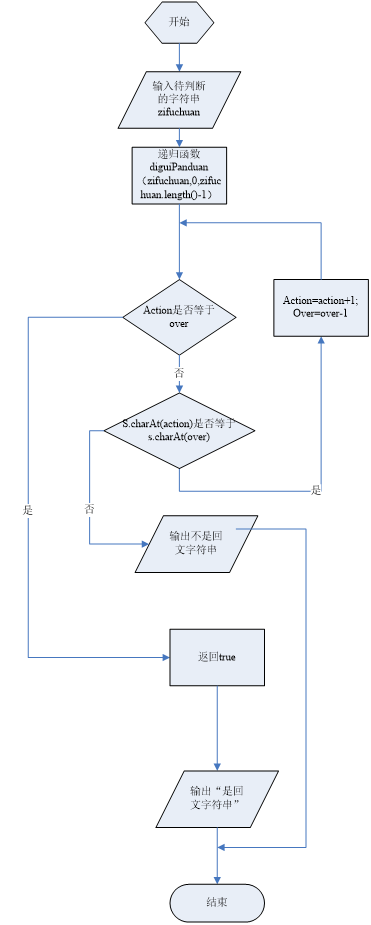
源程序代码:
import java.util.Scanner;
public class Huiwen {
public static void main(String[] args) {
// TODO Auto-generated method stub
Huiwen h=new Huiwen();//定义一个引用
String zifuchuan="";
System.out.print("输入你要进行判断的字符串:");
Scanner sr=new Scanner(System.in);
zifuchuan=sr.next();//输入要判断的字符串
int i=zifuchuan.length();//字符串的长度
boolean b=h.diguiPanduan(zifuchuan,0,i-1);//对递归函数的调用,将返回值赋予b
if(b==true)//判断布尔类型b
{
System.out.println("该字符串是回文字符串");
}
else
{
System.out.println("该字符串不是回文字符串");
}
}
public boolean diguiPanduan(String s,int action,int over)//递归函数
{
if(action==over)
{
return true;//返回值
}
else if(s.charAt(action)==s.charAt(over))//判断字符是否相等
{
return diguiPanduan(s,action+1,over-1);//对自身的调用
}
else
{
return false;//返回值
}
}
}
程序截图: