查找
统计多本书中每个单词出现的频率,使用符号表(字典),但是怎么快速定位到Key是一个难题,当Key数据量上亿了之后还能快速定位吗
查找的成本模型:比较次数,数组的访问次数
字典
public interface ISearchDict<TKey, TValue> : IDisposable
{
bool IsEmpty { get; }
int Length { get; }
bool Contains(TKey key);
TValue this[TKey key] { get;set; }
TValue Get(TKey key);
void Add(TKey key, TValue value);
void Delete(TKey key);
}
无序链表字典顺序查找
值得注意的是:这边使用递归实现删除,这个设计非常巧妙
public class SequentialSearchSTNet<TKey, TValue> : ISearchDict<TKey, TValue>
{
private int _length;
private Node _first;
private class Node:IDisposable
{
public TKey Key { set; get; }
public TValue Value { set; get; }
public Node Next { set; get; }
public Node(TKey key,TValue value,Node next)
{
Key = key;
Value = value;
Next = next;
}
public void Dispose()
{
Dispose(true);
}
protected virtual void Dispose(bool disposing)
{
if(disposing)
{
Key = default;
Value = default;
}
}
}
public SequentialSearchSTNet()
{
_length = 0;
_first = null;
}
public bool IsEmpty => _length==0;
public int Length => _length;
public void Add(TKey key, TValue value)
{
if (key == default || value == default) throw new ArgumentNullException("this key or value is default value");
if(_first!=null)
{
for (Node x = _first; x != null; x = x.Next)
{
if (key.Equals(x.Key))
{
x.Value = value;
return;
}
}
}
_first = new Node(key, value, _first);
_length++;
}
public bool Contains(TKey key)
{
if (key == default) throw new ArgumentNullException(" this key is default value");
if(!IsEmpty)
{
for(Node x=_first;x!=null;x=x.Next)
{
if(key.Equals(x.Key))
{
return true;
}
}
}
return false;
}
public TValue Get(TKey key)
{
if (key == default||IsEmpty) return default;
for(var x =_first;x!=null;x=x.Next)
{
if (key.Equals(x.Key))
return x.Value;
}
return default;
}
public TValue this[TKey key] { get => Get(key); set => Add(key,value); }
public void Delete(TKey key)
{
if (key == default) throw new ArgumentNullException(" this key is default value");
_first = delete(_first, key);
}
/// <summary>
/// 通过递归实现删除结点,这个设计非常巧妙
/// </summary>
/// <param name="x"></param>
/// <param name="key"></param>
/// <returns></returns>
private Node delete(Node x,TKey key)
{
if (x == null) return null;
if(key.Equals(x.Key))
{
_length--;
return x.Next;
}
x.Next = delete(x.Next, key);//这边非常巧妙的跳过了当前个,delete方法如果next是要删除对象就返回了x.next.next,如果不是就返回x.next;
return x;
}
public void Dispose()
{
Dispose(true);
}
protected virtual void Dispose(bool disposing)
{
if (disposing)
{
if (!IsEmpty)
{
for (var x = _first; x != null; x = x.Next)
{
x.Dispose();
}
_length = 0;
_first = null;
}
}
}
}
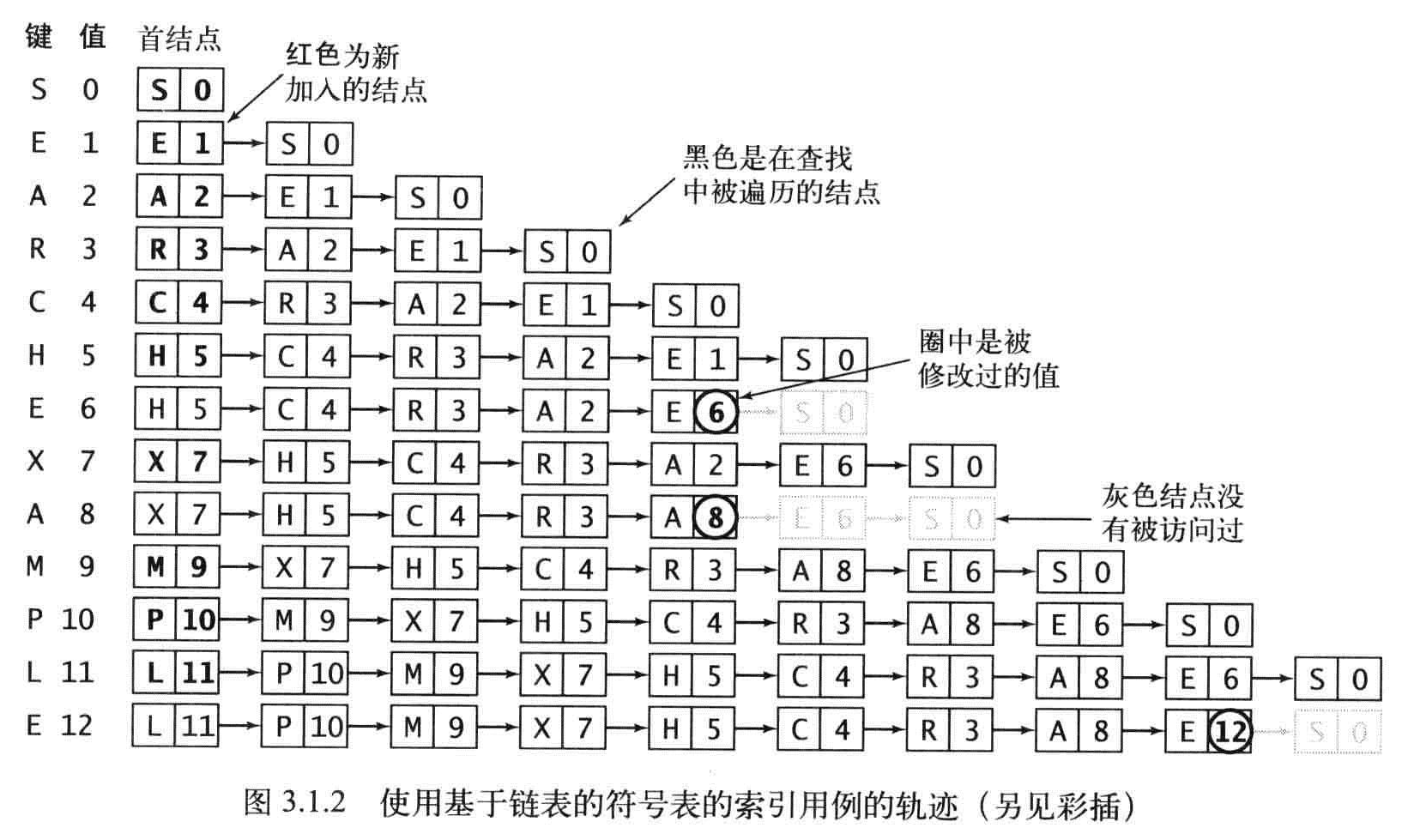
命题A:在含有N对键值的基于(无序)链表的符号表中,未命中的查找和插入操作都需要N次比较。命中的查找在最坏情况下需要N次比较。特别的,向一个空表插入N个不同的键需要~N^2/2次比较。
推论:向一个空表中插入N个不同的键需要~N^2/2次比较。
有序数组字典二分查找
有序字典的查找效率肯定高的多。
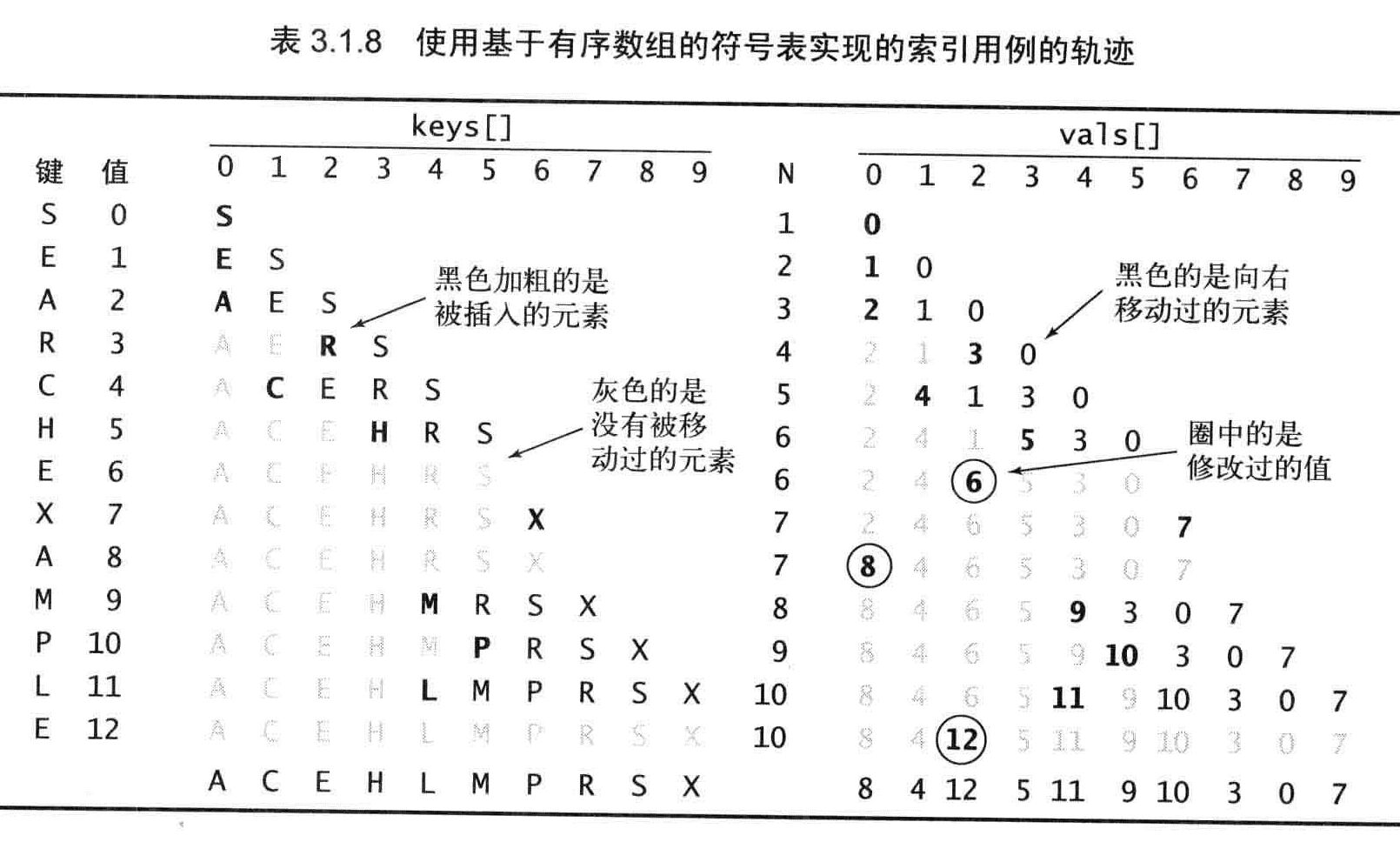
public interface IBinarySearchDict<TKey,TValue>: ISearchDict<TKey, TValue>
{
int Capacity { get; }
/// <summary>
/// 找到key对应的Index
/// </summary>
/// <param name="key"></param>
/// <returns></returns>
int Rank(TKey key);
void DeleteMin();
void DeleteMax();
TKey Min();
TKey Max();
TKey Floor(TKey key);
TKey Ceiling(TKey key);
}
public class BinarySearchSTNet<TKey, TValue> : IBinarySearchDict<TKey, TValue> where TKey : IComparable
{
private int _length;
private int _capacity;
private TKey[] _keys;
private TValue[] _values;
public BinarySearchSTNet():this(2)
{
}
public BinarySearchSTNet(int capacity)
{
_capacity = capacity;
_keys = new TKey[capacity];
_values = new TValue[capacity];
_length = 0;
}
public TValue this[TKey key] { get => Get(key); set => Add(key,value); }
public bool IsEmpty => _length==0;
public int Length => _length;
public int Capacity => _capacity;
private void resize(int capacity)
{
if (capacity < _length)
throw new ArgumentException("this capacity is less than length");
var temkey = new TKey[capacity];
var temvalue = new TValue[capacity];
for(int i=0;i<_length;i++)
{
temkey[i] = _keys[i];
temvalue[i] = _values[i];
}
_keys = temkey;
_values = temvalue;
}
public void Add(TKey key, TValue value)
{
if (key == default)
throw new ArgumentException("this key is default");
if (value == default)
{
Delete(key);
return;
}
int i = Rank(key);
if(i<_length && _keys[i].CompareTo(key)==0)
{
_values[i] = value;
}
if (_length == _keys.Length) resize(2 * _keys.Length);
for (int j = _length; j > i; j--)
{
_keys[j] = _keys[j - 1];
_values[j] = _values[j - 1];
}
_keys[i] = key;
_values[i] = value;
_length++;
}
public bool Contains(TKey key)
{
if (key == default||IsEmpty)
return false;
int i = Rank(key);
if (i < _length && key.CompareTo(_keys[i]) == 0)
return true;
return false;
}
public void Delete(TKey key)
{
if (key == default)
return;
if(Contains(key))
{
int i = Rank(key);
for(int j=i;j<_length-1;j++)
{
_keys[j] = _keys[j + 1];
_values[j] = _values[j + 1];
}
_keys[_length - 1] = default;
_values[_length - 1] = default;
_length--;
if (_length>0&&_length == _keys.Length / 4) resize(_keys.Length / 2);
}
}
public void DeleteMax()
{
if (!IsEmpty)
Delete(Max());
}
public void DeleteMin()
{
if (!IsEmpty)
Delete(Min());
}
public void Dispose()
{
throw new NotImplementedException();
}
protected virtual void Dispose(bool disposing)
{
if(disposing)
{
if(!IsEmpty)
{
for(int i=0;i<_length;i++)
{
_keys[i] = default;
_values[i] = default;
}
_length = 0;
_keys = null;
_values = null;
}
}
}
public TKey Ceiling(TKey key)
{
if (key == default)
return default;
int i = Rank(key);
if (i == _length) return default;
return _keys[i];
}
public TKey Floor(TKey key)
{
if (key == default)
return default;
int i = Rank(key);
if (i < _length && key.CompareTo(_keys[i]) == 0) return _keys[i];
if (i == 0) return default;
return _keys[i - 1];
}
public TValue Get(TKey key)
{
if (key == default || IsEmpty)
return default;
int i = Rank(key);
if (i < _length && _keys[i].CompareTo(key) == 0) return _values[i];
return default;
}
public TKey Max()
{
if (!IsEmpty)
return _keys[_length - 1];
return default;
}
public TKey Min()
{
if (!IsEmpty)
return _keys[0];
return default;
}
/// <summary>
/// 秩,key所在的等级,使用迭代
/// </summary>
/// <param name="key"></param>
/// <returns></returns>
public int Rank(TKey key)
{
if (key == default)
throw new ArgumentException("this key is default");
int lo = 0;
int hi = _length - 1;
while(lo<=hi)
{
int mid = lo + (hi - lo) / 2;
int cmp = key.CompareTo(_keys[mid]);
if (cmp < 0) hi = mid - 1;
else if (cmp > 0) lo = mid + 1;
else return mid;
}
return lo;
}
}
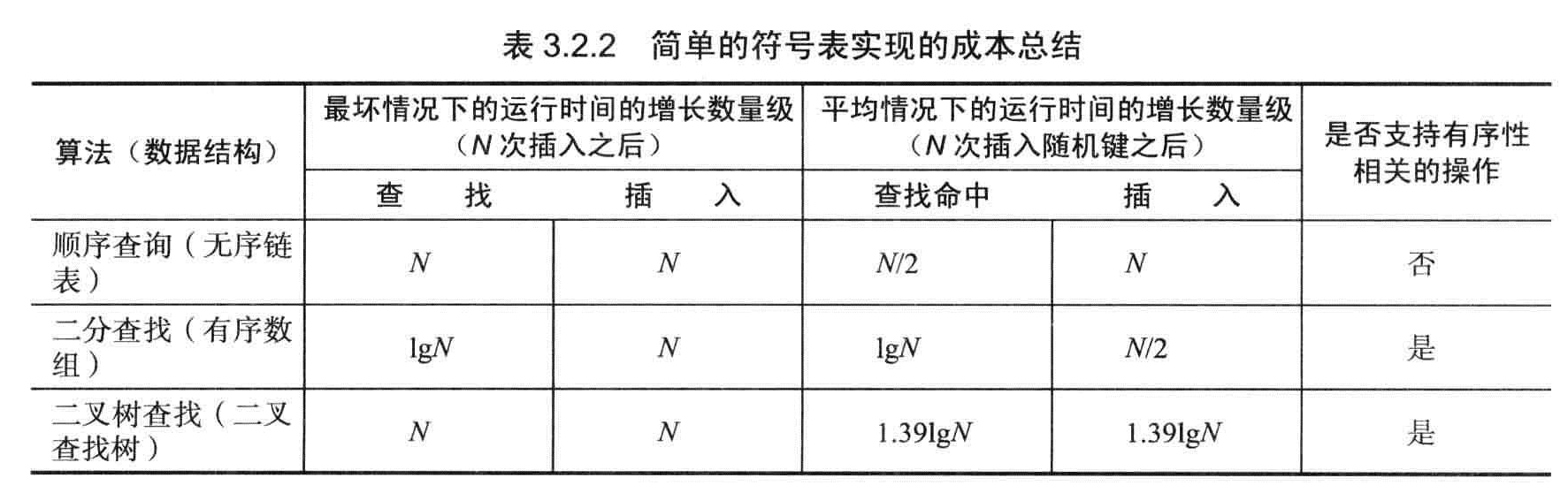
命题B:在N个键的有序数组中进行二分查找最多需要(lgN+1)次比较(无论是否成功)。

缺点:Add太慢了,基于有序数组的字典所需要访问数组的次数是数组长度的平方级别。
命题B(续):向大小为N的有序数组中插入一个新的元素在最坏情况下需要访问2N次数组,向空字典中插入N个元素在最坏情况下需要访问N^2次数组。
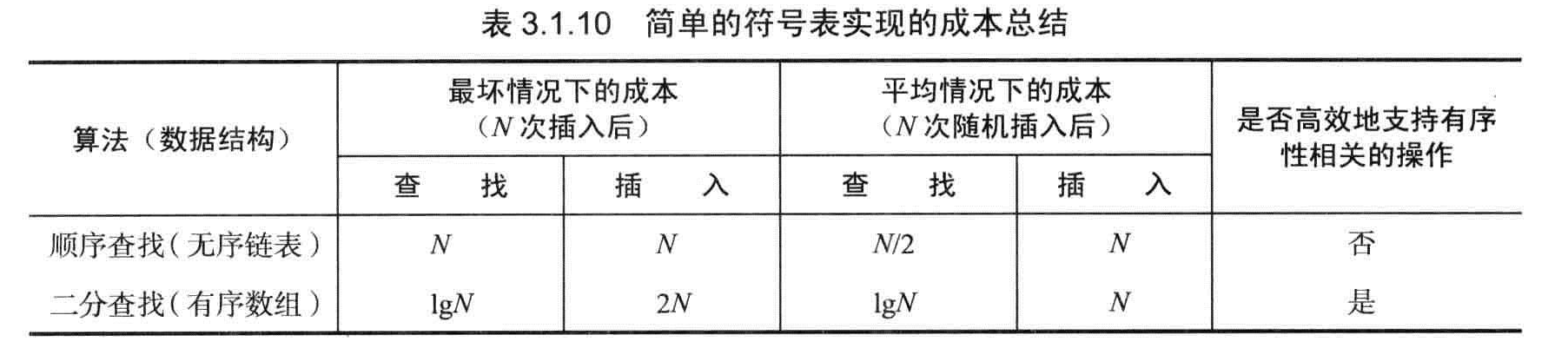
查找是LgN是目标之一,但是插入是2N似乎代价太大了,要支持高效的插入,似乎链式结构可以满足,但是链式结构是无法使用二分查找的。那么二叉查找树似乎就是我们一直追寻的目标。
二叉查找树
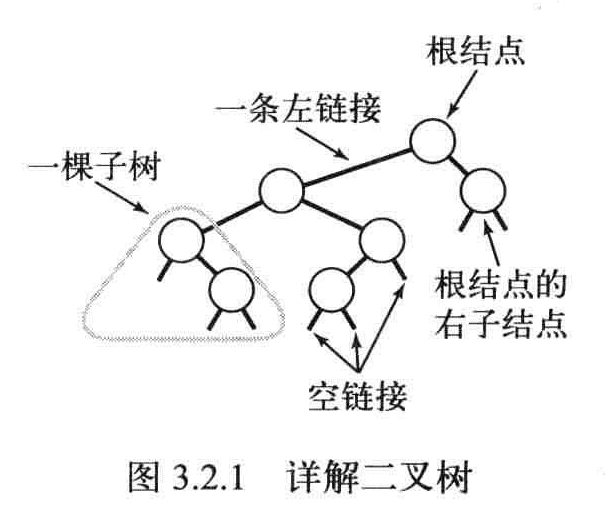
二叉树中,每个结点只有一个父结点指向自己,每个结点都只有左右两个链接。分别指向左子结点和右子结点。
二叉树的定义:每个结点都含有一个Comparable的键(以及相关联的值)且每个结点的键都大于其左子树中的任意结点的键而小于右子树的任意结点的键。
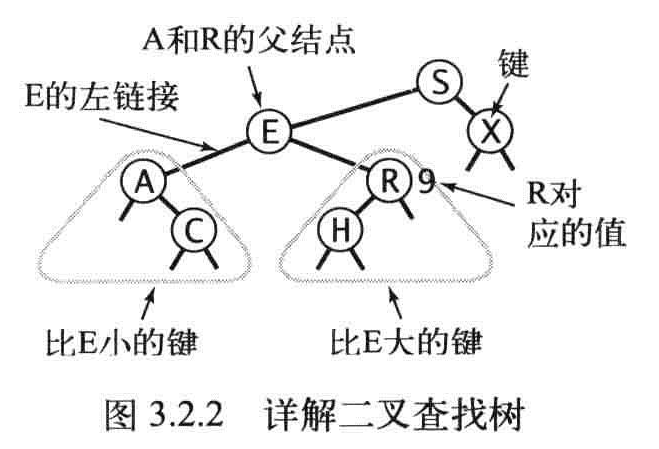
计数器
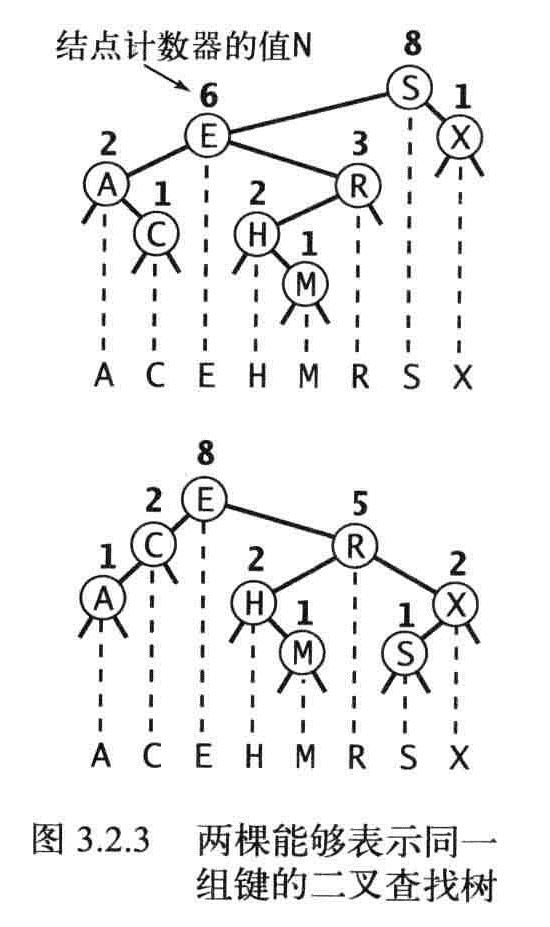
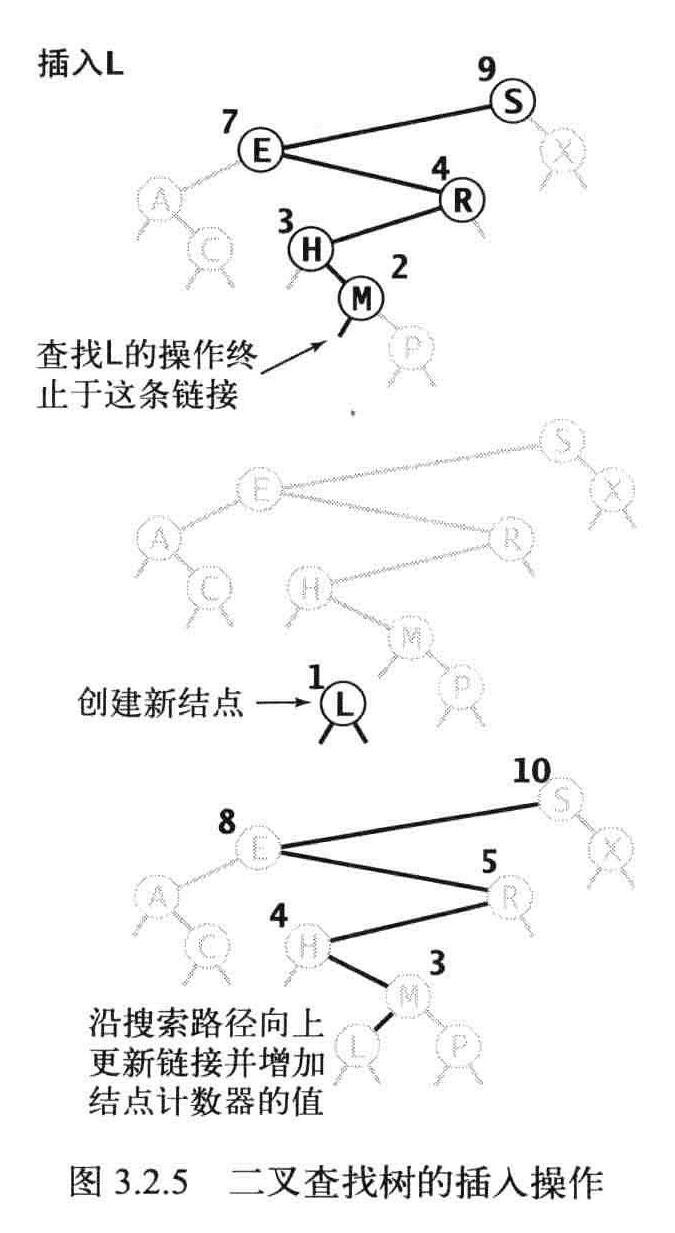
插入
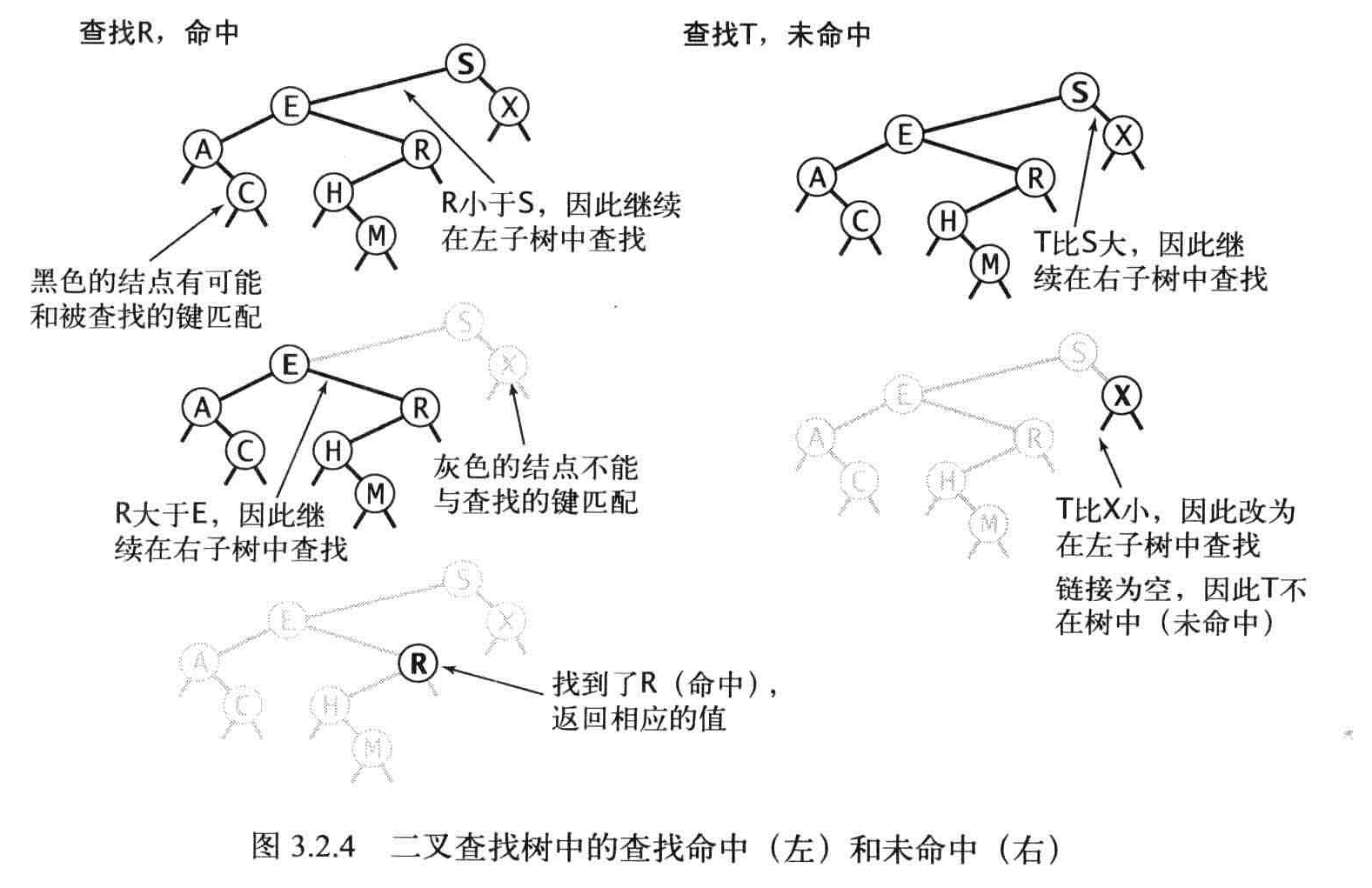
查找
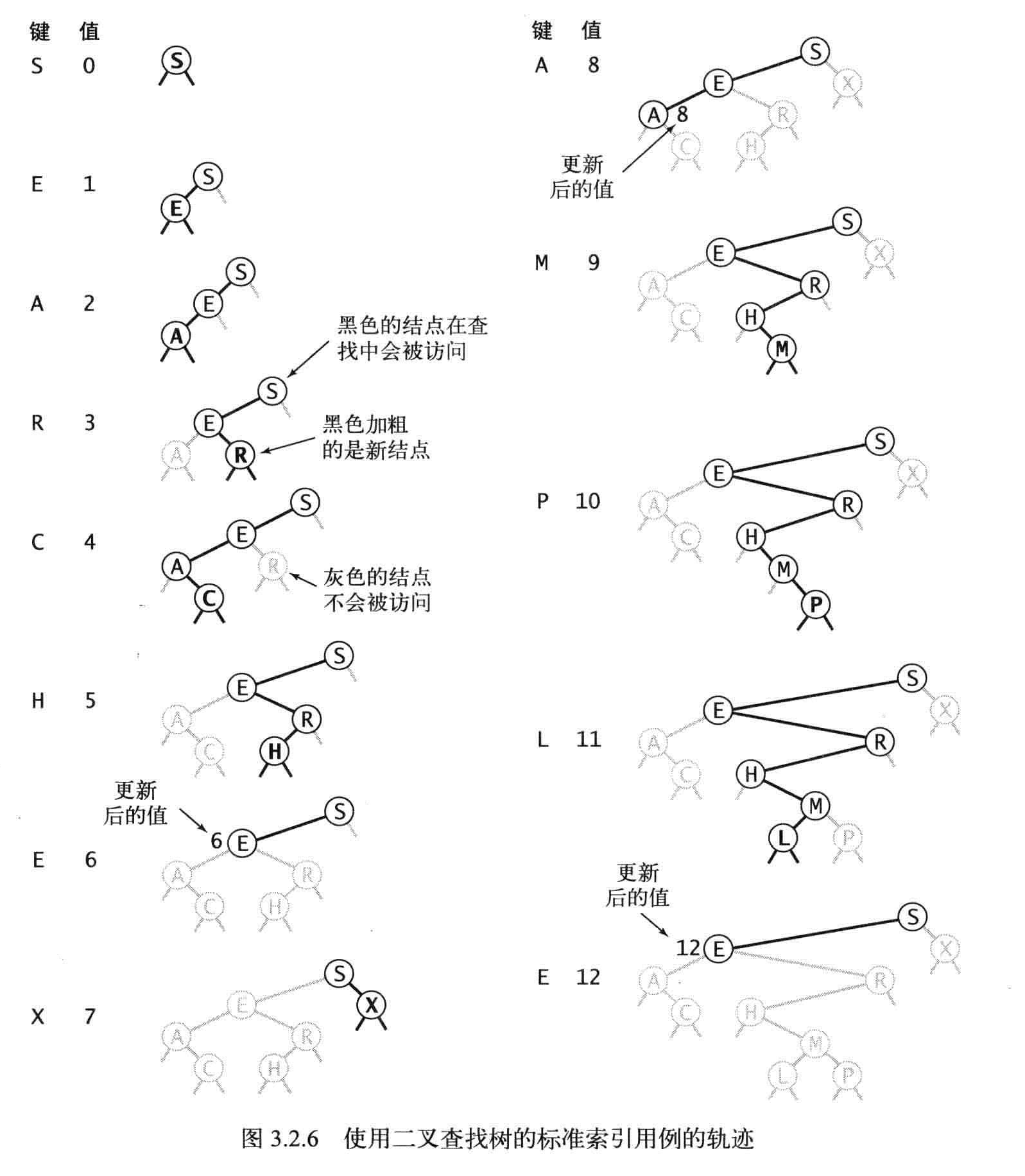
最好和最坏的情况
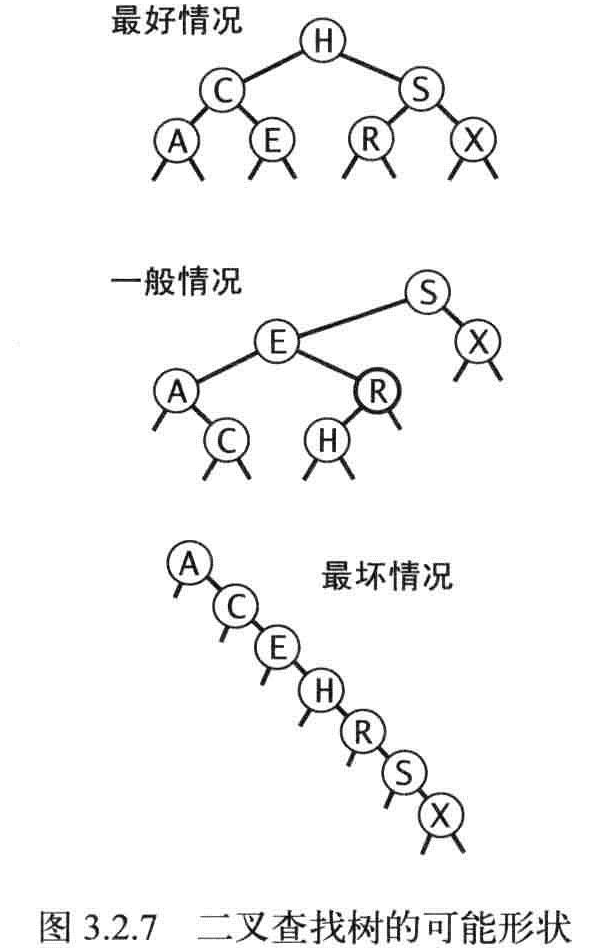
命题C:在由N个随机键构造的二叉查找树,查找命中平均所需的比较次数为~2InN(约1.39lgN)
命题D:在由N个随机键构造的二叉查找树中插入操作和查找未命中平均所需的比较次数未~2InN(1.39lgN).
Floor
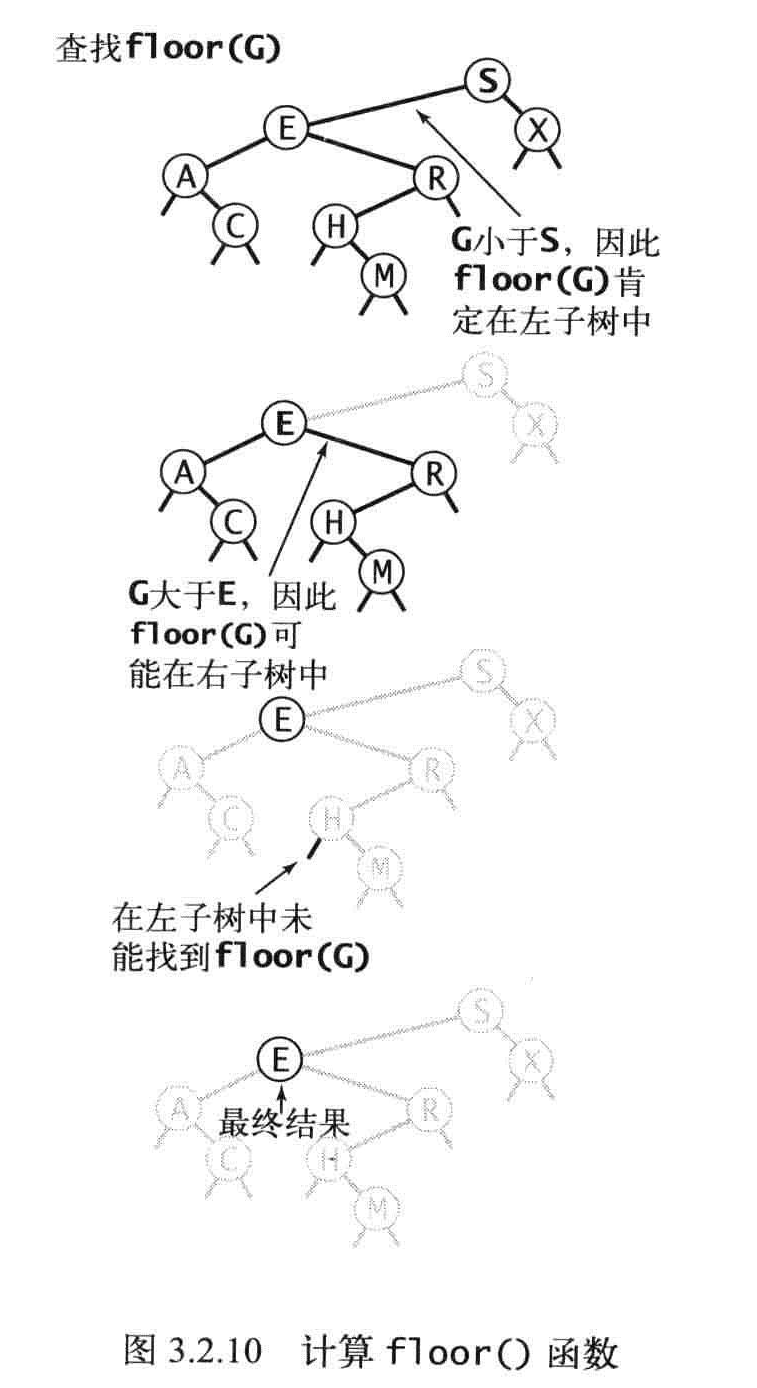
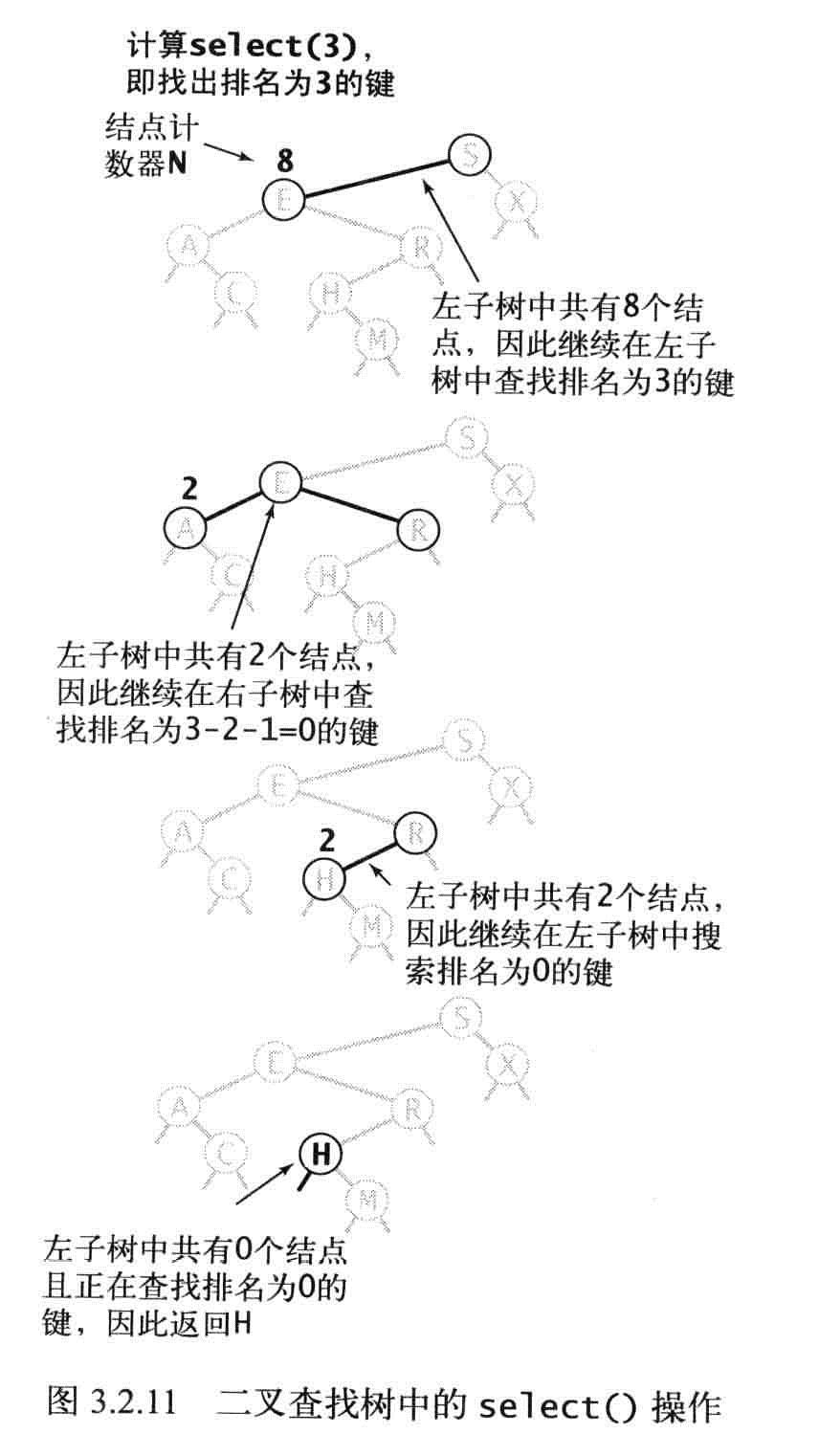
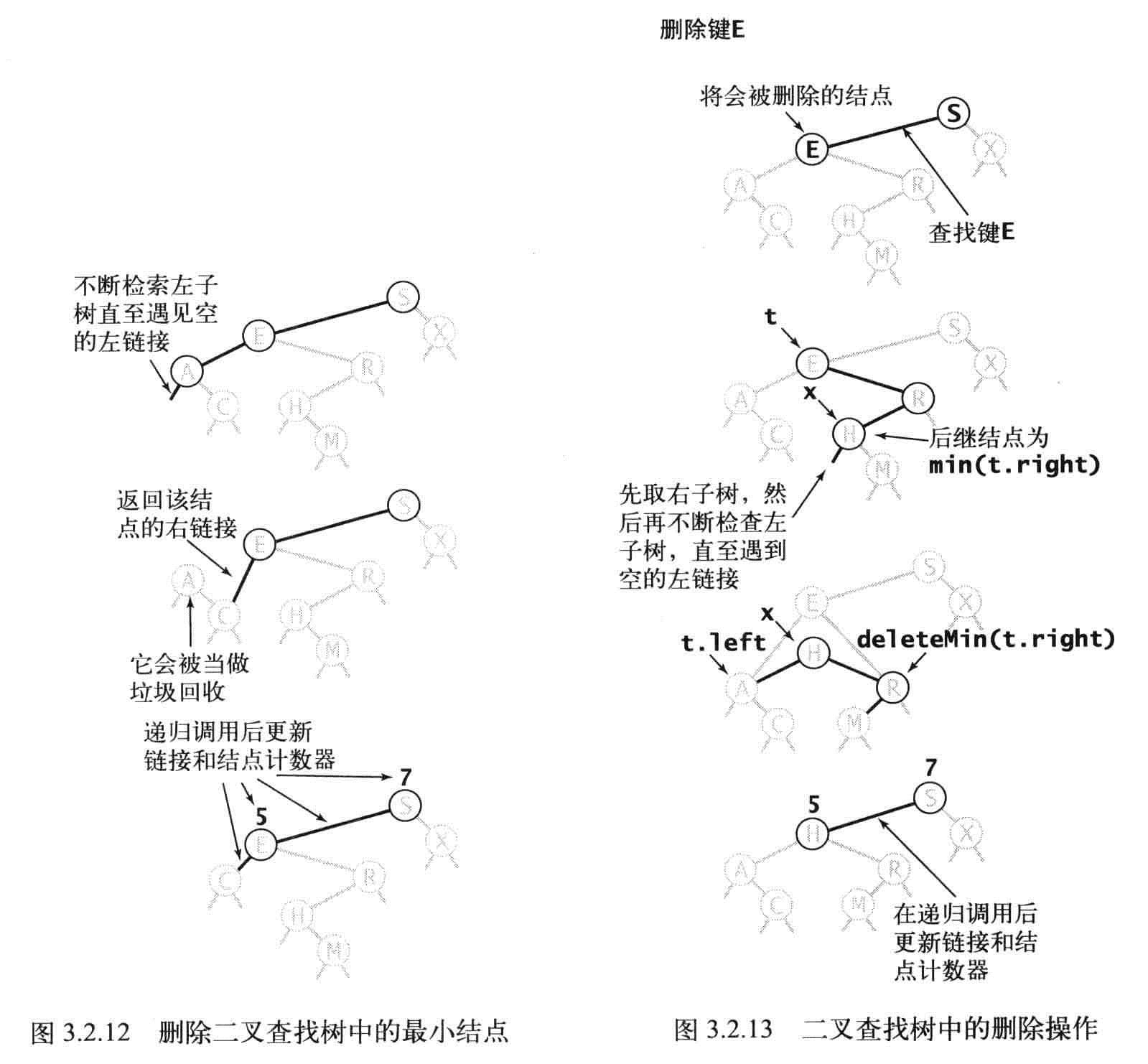
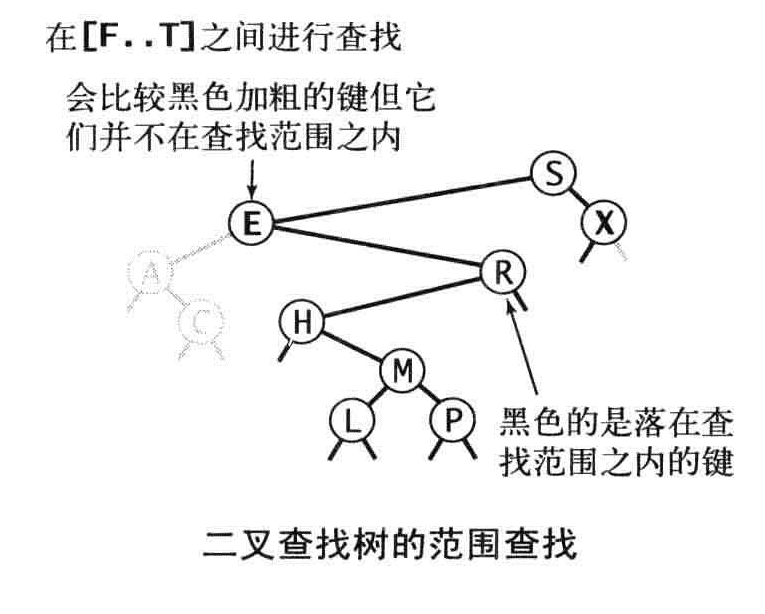
主要就是更新结点指向
命题E:在一颗二叉查找树中,所有操作的最坏情况下所需的事件都和树 的高度成正比。
/// <summary>
/// Get,Add,Delete等都使用递归
/// </summary>
/// <typeparam name="TKey"></typeparam>
/// <typeparam name="TValue"></typeparam>
public class BSTNet<TKey, TValue> : IBSTSearchDict<TKey, TValue> where TKey : IComparable
{
private class Node
{
public TKey Key { set; get; }
public TValue Value { set; get; }
public Node Left { set; get; }
public Node Right { set; get; }
/// <summary>
/// 每个结点计数器,每个结点下拥有结点的数量,包含自己
/// </summary>
public int Length { set; get; }
public Node(TKey key,TValue value,int length)
{
this.Key = key;
this.Value = value;
this.Length = length;
}
}
public BSTNet()
{
_root = null;
}
private Node _root;
public TValue this[TKey key] { get => Get(key); set => Add(key,value); }
public bool IsEmpty => length()==0;
public int Length => length();
private int length()
{
return length(_root);
}
private int length(Node node)
{
if (node == null) return 0;
else return node.Length;
}
private int length(TKey lo, TKey hi)
{
if (lo == default) throw new ArgumentException("this low key is default");
if (hi == default) throw new ArgumentException("this high is default");
if (lo.CompareTo(hi) > 0) return 0;
if (Contains(hi))
return Rank(hi) - Rank(lo) + 1;
else
return Rank(hi) - Rank(lo);
}
public int Rank(TKey key)
{
if (key == default) throw new ArgumentException("this key is default");
return rank(key, _root);
}
private int rank(TKey key, Node node)
{
if (node == null) return 0;
int cmp = key.CompareTo(node.Key);
if (cmp < 0) return rank(key, node.Left);
else if (cmp > 0) return 1 + length(node.Left) + rank(key, node.Right);
else return length(node.Left);
}
public bool Contains(TKey key)
{
if (key == default) throw new ArgumentException("this key is default value");
return Get(key) != default;
}
public TValue Get(TKey key)
{
return get(_root, key);
}
private TValue get(Node node,TKey key)
{
if (key == default || node == null) return default;
int cmp = key.CompareTo(node.Key);
if (cmp < 0) return get(node.Left, key);
if (cmp > 0) return get(node.Right, key);
return node.Value;
}
public void Add(TKey key, TValue value)
{
if (key == default) throw new ArgumentException("this key is default value");
if (value == default)
{
Delete(key);
return;
}
_root = add(_root,key,value);
}
/// <summary>
/// 使用了递归,所有查询的结点计数器都+1;
/// </summary>
/// <param name="node"></param>
/// <param name="key"></param>
/// <param name="value"></param>
/// <returns></returns>
private Node add(Node node,TKey key,TValue value)
{
if (node == null) return new Node(key, value, 1);
int cmp = key.CompareTo(node.Key);
if (cmp < 0) node.Left = add(node.Left, key, value);//追加到结点左边
if (cmp > 0) node.Right = add(node.Right, key, value);//追加到结点右边
else node.Value = value;
node.Length = 1 + length(node.Left) + length(node.Right);//计数器自增
return node;
}
public TKey Ceiling(TKey key)
{
if (key == default || IsEmpty) return default;
Node tem = ceiling(_root, key);
if (tem == null) throw new ArgumentException("this key is too large");
else return tem.Key;
}
private Node ceiling(Node node,TKey key)
{
if (node == null) return null;
int cmp = key.CompareTo(node.Key);
if (cmp == 0) return node;
if(cmp<0)
{
Node tem = ceiling(node.Left, key);
if (tem != null) return tem;
else return node;
}
return ceiling(node.Right, key);
}
public void Delete(TKey key)
{
if (key == default) return;
_root = delete(_root, key);
}
private Node delete(Node node,TKey key)
{
if (node == null || key == default) return default;
int cmp = key.CompareTo(node.Key);
if (cmp < 0) node.Left = delete(node.Left, key);
else if (cmp > 0) node.Right = delete(node.Right, key);
else
{
//该结点就是删除的结点
if (node.Right == null) return node.Left;
else if (node.Left == null) return node.Right;
else
{
Node tem = node;//左右都正常
node = min(tem.Right);//将右边
node.Right = deleteMin(tem.Right);
node.Left = tem.Left;
}
}
node.Length = 1 + length(node.Left) + length(node.Right);
return node;
}
public void DeleteMax()
{
if (IsEmpty) return;
_root = deleteMax(_root);
}
private Node deleteMax(Node node)
{
if (node == null) return null;
if (node.Right == null) return node.Left;
node.Right = deleteMax(node.Right);
node.Length = length(node.Left) + length(node.Right) + 1;
return node;
}
public void DeleteMin()
{
if (IsEmpty) return;
_root = deleteMin(_root);
}
private Node deleteMin(Node node)
{
if (node == null) return null;
if (node.Left == null) return node.Right;
node.Left = deleteMin(node.Left);
node.Length = 1 + length(node.Left) + length(node.Right);
return node;
}
public void Dispose()
{
Dispose(true);
}
protected virtual void Dispose(bool disposing)
{
if(disposing)
{
if (!IsEmpty)
DeleteMin();
}
}
public TKey Floor(TKey key)
{
if (key == default || IsEmpty) return default;
Node tem = floor(_root, key);
if (tem == null) throw new ArgumentException("this key is too small");
else return tem.Key;
}
private Node floor(Node node,TKey key)
{
if (key == default) return null;
int cmp = key.CompareTo(node.Key);
if (cmp == 0) return node;
if (cmp < 0) return floor(node.Left, key);
Node tem = floor(node.Right, key);
if (tem != null) return tem;
else return node;
}
public TKey Floor2(TKey key)
{
TKey tem = floor2(_root, key, default);
if (tem == null) throw new ArgumentException("argument to floor() is too small");
else return tem;
}
private TKey floor2(Node node, TKey key, TKey best)
{
if (node == null) return best;
int cmp = key.CompareTo(node.Key);
if (cmp < 0) return floor2(node.Left, key, best);
else if (cmp > 0) return floor2(node.Right, key, node.Key);
else return node.Key;
}
public TKey Max()
{
if (IsEmpty) return default;
return max(_root).Key;
}
private Node max(Node node)
{
if (node == null) return null;
if (node.Right == null) return node;
else return max(node.Right);
}
public TKey Min()
{
if (IsEmpty) return default;
return min(_root).Key;
}
private Node min(Node node)
{
if (node == null) return null;
if (node.Left == null) return node;
else return min(node.Left);
}
}
平衡查找树(2-3查找树)
二叉查找树最坏的情况还是很糟糕的,平衡查找树可以有效解决这个问题,无论数组的初始状态如何,它的运行时间都是对数级别的。
定义:一颗2-3查找树由以下结点组成:
- 2-结点,含有一个键和两条链接,左链接指向的2-3树中的键都小于该结点,右链接指向的2-3树种的键都大于该结点。
- 3-结点,含有两个键(及其对应的值)和三条链接,左链接指向的2-3树中的键都小于该结点,中链接指向的2-3树种的键都位于该结点的两个键之间。右链接指向的2-3树的键都大于该结点。
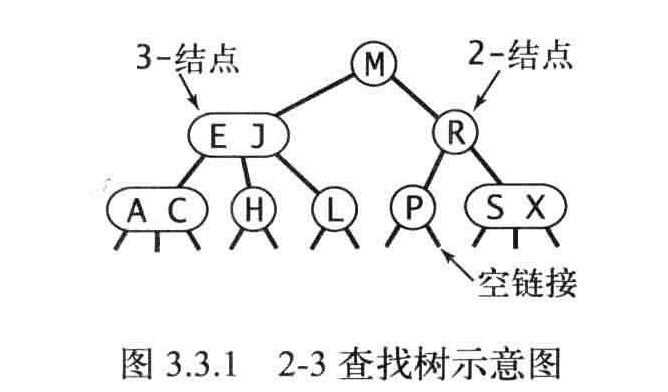
一颗完美平衡的2-3查找树种的所有空连接到根结点的距离都应该是相同的。
查找
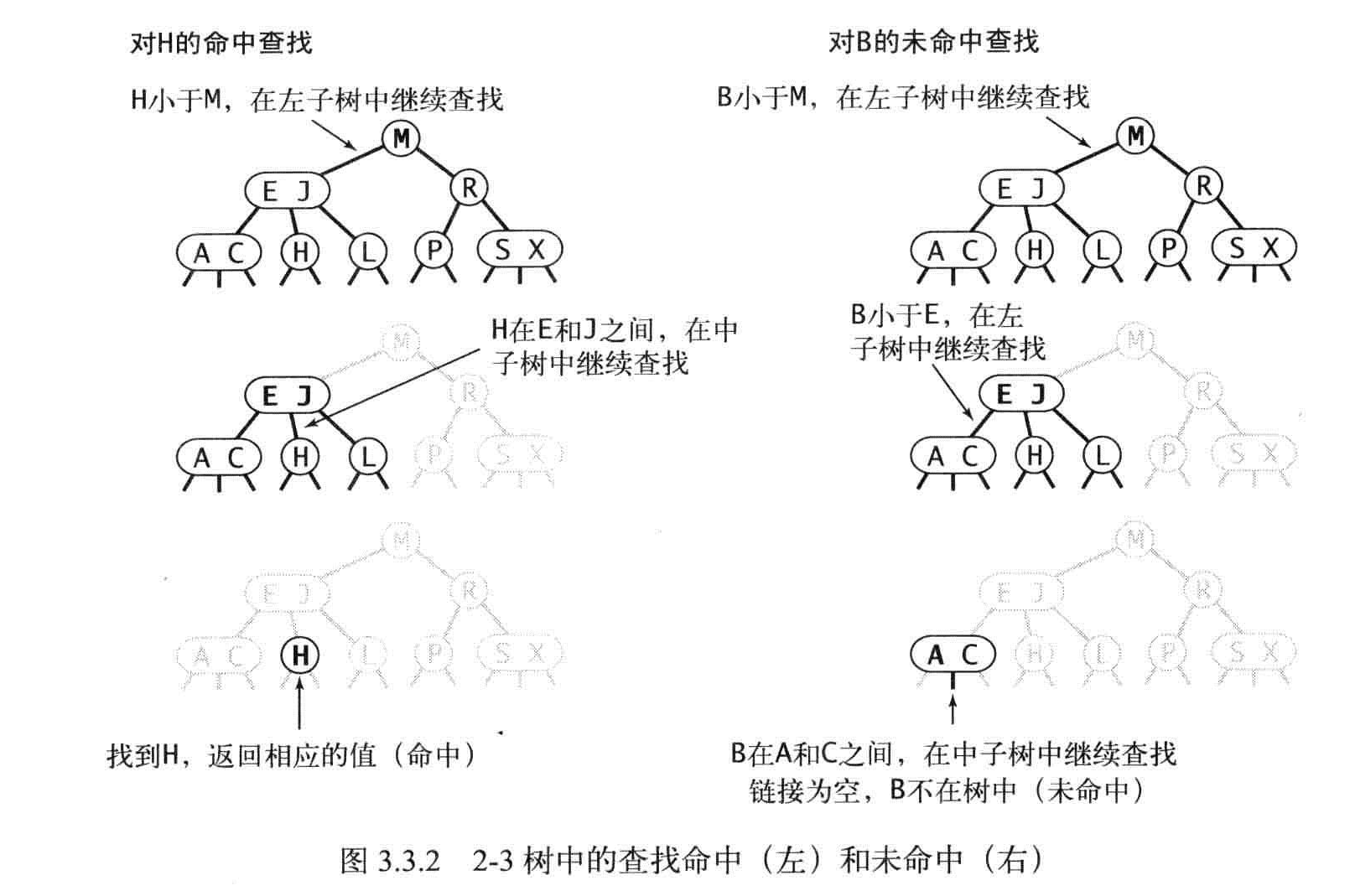
插入
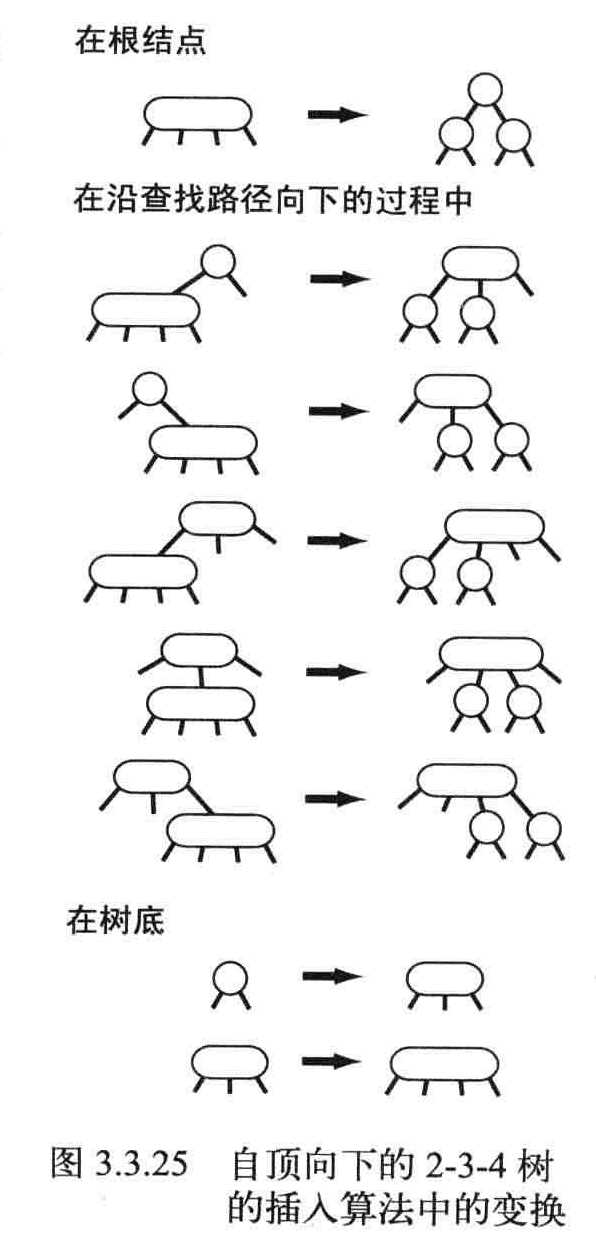
先进行一次未命中的查找,然后把新结点挂在树的底部,如果未命中的查找结束于一个2-结点,就将2-结点换成3-结点。如果未命中的查找结束于一个3-结点,就先将3-结点换成4-结点,然后转换成2-3树。
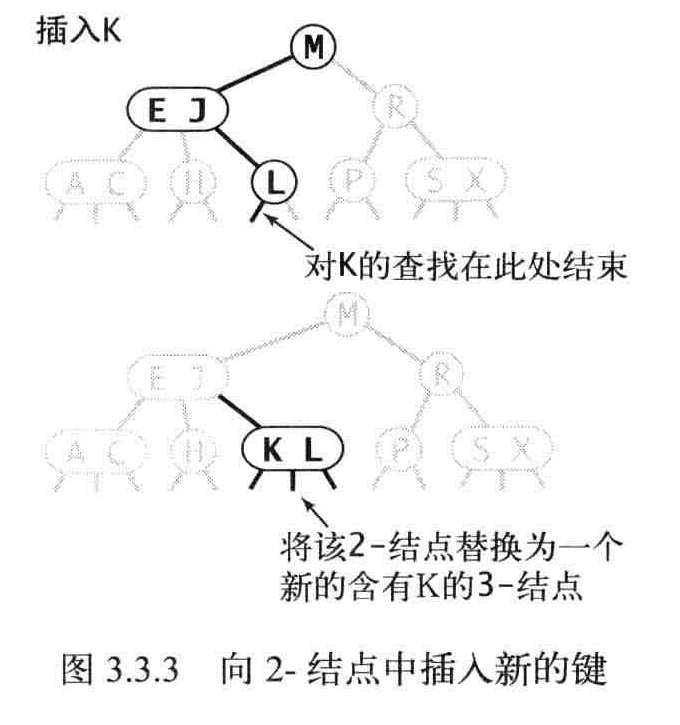
4结点转换成2-3树要麻烦,如果4-结点的父结点是2-结点,那么4-结点就转换成一个3-结点和2个2-结点。
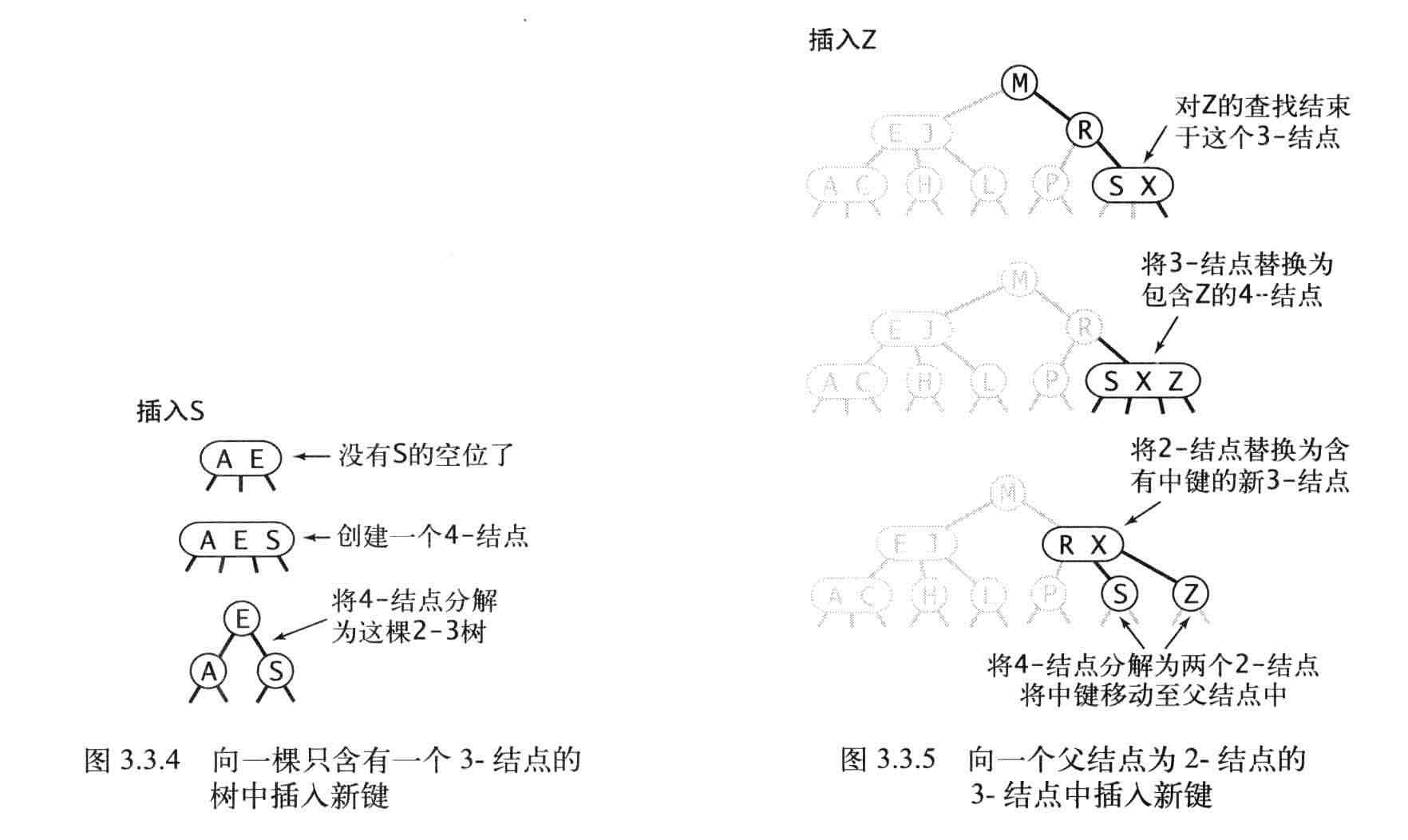
如果4-结点的父结点是2-结点,爷结点也是2-结点,那么就一次向上转换,直到根结点,然后树的根高就会加一。
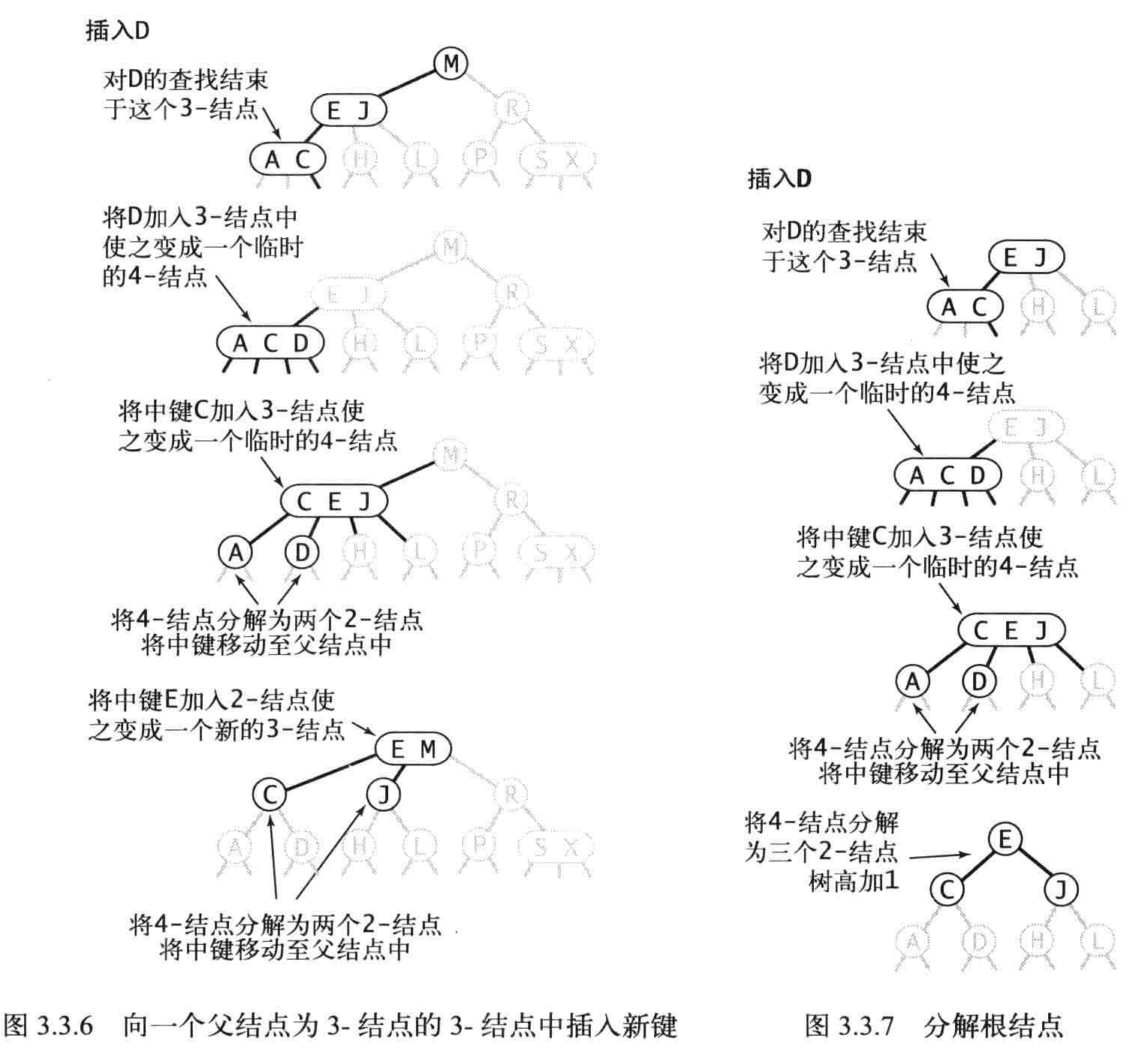
分解4-结点一共有6种情况
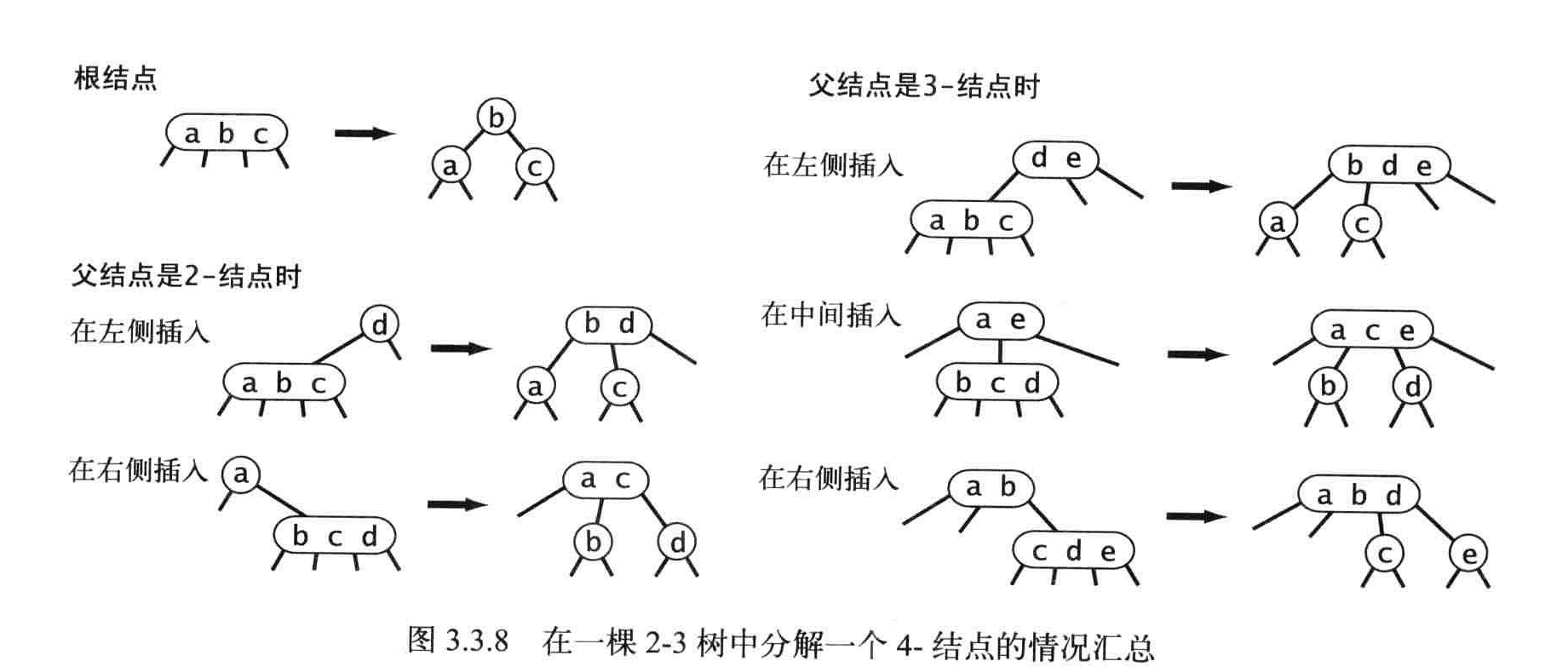
4结点的分解不会影响树的有序性和平衡性
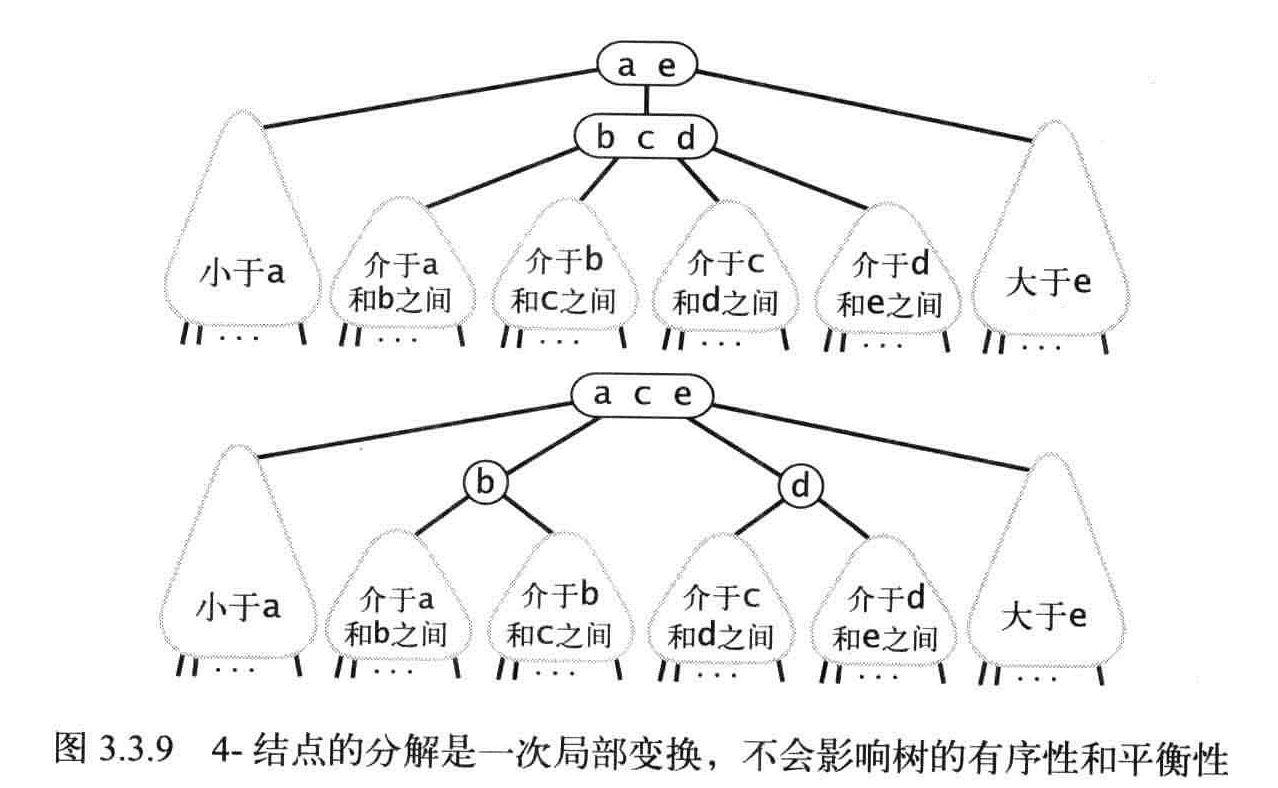
命题F:在一棵大小为N的2-3树中,查找和插入操作访问的结点必然不超过lgN个。
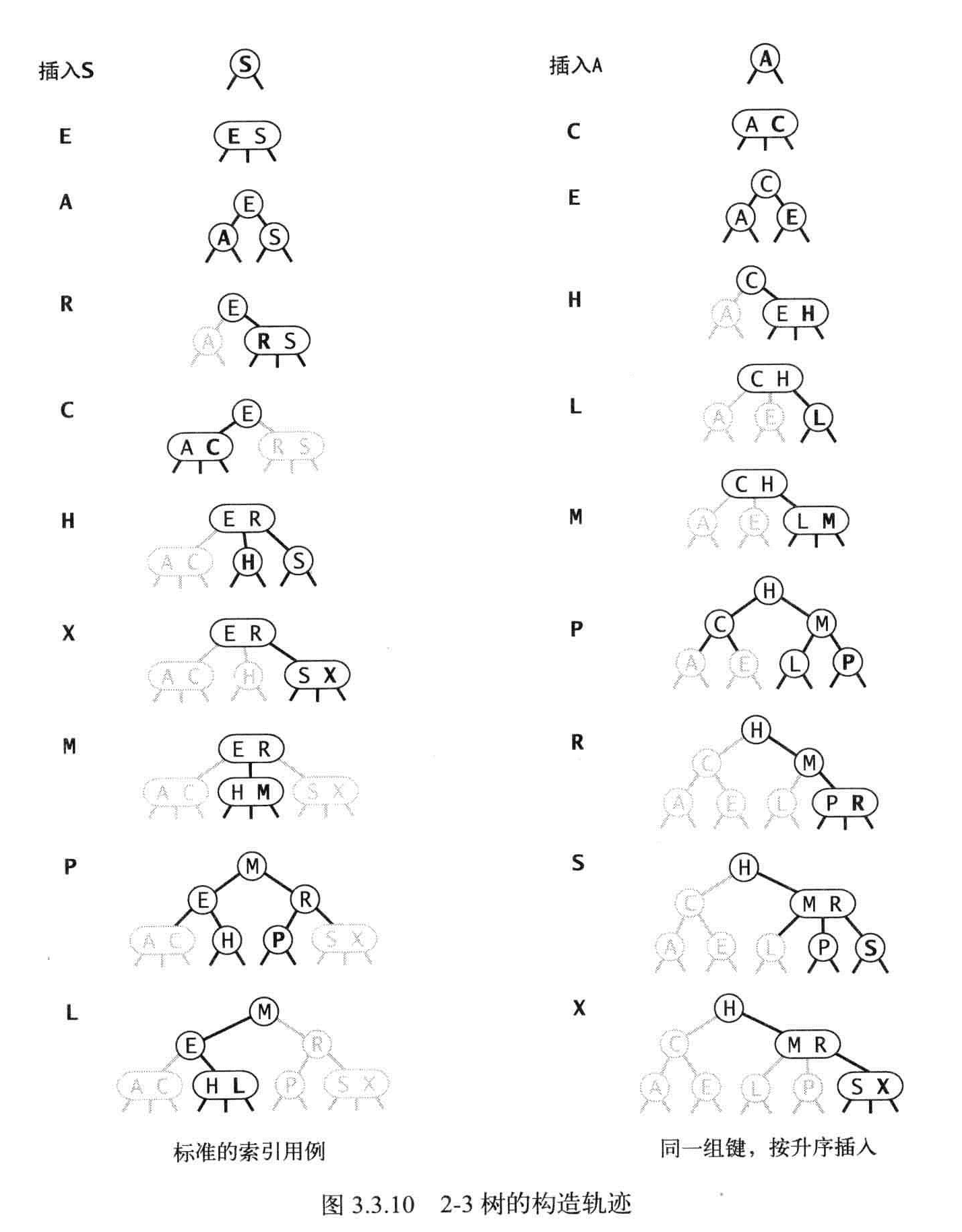
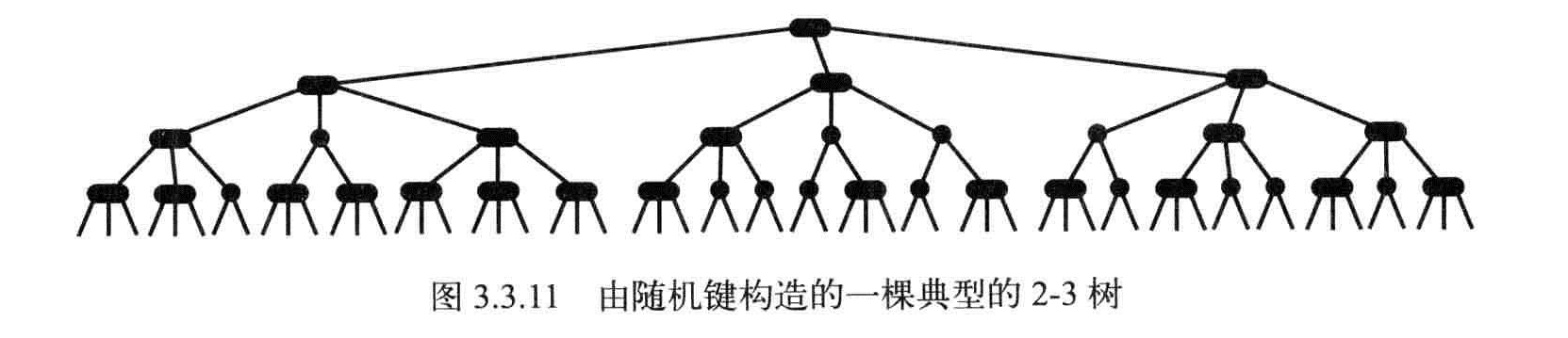
含有10亿个结点的一颗2-3树的高度仅在19-30之间,最后访问30个结点就能够在10亿个键中进行任意插入和查找。
红黑二叉查找树(红黑树)
通过红链接将2-3查找树的3-结点变成两个2结点的链接。
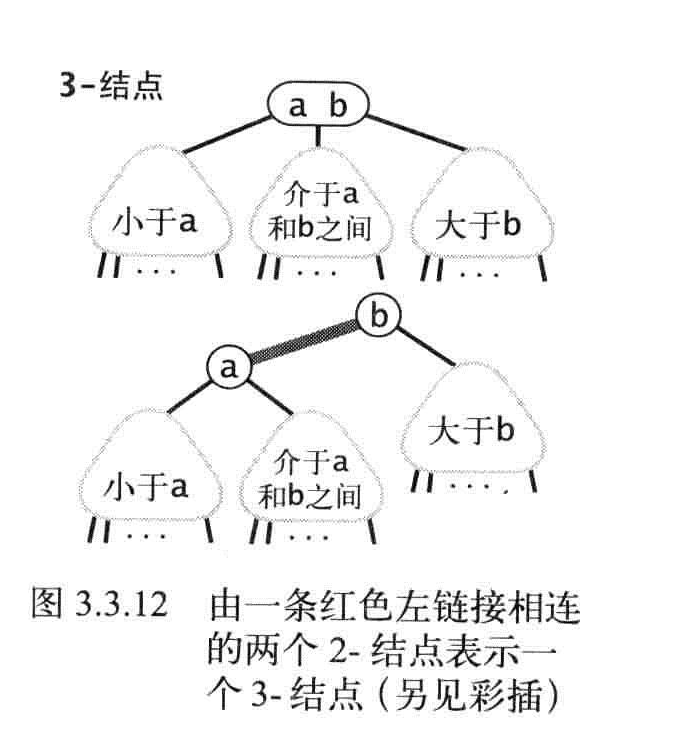
红黑树的定义:
- 红链接均为左链接
- 没有任何一个结点同时和两条红链接相连。
- 该树是一个完美黑色平衡树,任意空连接到根结点的路径上的黑链接数量相同。
如果将红链接画平
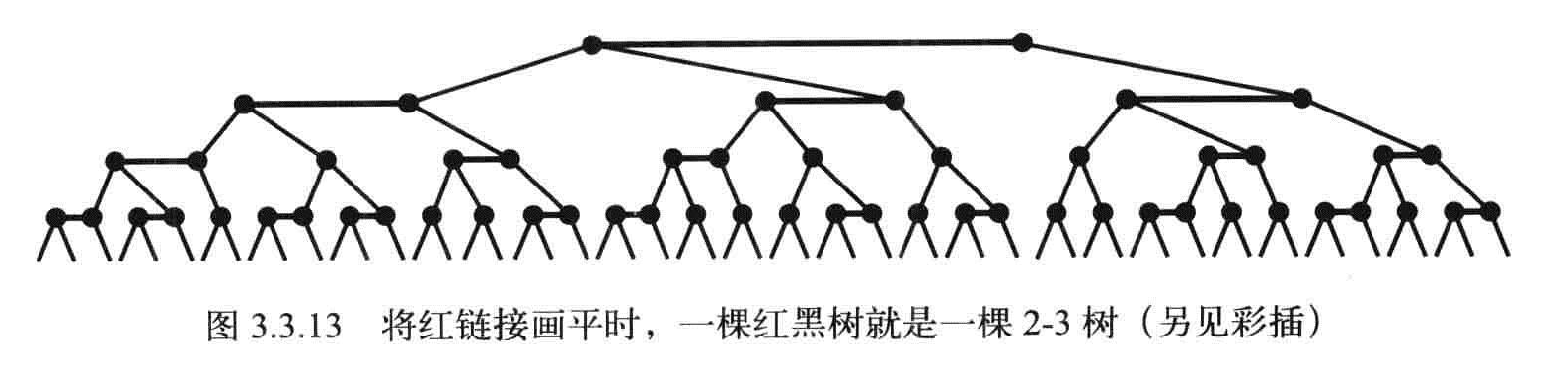
结点中通过一个属性Color来判定指向该结点是红色还是黑色。同时约定空连接为黑色

旋转
左旋转:右链接转化为左链接
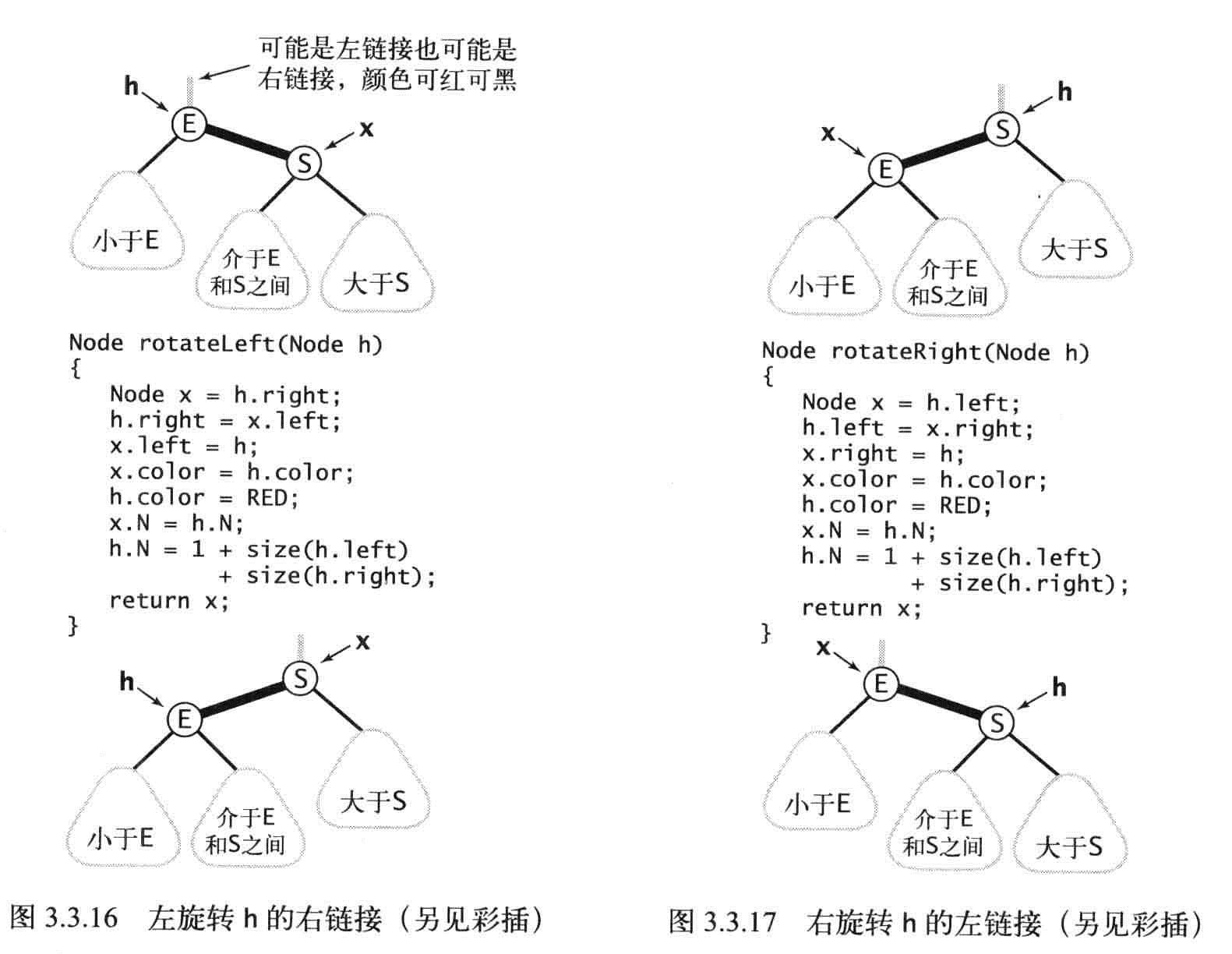
2-结点插入
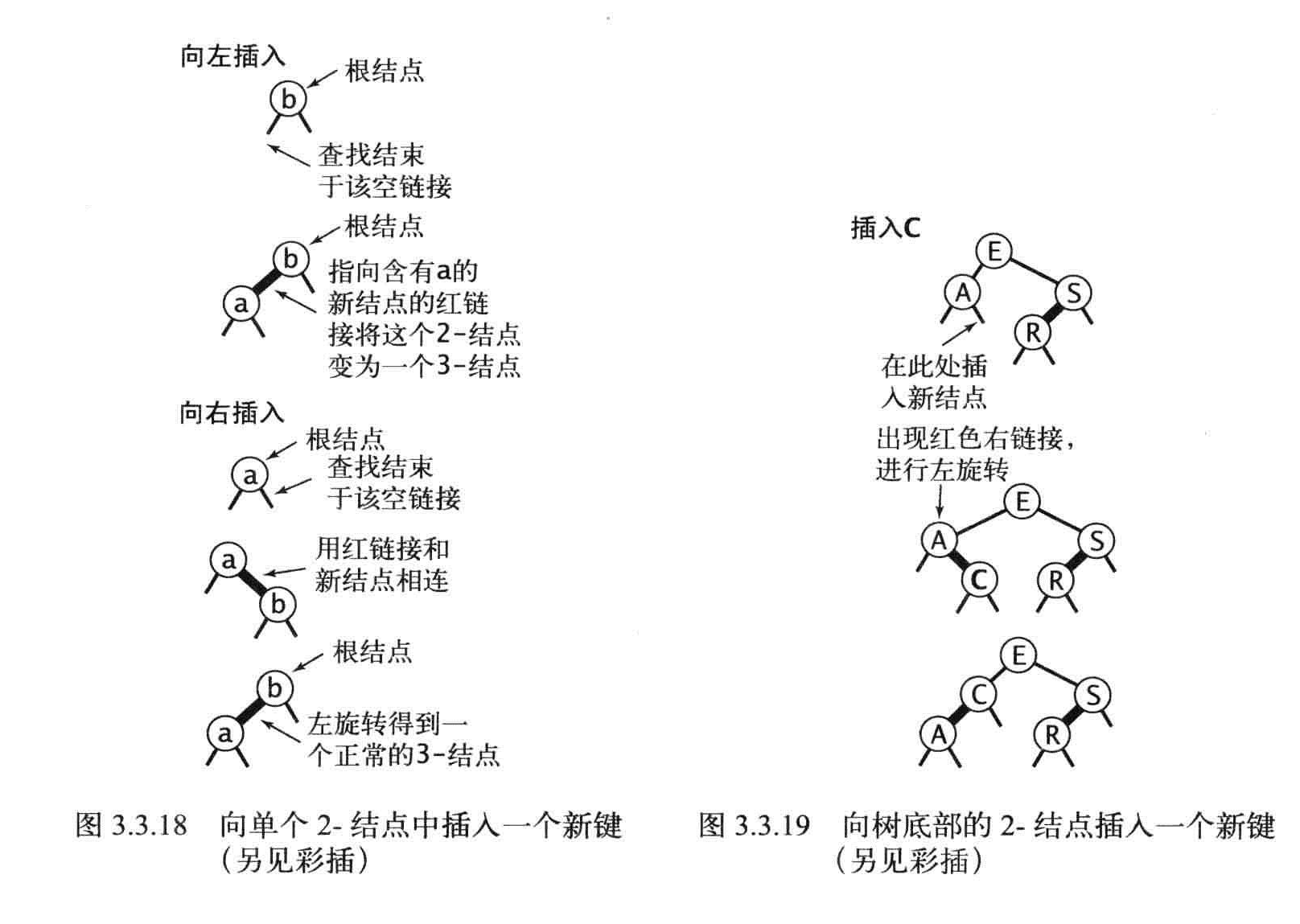
3-结点插入
有三种情况,通过0次,1次,2次旋转以及颜色的变化得到期望的结果。
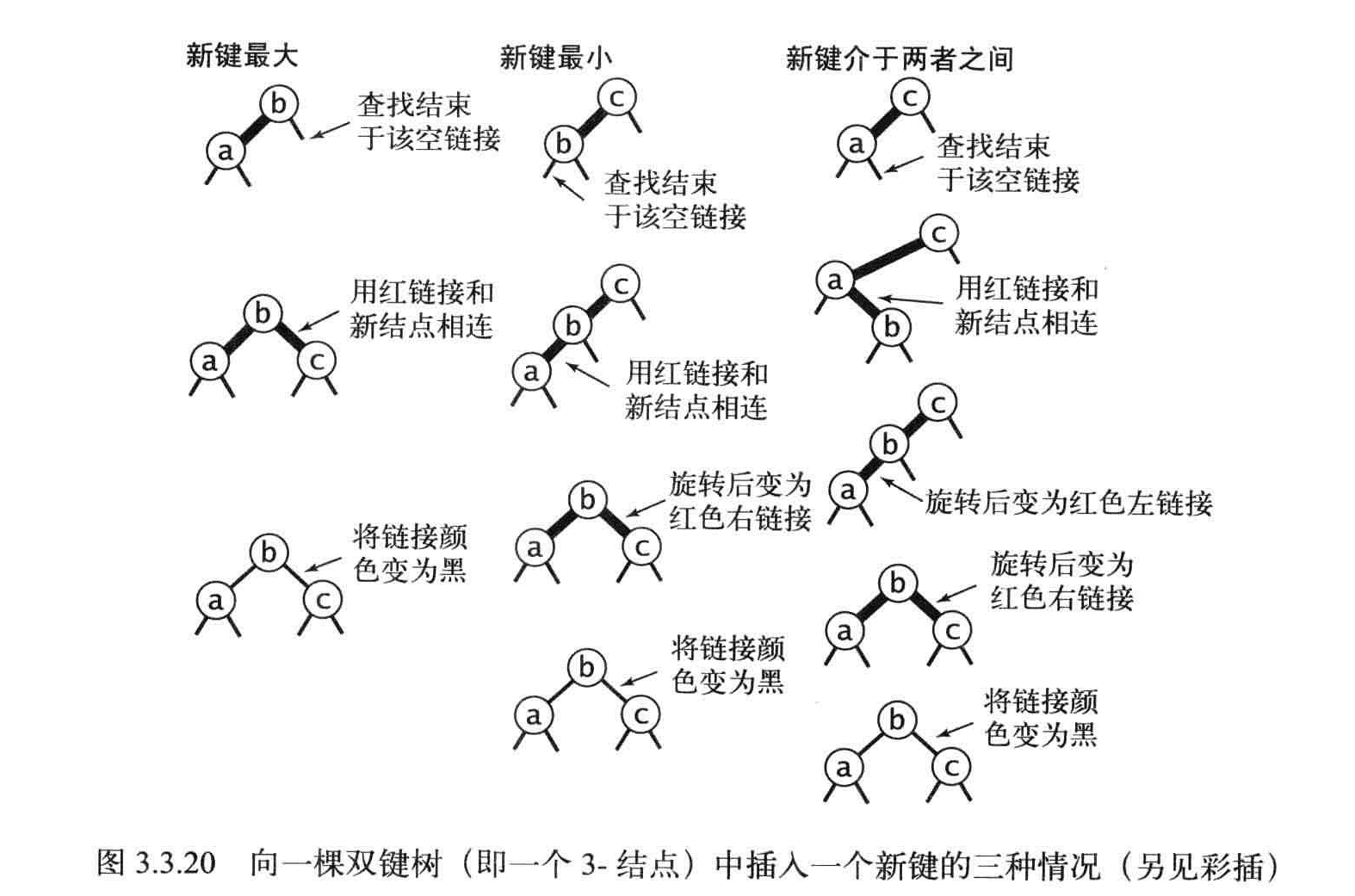
颜色变化

底部插入
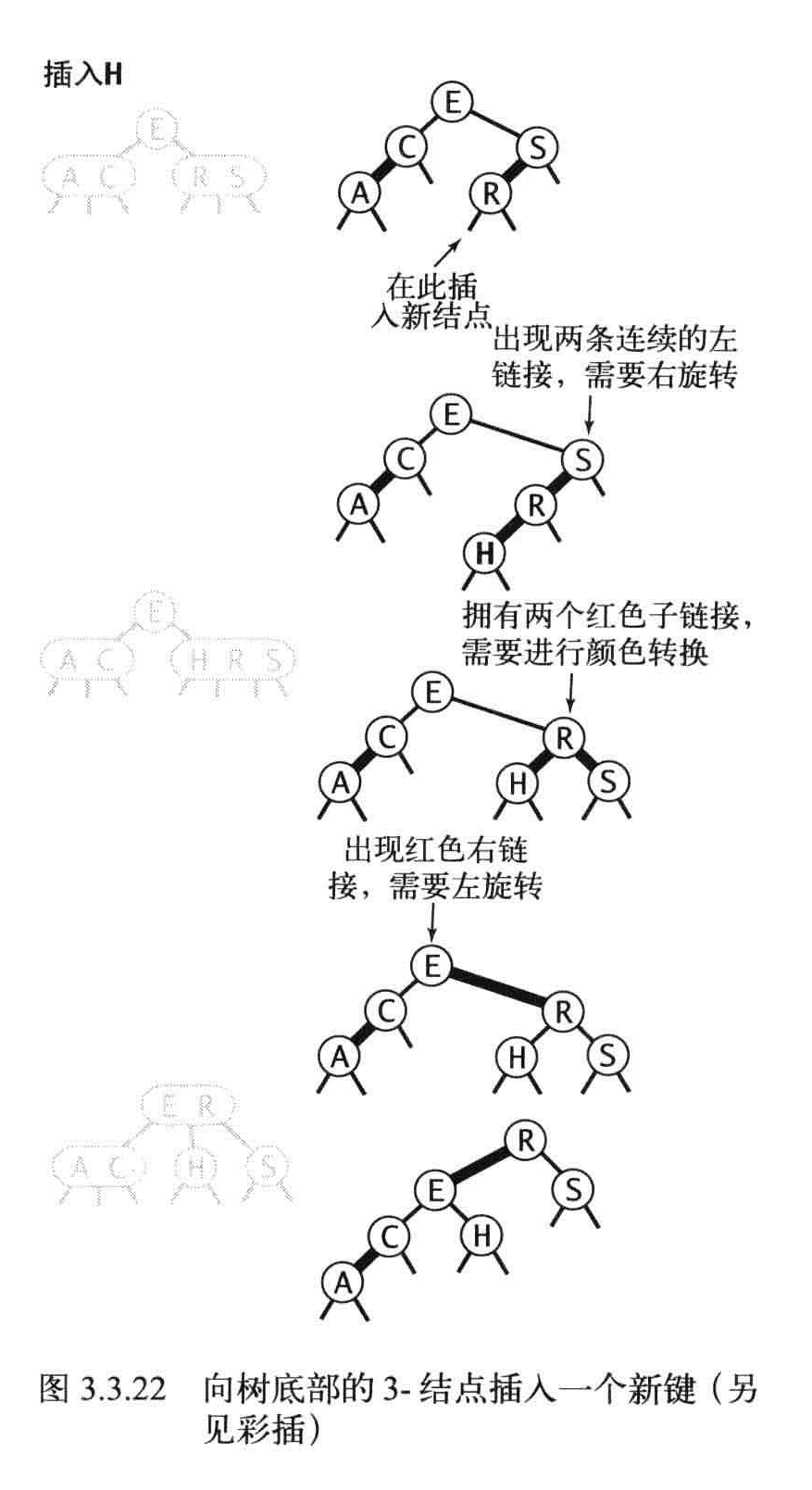
插入总结
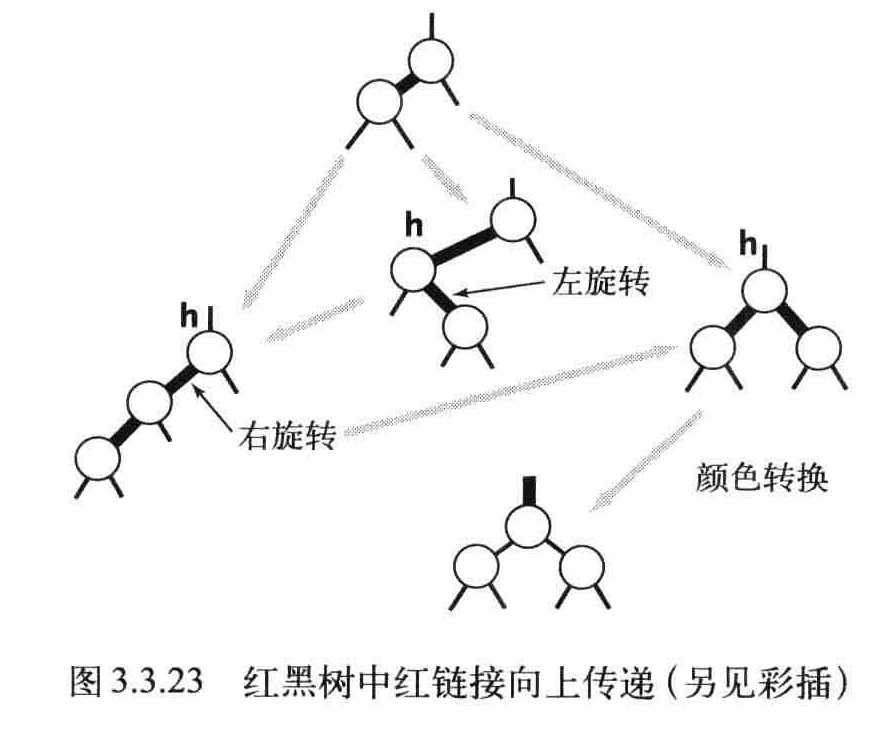
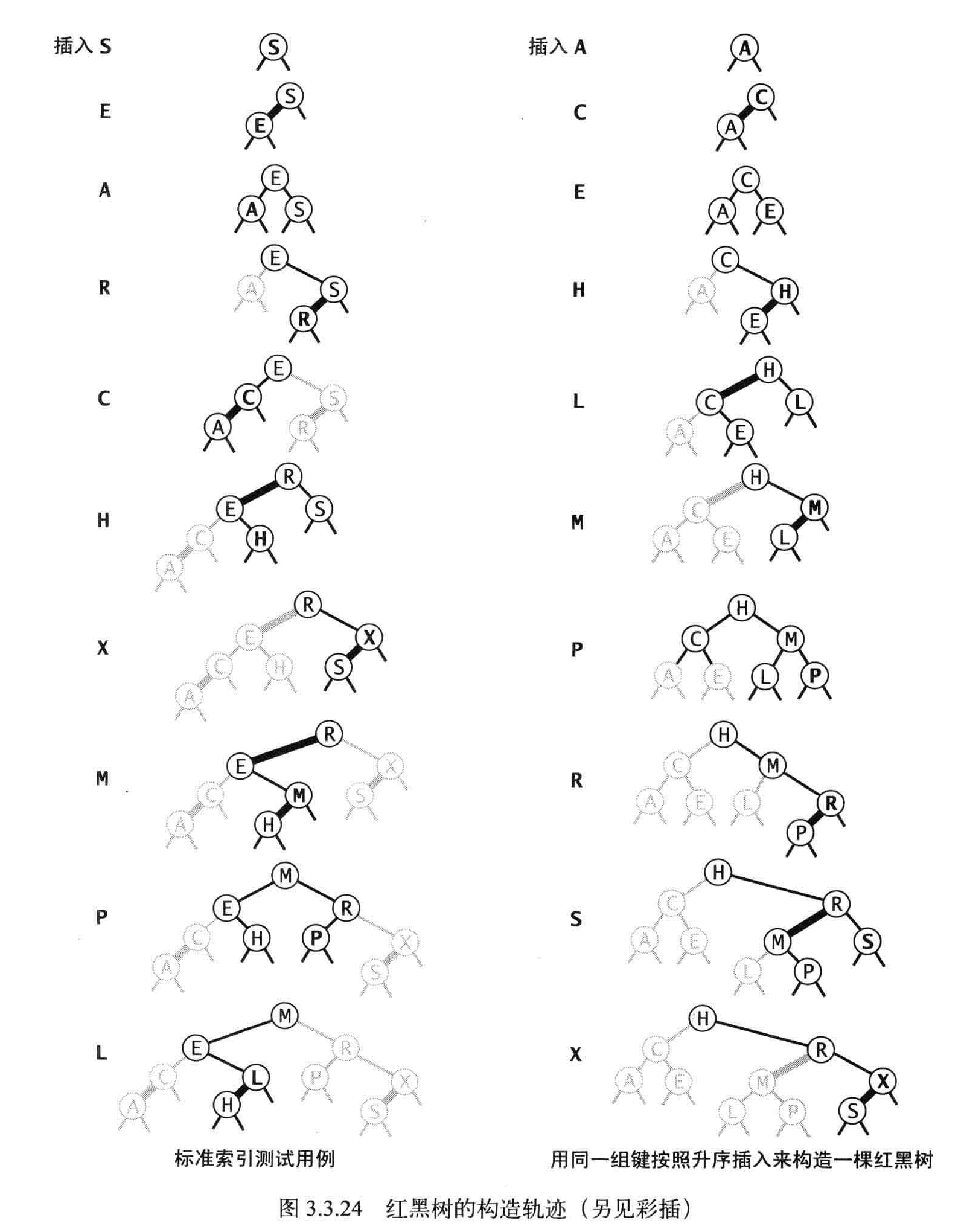
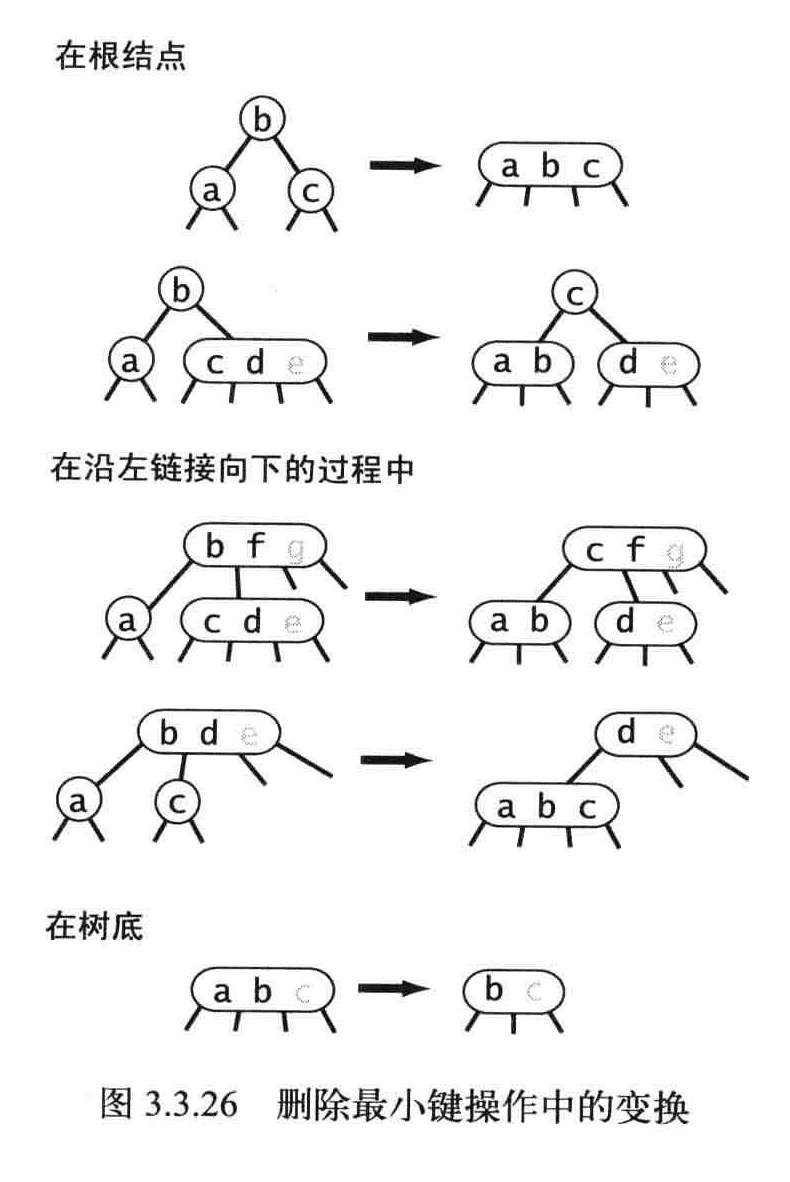
删除最小键
如果查找的键在最底部,可以直接删除它。
如果不在最底部,就需要和后继结点交换。问题就可以转换成在一棵根结点不是2-结点的子树中删除最小的键。
命题G:一棵大小为N的红黑树的高度不会超过2lgN
命题H:一棵大小为N的红黑树中,根结点到任意结点的平均路径长度为~1.00LgN。
命题I:在一棵红黑树中,以下操作在最坏情况下所需的时间是对数级别:查找,插入,查找最小键,查找最大键,floor,ceiling,rank,select(),删除最小键,删除最大键,删除,范围查询。
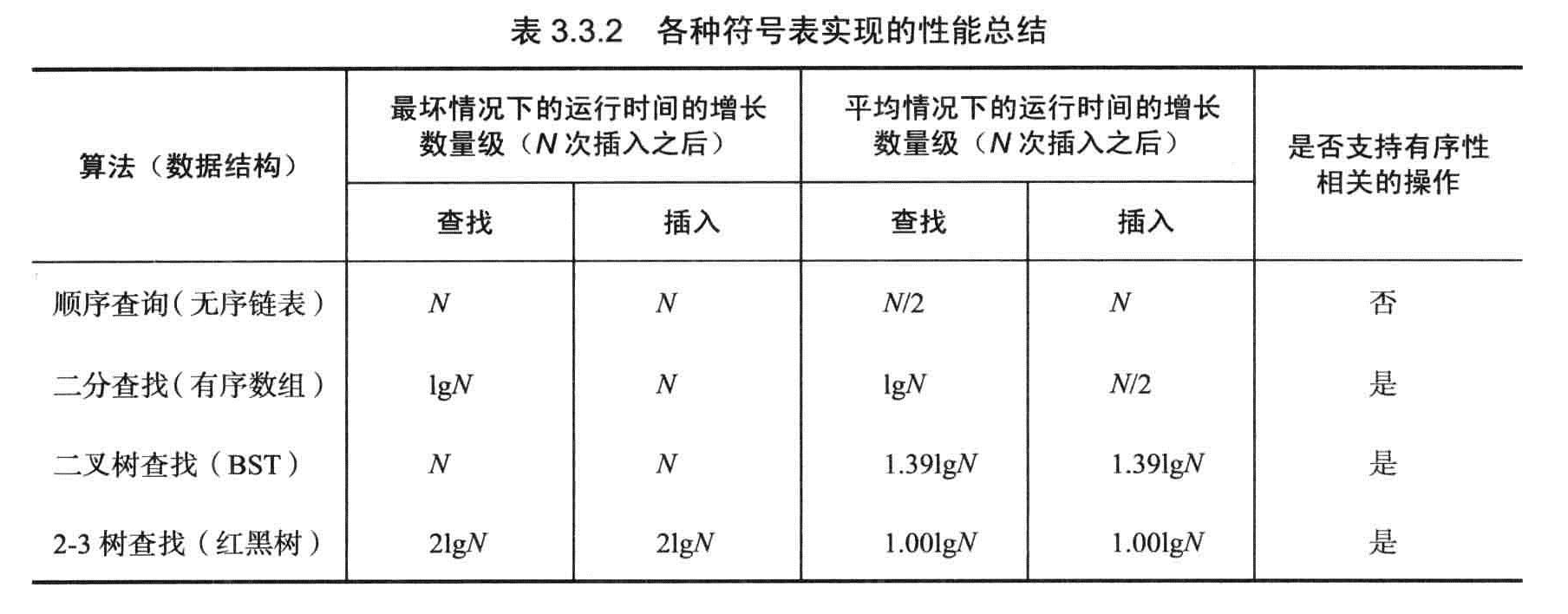
千亿的数据量十几次比较就可以找到。
public class RedBlackBSTNet<TKey, TValue> : IRedBlackBST<TKey, TValue> where TKey : IComparable<TKey>
{
private static readonly bool RED = true;
private static readonly bool BLACK = false;
private Node _root;
private class Node
{
public TKey Key { set; get; }
public TValue Value { set; get; }
public Node Right { set; get; }
public Node Left { set; get; }
/// <summary>
/// 指向该结点的颜色
/// </summary>
public bool Color { set; get; }
/// <summary>
/// 该结点下的结点量,包括本结点
/// </summary>
public int Length { set; get; }
public Node(TKey key,TValue value,bool color,int length)
{
this.Key = key;
this.Value = value;
this.Color = color;
this.Length = length;
}
}
public RedBlackBSTNet()
{
}
/// <summary>
/// 默认空结点是黑色
/// </summary>
/// <param name="node"></param>
/// <returns></returns>
private bool isRed(Node node)
{
if (node == null) return false;
return node.Color == RED;
}
private int length(Node node)
{
if (node == null) return 0;
return node.Length;
}
private int length()
{
return length(_root);
}
public TValue this[TKey key] { get =>Get(key); set => Add(key,value); }
public bool IsEmpty => _root==null;
public int Length => length();
public void Add(TKey key, TValue value)
{
if (key == default) return;
if (value == default)
{
Delete(key);
return;
}
_root = add(_root, key, value);
_root.Color = BLACK;
}
/// <summary>
/// 这边在递归的上一层修改了颜色
/// </summary>
/// <param name="node"></param>
/// <param name="key"></param>
/// <param name="value"></param>
/// <returns></returns>
private Node add(Node node,TKey key,TValue value)
{
if (node == null) return new Node(key, value, RED, 1);//新增结点都是3-结点
int cmp = key.CompareTo(node.Key);
if (cmp < 0) node.Left = add(node.Left, key, value);
else if (cmp > 0) node.Right = add(node.Right, key, value);
else node.Value = value;
//修改颜色,让所有的红色结点都是左节点,直接看插入总结
if (isRed(node.Right) && !isRed(node.Left)) node = rotateLeft(node);//右边是红色,左边不是红色
if (isRed(node.Left) && isRed(node.Left.Left)) node = rotateRight(node);//如果左边是红色,左边的左边也是红色
if (isRed(node.Left) && isRed(node.Right)) flipColors(node);//如果左右连边都是红色
node.Length = length(node.Left) + length(node.Right) + 1;
return node;
}
/// <summary>
/// 翻转颜色,三个结点颜色全部反转
/// </summary>
/// <param name="node"></param>
private void flipColors(Node node)
{
//node must have opposite color of its two children
node.Color = !node.Color;
node.Left.Color = !node.Left.Color;
node.Right.Color = !node.Right.Color;
}
/// <summary>
/// 红左链接变成红右连接,node->h,tem->x
/// </summary>
/// <param name="node"></param>
/// <returns></returns>
private Node rotateRight(Node h)
{
Node x = h.Left;
h.Left = x.Right;
x.Right = h;
x.Color = x.Right.Color;
x.Right.Color = RED;
x.Length = h.Length;
h.Length = length(h.Left) + length(h.Right) + 1;
return x;
}
/// <summary>
/// 红右连接变成左连接
/// </summary>
/// <param name="h"></param>
/// <returns></returns>
private Node rotateLeft(Node h)
{
Node x = h.Right;
h.Right = x.Left;
x.Left = h;
x.Color = x.Left.Color;
x.Left.Color = RED;
x.Length = h.Length;
h.Length = length(h.Left) + length(h.Right) + 1;
return x;
}
public TKey Ceiling(TKey key)
{
if (key == default || IsEmpty) return default;
Node node = ceiling(_root, key);
if (node == null) throw new ArgumentException("this key is too small");
else return node.Key;
}
private Node ceiling(Node node,TKey key)
{
if (node == null) return null;
int cmp = key.CompareTo(node.Key);
if (cmp == 0) return node;
if(cmp>0) return ceiling(node.Right, key);
Node tem = ceiling(node.Left, key);
if (tem != null) return tem;
else return node;
}
public bool Contains(TKey key)
{
return Get(key) != default;
}
public void Delete(TKey key)
{
throw new NotImplementedException();
}
private Node delete(Node node,TKey key)
{
if (key.CompareTo(node.Key) < 0)
{
if (!isRed(node.Left) && !isRed(node.Left.Left))
node = moveRedLeft(node);
node.Left = delete(node.Left, key);
}
else
{
if (isRed(node.Left))
node = rotateRight(node);
if (key.CompareTo(node.Key) == 0 && (node.Right == null))
return null;
if (!isRed(node.Right) && !isRed(node.Right.Left))
node = moveRedRight(node);
if (key.CompareTo(node.Key) == 0)
{
Node x = min(node.Right);
node.Key = x.Key;
node.Value = x.Value;
// h.val = get(h.right, min(h.right).key);
// h.key = min(h.right).key;
node.Right = deleteMin(node.Right);
}
else node.Right = delete(node.Right, key);
}
return balance(node);
}
public void DeleteMax()
{
if (IsEmpty)
return;
if (!isRed(_root.Left) && !isRed(_root.Right))
_root.Color = RED;
_root = deleteMax(_root);
if (!IsEmpty) _root.Color = BLACK;
}
private Node deleteMax(Node node)
{
if (isRed(node.Left))
node = rotateRight(node);
if (node.Right == null)
return null;
if (!isRed(node.Right) && !isRed(node.Right.Left))
node = moveRedRight(node);
node.Right = deleteMax(node.Right);
return balance(node);
}
public void DeleteMin()
{
if (IsEmpty) return;
if (!isRed(_root.Left) && !isRed(_root.Right))
_root.Color = RED;
_root = deleteMin(_root);
if (!IsEmpty) _root.Color = BLACK;
}
/// <summary>
/// 递归用的好
/// </summary>
/// <param name="node"></param>
/// <returns></returns>
private Node deleteMin(Node node)
{
if (node.Left == null)
return null;
if (!isRed(node.Left) && !isRed(node.Left.Left))
node = moveRedLeft(node);
node.Left = deleteMin(node.Left);
return balance(node);
}
/// <summary>
/// 恢复红黑树的状态
/// </summary>
/// <param name="h"></param>
/// <returns></returns>
private Node balance(Node node)
{
if (isRed(node.Right)) node = rotateLeft(node);
if (isRed(node.Left) && isRed(node.Left.Left)) node = rotateLeft(node);
if (isRed(node.Left) && isRed(node.Right)) flipColors(node);
node.Length = length(node.Left) + length(node.Right) + 1;
return node;
}
/// <summary>
///
/// </summary>
/// <param name="node"></param>
/// <returns></returns>
private Node moveRedLeft(Node node)
{
flipColors(node);
if(isRed(node.Right.Left))
{
node.Right = rotateRight(node.Right);
node = rotateLeft(node);
flipColors(node);
}
return node;
}
private Node moveRedRight(Node node)
{
flipColors(node);
if(isRed(node.Left.Left))
{
node = rotateRight(node);
flipColors(node);
}
return node;
}
public void Dispose()
{
Dispose(true);
}
protected virtual void Dispose(bool disposing)
{
if(disposing)
{
if(!IsEmpty)
{
DeleteMin();
}
}
}
public TKey Select(int rank)
{
if (rank < 0 || rank > length())
return default;
return select(_root, rank);
}
private TKey select(Node node, int rank)
{
if (node == null) return default;
int leftlength = length(node.Left);
if (leftlength > rank) return select(node.Left, rank);
else if (leftlength < rank) return select(node.Right, rank - leftlength - 1);
else return node.Key;
}
public TKey Floor(TKey key)
{
if (key == default || IsEmpty)
return default;
Node node = floor(_root, key);
if (node == null) throw new ArgumentException("this key is too small");
else return node.Key;
}
private Node floor(Node node,TKey key)
{
if (node == null) return null;
int cmp = key.CompareTo(node.Key);
if (cmp == 0) return node;
if (cmp < 0) return floor(node.Left, key);
Node tem = floor(node.Right, key);
if (tem != null) return tem;
else return node;
}
public TValue Get(TKey key)
{
if (key == default || IsEmpty)
return default;
return get(_root, key);
}
private TValue get(Node node,TKey key)
{
while(node !=null)
{
int cmp = key.CompareTo(node.Key);
if (cmp < 0) node = node.Left;
else if (cmp > 0) node = node.Right;
else return node.Value;
}
return default;
}
public int Height()
{
return height(_root);
}
private int height(Node node)
{
if (node == null) return -1;
return 1 + Math.Max(height(node.Left), height(node.Right));
}
public TKey Max()
{
if (IsEmpty) return default;
return max(_root).Key;
}
private Node max(Node node)
{
if (node.Right == null) return node;
else return max(node.Right);
}
public TKey Min()
{
if (IsEmpty) return default;
return min(_root).Key;
}
private Node min(Node node)
{
if (node.Left == null) return node;
else return min(node.Left);
}
public int Rank(TKey key)
{
if (key == default) throw new ArgumentException("this key is default value");
return rank(key, _root);
}
private int rank(TKey key, Node node)
{
if (node == null) return 0;
int cmp = key.CompareTo(node.Key);
if (cmp < 0) return rank(key, node.Left);
else if (cmp > 0) return 1 + length(node.Left) + rank(key, node.Right);
else return length(node.Left);
}
}
散列表
如果所有的键都是小整数,可以用一个数组来实现无序的符号表,将键作为数组的索引而数组中键i处储存的就是它对应的值。用算术操作将键转化为数组的索引来访问数组中的键值对。
- 用散列函数将被查找的键转化为数组的一个索引。
- 处理碰撞和冲突过程,有两个方法:拉链法和线性探测法。
散列表是时间和空间上作出权衡的例子,如果没有内存限制,可以直接将键作为数组的索引,查找操作只需要访问内存一次就可以完成。
概率论是数学分析重大成果,使用散列标,可以实现在一般应用中有常数级别的查找和插入操作的符号表。
散列函数
- 将key转化为[0-M]内的整数。
- 转化的整数在[0-M-1]上是均匀分布的。
余留法
使用素数余留法
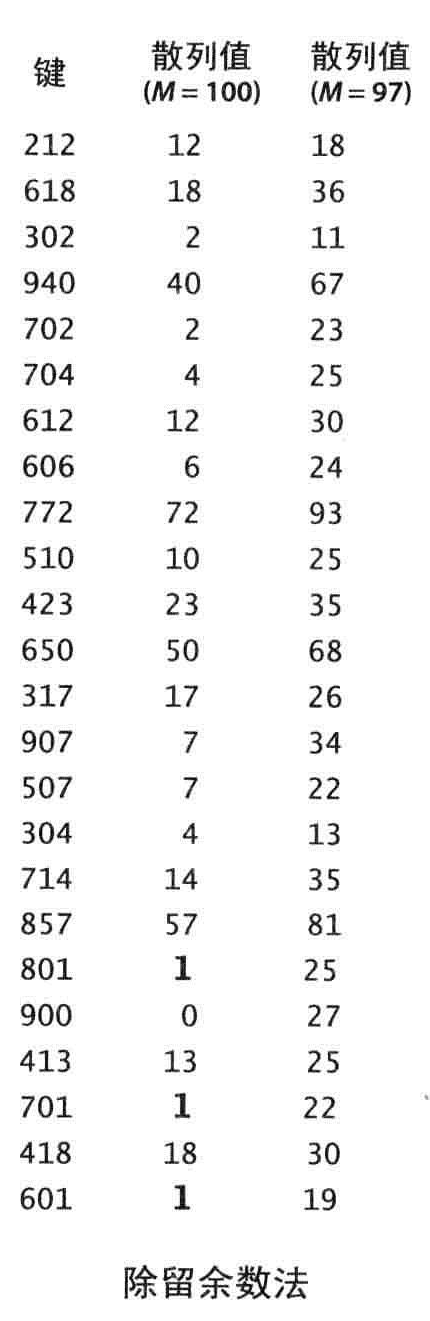
HashCode
将hashcode的返回值转化为数组的索引。通过hashcode和余留发结合起来产生0到M-1的整数。
private int hash(Key x)
{
return (x.hashCode() & 0x7fffffff) & M
}
软缓存
将每个键的散列值缓存起来,这样减少计算散列值的时间
一致性,高校性,均匀性
假设J:使用散列函数能够均匀并独立地将所有的键散布于0到M-1之间。
处理碰撞
拉链法
将M的数组中每个元素指向一个链表。链表中每个结点都存储了散列值为该元素的索引键值对。
需要M足够大,这样链表就比较小。
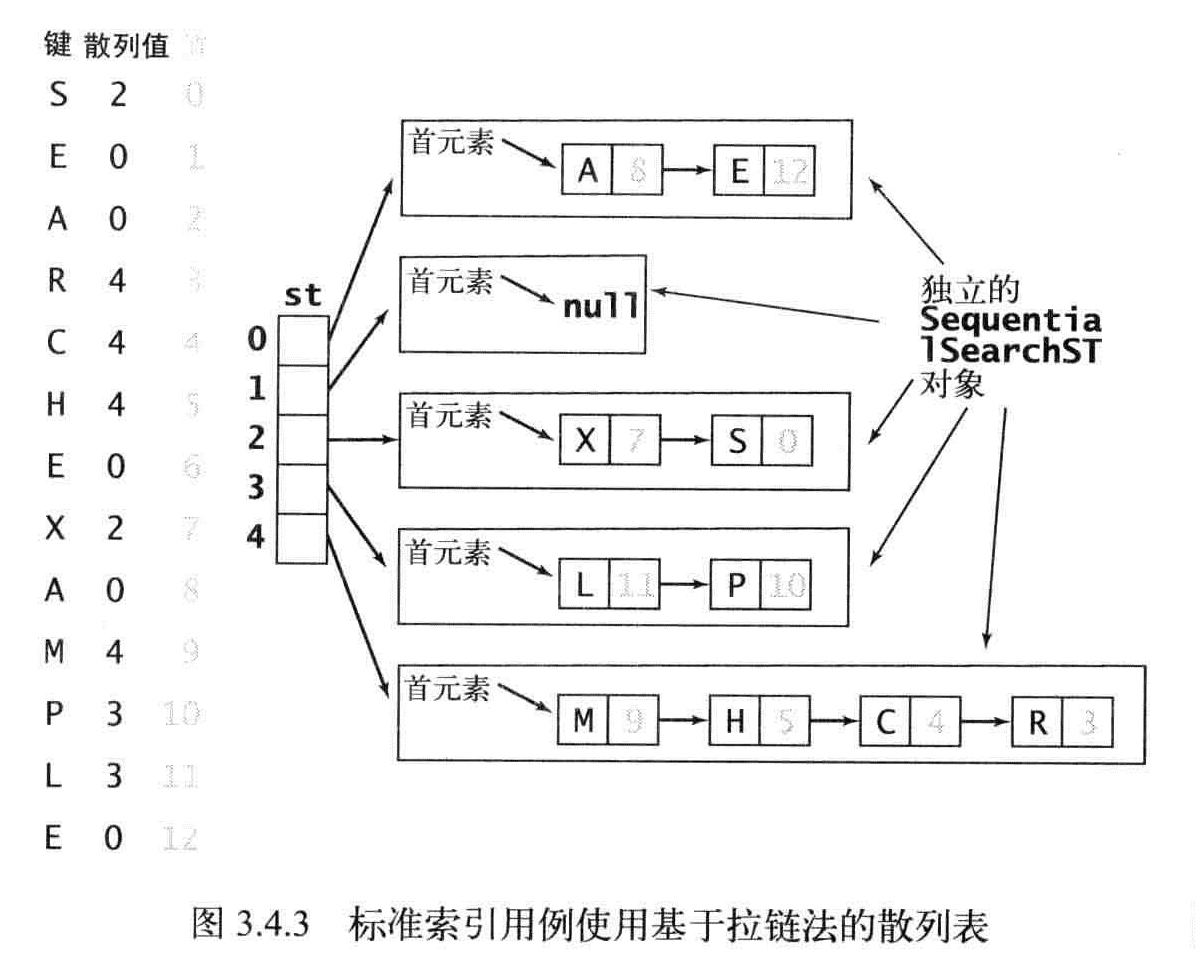
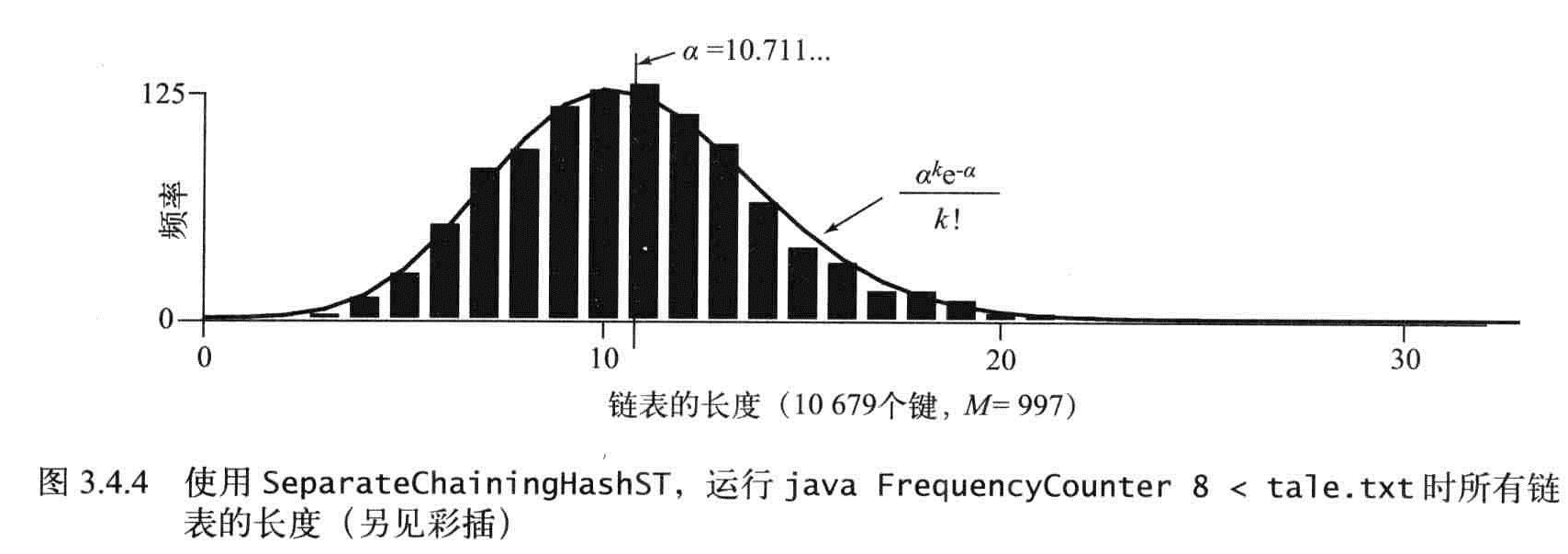
命题K:在一张含有M条链表和N个键的散列表中,任意一条链表中的键的数量均在N/M的常数因子范围内的概率无限趋向于1。
性质L:在一张含有M条链表和N个键的散列表中,未命中查找和插入操作所需的比较次数为~N/M
public class SeparateChainingHashSTNet<TKey, TValue>
{
private static readonly int INIT_CAPACITY = 4;
private int _length;
private int _capacity;
private SequentialSearchSTNet<TKey, TValue>[] st;
public int Length => _length;
public int Capacity => _capacity;
public SeparateChainingHashSTNet(): this(INIT_CAPACITY)
{
}
public SeparateChainingHashSTNet(int capacity)
{
this._capacity = capacity;
st =new SequentialSearchSTNet<TKey,TValue>[capacity];
for (int i = 0; i < capacity; i++)
st[i] = new SequentialSearchSTNet<TKey, TValue>();
}
private void resize(int chains)
{
SeparateChainingHashSTNet<TKey, TValue> temp = new SeparateChainingHashSTNet<TKey, TValue>(chains);
for (int i = 0; i < _capacity; i++)
{
foreach (TKey key in st[i].Keys)
{
temp.Add(key, st[i].Get(key));
}
}
this._capacity = temp.Capacity;
this._length = temp.Length;
this.st = temp.st;
}
/// <summary>
/// 计算散列值
/// </summary>
/// <param name="key"></param>
/// <returns></returns>
private int hash(TKey key)
{
return (key.GetHashCode() & 0x7fffffff) % _capacity;
}
public bool isEmpty() => Length == 0;
public bool Contains(TKey key)
{
if (key == null) throw new ArgumentException("argument to contains() is null");
return get(key) != null;
}
public TValue get(TKey key)
{
if (key == null) throw new ArgumentException("argument to get() is null");
int i = hash(key);
return st[i].Get(key);
}
public void Add(TKey key, TValue val)
{
if (key == null) throw new ArgumentException("first argument to put() is null");
if (val == null)
{
delete(key);
return;
}
if (_length >= 10 * _capacity) resize(2 * _capacity);
int i = hash(key);
if (!st[i].Contains(key)) _length++;
st[i].Add(key, val);
}
public void delete(TKey key)
{
if (key == null) throw new ArgumentException("argument to delete() is null");
int i = hash(key);
if (st[i].Contains(key)) _length--;
st[i].Delete(key);
if (_capacity > INIT_CAPACITY && _length <= 2 * _capacity) resize(_capacity / 2);
}
}
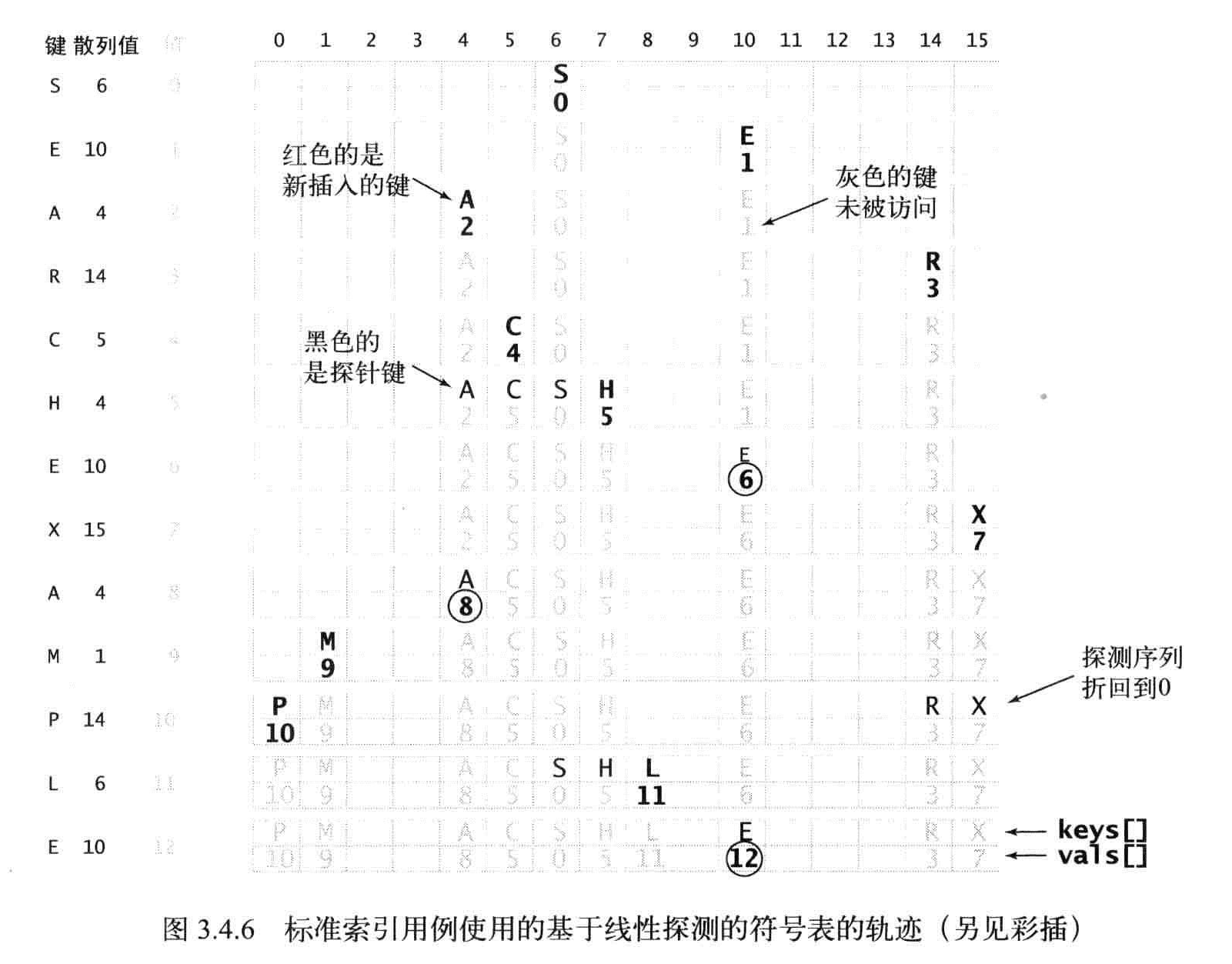
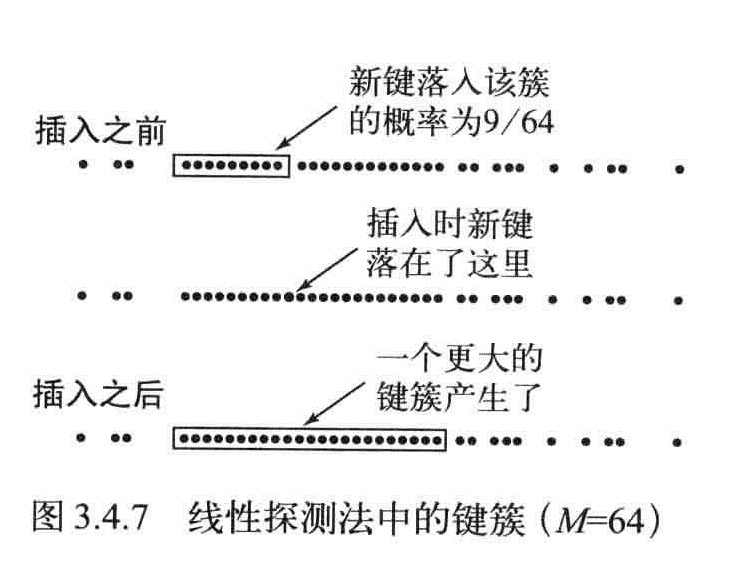
线性探测法
用大小为M的数组保存N个键值对,M>N,依靠数组中的空位解决碰撞冲突。开放地址散列表。
当发生碰撞时,直接使用散列标中下一个位置
键



public class LinearProbingHashSTNet<TKey, TValue>
{
private static readonly int INIT_CAPACITY = 4;
private int _length;
private int _capacity;
private TKey[] _keys;
private TValue[] _values;
public int Length => _length;
public int Capacity => _capacity;
public TKey[] Keys => _keys;
public TValue[] Values => _values;
public LinearProbingHashSTNet():this(INIT_CAPACITY)
{
}
public LinearProbingHashSTNet(int capacity)
{
_capacity = capacity;
_length = 0;
_keys = new TKey[capacity];
_values = new TValue[capacity];
}
public bool IsEmpty => _length == 0;
public bool Contains(TKey key)
{
if (key == null) throw new ArgumentException("argument to contains() is null");
return Get(key) != null;
}
private int hash(TKey key)
{
return (key.GetHashCode() & 0x7fffffff) % _capacity;
}
private void resize(int capacity)
{
LinearProbingHashSTNet<TKey, TValue> temp = new LinearProbingHashSTNet<TKey, TValue>(capacity);
for (int i = 0; i < _capacity; i++)
{
if (_keys[i] != null)
{
temp.Add(_keys[i], _values[i]);
}
}
_keys = temp.Keys;
_values = temp.Values;
_capacity = temp.Capacity;
}
public void Add(TKey key, TValue val)
{
if (key == null) throw new ArgumentException("first argument to put() is null");
if (val == null)
{
Delete(key);
return;
}
// double table size if 50% full
if (_length >= Capacity / 2) resize(2 * Capacity);
int i;
for (i = hash(key); _keys[i] != null; i = (i + 1) % _capacity)
{
if (_keys[i].Equals(key))
{
_values[i] = val;
return;
}
}
_keys[i] = key;
_values[i] = val;
_length++;
}
public TValue Get(TKey key)
{
if (key == null) throw new ArgumentException("argument to get() is null");
for (int i = hash(key); _keys[i] != null; i = (i + 1) % _capacity)
if (_keys[i].Equals(key))
return _values[i];
return default;
}
public void Delete(TKey key)
{
if (key == null) throw new ArgumentException("argument to delete() is null");
if (!Contains(key)) return;
// find position i of key
int i = hash(key);
while (!key.Equals(_keys[i]))
{
i = (i + 1) % _capacity;
}
// delete key and associated value
_keys[i] = default;
_values[i] = default;
// rehash all keys in same cluster
i = (i + 1) % _capacity;
while (_keys[i] != null)
{
// delete keys[i] an vals[i] and reinsert
TKey keyToRehash = _keys[i];
TValue valToRehash = _values[i];
_keys[i] = default;
_values[i] = default;
_length--;
Add(keyToRehash, valToRehash);
i = (i + 1) % _capacity;
}
_length--;
// halves size of array if it's 12.5% full or less
if (_length > 0 && _length <= _capacity / 8) resize(_capacity / 2);
}
}
字典总结

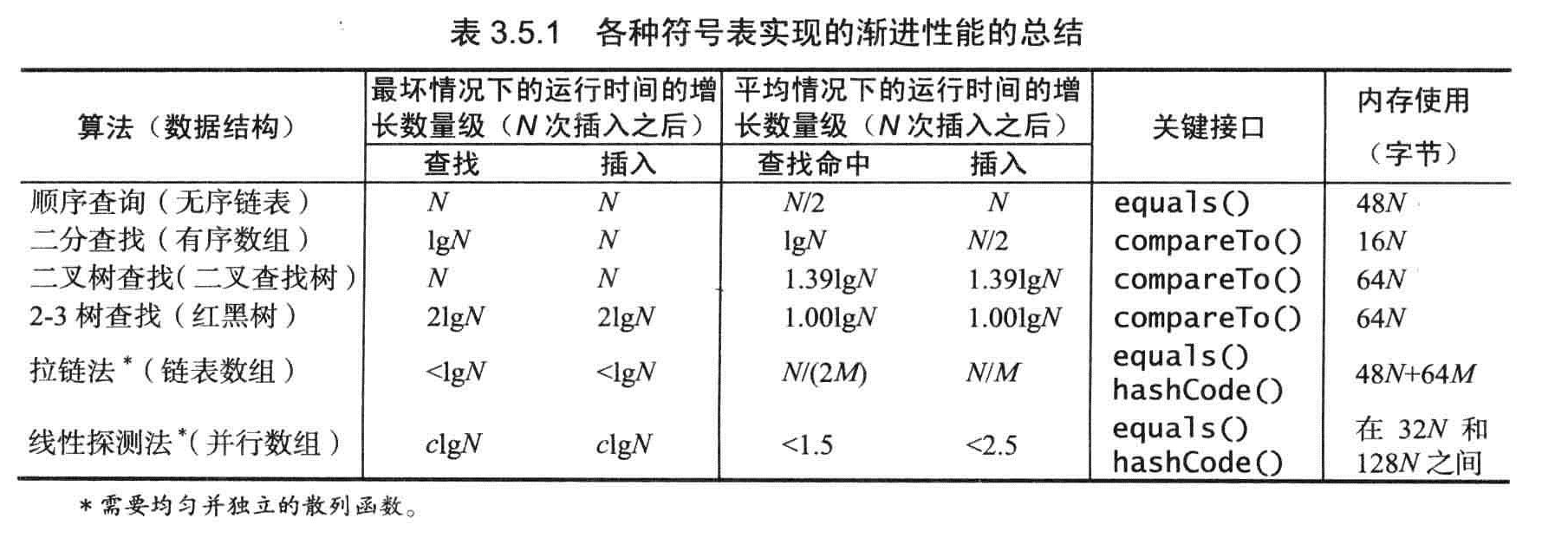
大多数程序员的第一选择都是散列标,然后才是红黑树。
