- 时空限制1s / 128MB
题目描述
如题,已知一个数列,你需要进行下面两种操作:
1.将某区间每一个数加上x
2.将某区间每一个数乘上x
3.求出某区间每一个数的和
输入输出格式
输入格式:第一行包含三个整数N、M、P,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数乘上k
操作2: 格式:2 x y k 含义:将区间[x,y]内每个数加上k
操作3: 格式:3 x y 含义:输出区间[x,y]内每个数的和对P取模所得的结果
输出格式:输出包含若干行整数,即为所有操作3的结果。
输入输出样例
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=8,M<=10
对于70%的数据:N<=1000,M<=10000
对于100%的数据:N<=100000,M<=100000
(数据已经过加强^_^)
样例说明:
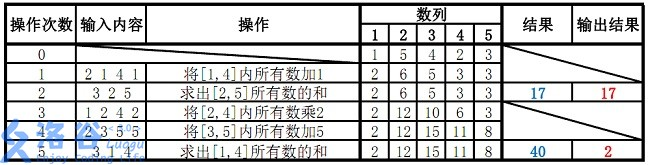
故输出应为17、2(40 mod 38=2)
--------------------------------------------------------------------------------------------------------
注意几个点:
(1)、乘法标记初始化为1;
(2)、在下传的时候先乘后加;
(3)、乘法下传里有几个操作:mult*mult、mult*sum、mult*tag、最后别忘了mult=1。
还是存个板子:

1 #include<stdio.h> 2 #include<string.h> 3 #define maxn 100010 4 struct node{ 5 int l,r; 6 long long sum,tag,mult; 7 }; 8 node tr[maxn*4]; 9 bool flag; 10 int n,m,a[maxn],p; 11 long long read(); 12 long long find(int,int,int); 13 void pushup(int); 14 void pushdownsum(int); 15 void pushdownmult(int); 16 void add(int,int,int,int); 17 void build(int,int,int); 18 int main(){ 19 n=read();m=read();p=read(); 20 for(int i=1;i<=n;i++) a[i]=read(); 21 build(1,n,1); 22 for(int i=1;i<=m;i++){ 23 int o=read(); 24 if(o==1){ 25 int x=read(),y=read(),k=read();flag=true; 26 add(x,y,k,1); 27 } 28 else if(o==2){ 29 int x=read(),y=read(),k=read();flag=false; 30 add(x,y,k,1); 31 } 32 else{ 33 int x=read(),y=read(); 34 printf("%lld ",find(x,y,1)); 35 } 36 } 37 return 0; 38 } 39 #define lson o<<1 40 #define rson o<<1|1 41 long long find(int l,int r,int o){ 42 if(l<=tr[o].l&&tr[o].r<=r) return tr[o].sum; 43 if(tr[o].mult!=1) pushdownmult(o); 44 if(tr[o].tag) pushdownsum(o); 45 int mid=(tr[o].l+tr[o].r)>>1; 46 if(l<=mid&&r>mid) return (find(l,r,lson)+find(l,r,rson))%p; 47 if(l<=mid) return find(l,r,lson); 48 if(r>mid) return find(l,r,rson); 49 } 50 void pushup(int o){ 51 tr[o].sum=(tr[lson].sum+tr[rson].sum)%p; 52 } 53 void pushdownmult(int o){ 54 long long k=tr[o].mult;tr[o].mult=1; 55 tr[lson].mult=(tr[lson].mult*k)%p;tr[rson].mult=(tr[rson].mult*k)%p; 56 tr[lson].sum=(tr[lson].sum*k)%p;tr[rson].sum=(tr[rson].sum*k)%p; 57 tr[lson].tag=(tr[lson].tag*k)%p;tr[rson].tag=(tr[rson].tag*k)%p; 58 } 59 void pushdownsum(int o){ 60 long long k=tr[o].tag;tr[o].tag=0; 61 tr[lson].tag=(tr[lson].tag+k)%p;tr[rson].tag=(tr[rson].tag+k)%p; 62 tr[lson].sum=(tr[lson].sum+k*(tr[lson].r-tr[lson].l+1))%p; 63 tr[rson].sum=(tr[rson].sum+k*(tr[rson].r-tr[rson].l+1))%p; 64 } 65 void add(int l,int r,int k,int o){ 66 if(l<=tr[o].l&&tr[o].r<=r){ 67 if(flag){ 68 tr[o].sum=(tr[o].sum*k)%p; 69 tr[o].mult=(tr[o].mult*k)%p; 70 tr[o].tag=(tr[o].tag*k)%p; 71 } 72 else{ 73 tr[o].sum=(tr[o].sum+(tr[o].r-tr[o].l+1)*k)%p; 74 tr[o].tag=(tr[o].tag+k)%p; 75 } 76 return; 77 } 78 if(tr[o].mult!=1) pushdownmult(o); 79 if(tr[o].tag) pushdownsum(o); 80 int mid=(tr[o].l+tr[o].r)>>1; 81 if(l<=mid) add(l,r,k,lson); 82 if(r>mid) add(l,r,k,rson); 83 pushup(o); 84 } 85 void build(int l,int r,int o){ 86 tr[o].l=l;tr[o].r=r;tr[o].mult=1; 87 if(l==r){ 88 tr[o].sum=a[l]; 89 return; 90 } 91 int mid=(l+r)>>1; 92 build(l,mid,lson);build(mid+1,r,rson); 93 pushup(o); 94 } 95 long long read(){ 96 long long ans=0,f=1;char c=getchar(); 97 while('0'>c||c>'9'){if(c=='-')f=-1;c=getchar();} 98 while('0'<=c&&c<='9')ans=ans*10+c-48,c=getchar();return ans*f; 99 }
