LinearRegressionWithRegularization

在线性回归的基础上加上正则项：

# -*-coding:utf-8 -*-
'''
Created on 2016年12月15日

@author: lpworkdstudy
'''
import numpy as np
from numpy.core.multiarray import dtype
import matplotlib.pyplot as plt


filename = "ex1data1.txt"
alpha = 0.01


f = open(filename,"r")
data = []
y = []
for item in f:
    item = item.rstrip().split(",")
    data.append(item[:-1])
    y.append(item[-1:])
Data = np.array(data,dtype= "float64")
Y = np.array(y,dtype = "float64")
Y = (Y-Y.mean())/(Y.max()-Y.min())
One = np.ones(Data.shape[0],dtype = "float64")
Data = np.insert(Data, 0, values=One, axis=1)
for i in range(1,Data.shape[1]):
    Data[:,i] = (Data[:,i]-Data[:,i].mean())/(Data[:,i].max()-Data[:,i].min())
theta = np.zeros((1,Data.shape[1]),dtype= "float64")

def CostFunction(Data,Y,theta):
    h = np.dot(Data,theta.T) 
    cost = 1/float((2*Data.shape[0]))*(np.sum((h-Y)**2) + np.sum(theta[0,1:]**2) )
    return cost
def GradientDescent(Data,Y,theta,alpha):
    costList = []
    for i in range(100000):
        temp = theta[0,0] - (alpha/Data.shape[0]*np.dot(Data[:,:1].T,(np.dot(Data,theta.T)-Y))).T
        theta[0,1:] =  (1-alpha/Data.shape[0])*theta[0,1:]- (alpha/Data.shape[0]*np.dot(Data[:,1:].T,(np.dot(Data,theta.T)-Y))).T
        theta[0,0] = temp
        cost = CostFunction(Data, Y, theta)
        costList.append(cost)
    plt.figure(1, figsize=(12,10), dpi=80, facecolor="green", edgecolor="black", frameon=True) 
    plt.subplot(111)
    
    plt.plot(range(100000),costList)
    plt.xlabel("the no. of iterations")
    plt.ylabel("cost Error")  
    plt.title("LinearRegression")  
    
    plt.savefig("LinearRegressionRegularized.png")
    return theta
if __name__ == "__main__":
    weight = GradientDescent(Data,Y,theta,alpha)
    print weight
    cost = CostFunction(Data, Y, weight)
    print cost

运行得出损失函数随迭代次数的变化曲线如下图：

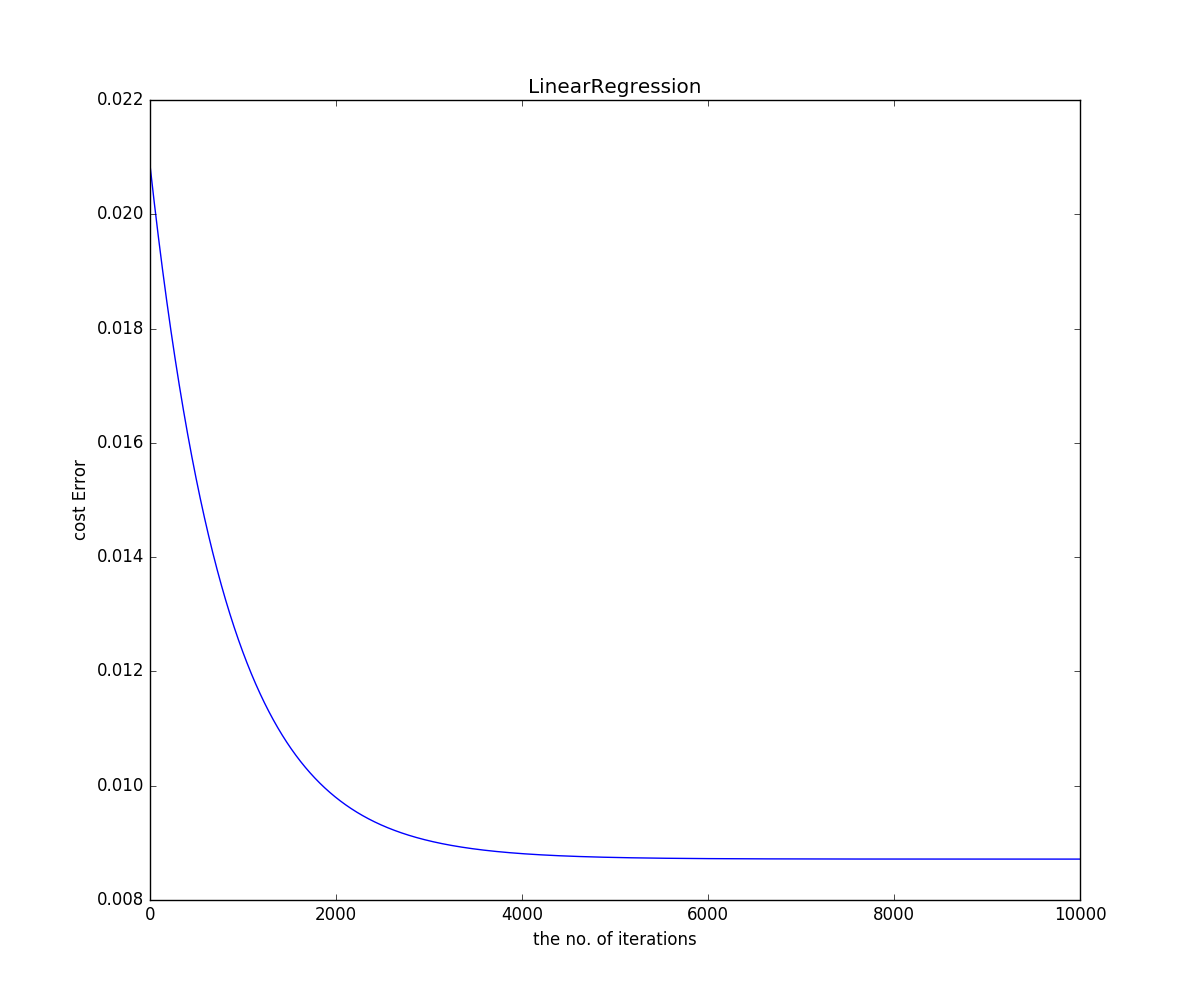
可以看出加入正则项并没有优化我们的模型，反而产生了不好的
影响，所以我们在解决问题时，不要盲目使用正则化项。