排序
排序是将一个无序的序列按照一定顺序排列成一个有序序列的操作。其中,升序排序是指序列按从小到大排序,降序排序是指序列按从大到小排序。
若一个序列中存在相同的两个元素,在排序后:
a. 若这两个元素先后顺序不变,则称该排序算法是稳定的。
b. 若这两个元素先后顺序变化,则称该排序算法是不稳定的。
例如:对于序列(56, 34, 47, 23, 66, 18, 82, 47)中有两个47,在第一个47下划线。
若排序结果为(18, 23, 34, 47, 47, 56, 66, 82),即两个47的先后顺序不变,则该排序算法是稳定的;
若排序结果为(18, 23, 34, 47, 47, 56, 66, 82),即两个47的先后顺序变化,则该排序算法是不稳定的。
常见的排序算法有8种:冒泡排序、选择排序、插入排序、希尔排序、快速排序、归并排序、堆排序和基数排序。
| 平均时间复杂度 | 最好情况 | 最坏情况 | 额外内存 | 稳定性 | |
| 冒泡排序 | O(n2) | O(n) | O(n2) | × | √ |
| 选择排序 | O(n2) | O(n2) | O(n2) | × | × |
| 插入排序 | O(n2) | O(n) | O(n2) | × | √ |
| 希尔排序 | O(n log n) | O(n log n) | O(n log n) | × | × |
| 快速排序 | O(n log n) | O(n log n) | O(n2) | × | × |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | √ | √ |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | × | × |
| 基数排序 | O(n) | O(n) | O(n) | √ | √ |
冒泡排序
冒泡排序的思想是:将序列中相邻两个元素进行比较,若为逆序,则交换位置。所以,一趟冒泡排序可以将序列中最大(或最小)的元素排在序列最末端。
若一个序列有n个元素,则需要进行(n - 1)趟冒泡排序。其中,第一趟冒泡排序需要比较(n - 1)次,第二趟冒泡排序需要比较(n - 2)次......也就是说,(n - 1)趟冒泡排序需要比较n * (n - 1) / 2次,最坏情况下需要交换n * (n - 1) / 2次。
为了防止冒泡排序趟数过多,可以对冒泡排序进行优化。若一趟冒泡排序中没有进行过元素的交换,则表示该序列已经有序,无需再进行排序。所以可以设置一个标识位,用于标识当前冒泡排序是否交换过元素,若没有交换过,直接退出排序。
冒泡排序的代码如下:

1 public static void bubbleSort(int[] arr) { 2 // 标识位 3 boolean flag; 4 for (int i = arr.length - 1; i >= 1; i--) { 5 // 标识位初值置为false 6 flag = false; 7 for (int j = 0; j < i; j++) { 8 // 相邻两个数进行比较 9 if (arr[j] > arr[j + 1]) { // 降序则为arr[j] < arr[j + 1] 10 int temp = arr[j]; 11 arr[j] = arr[j + 1]; 12 arr[j + 1] = temp; 13 // 若交换过元素,则标识位置为true 14 flag = true; 15 } 16 } 17 // 如果标识位为false,表示当前冒泡排序没有交换过元素,即序列已经有序,直接退出 18 if (! flag) break; 19 } 20 }
例如:对序列(5, 8, 3, 4, 9, 2, 7, 6, 1)进行升序排序。
第一趟冒泡排序的过程为:
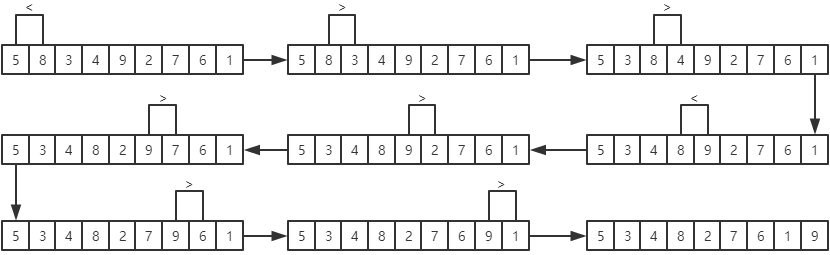
每一趟冒泡排序的结果为:

选择排序
选择排序的思想是:每次从序列中找到最大(或最小)的元素与最末端的元素交换位置。所以,一趟选择排序可以将序列中最大(或最小)的元素排在序列最末端。
若一个序列有n个元素,则需要进行(n - 1)趟选择排序。其中,第一趟选择排序需要比较(n - 1)次,第二趟选择排序需要比较(n - 2)次......也就是说,(n - 1)趟选择排序需要比较n * (n - 1) / 2次。最坏情况下每一趟选择排序需要进行一次交换,(n - 1)趟选择排序需要进行(n - 1)次交换。
选择排序的代码如下:

1 public static void selectSort(int[] arr) { 2 for (int i = arr.length - 1; i > 0; i--) { 3 // 遍历序列找到最小元素所在的位标 4 int index = i; 5 for (int j = 0; j < i; j++) { 6 if (arr[index] < arr[j]) index = j; // 降序则为arr[index] > arr[j] 7 } 8 // index == i表示最小元素所在的位标刚好在最末端,无需交换 9 if (index == i) continue; 10 int temp = arr[index]; 11 arr[index] = arr[i]; 12 arr[i] = temp; 13 } 14 }
例如:对序列(5, 8, 3, 4, 9, 2, 7, 6, 1)进行升序排序。
第一趟选择排序的过程为:
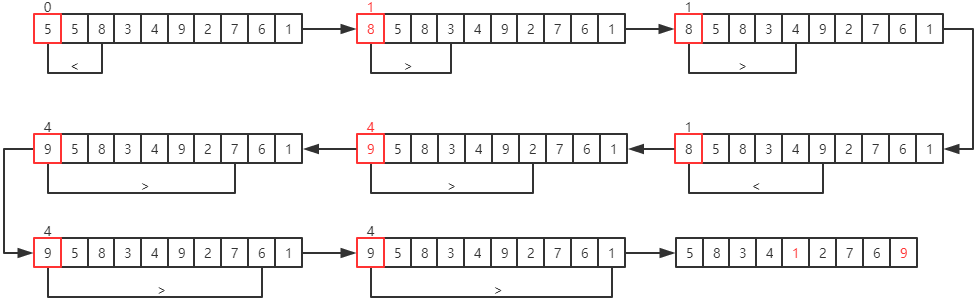
每一趟选择排序的结果为:

插入排序
插入排序的思想是:在序列前面的部分找到合适的位置插入元素,使得序列前面的部分变得有序。
若一个序列有n个元素,则需要进行(n - 1)趟插入排序。在最坏的情况下,第一趟插入排序需要比较1次,移位1次,第二趟插入排序需要比较2次,移位2次......也就是说,在最坏的情况下,(n - 1)趟插入排序需要比较n * (n - 1) / 2次,移位n * (n - 1) / 2次。
插入排序的代码如下:

1 public static void insertSort(int[] arr) { 2 for (int i = 1; i < arr.length; i++) { 3 // 将当前元素作为哨兵 4 int temp = arr[i]; 5 int index = i; 6 while (index >= 1 && temp < arr[index - 1]) { // 降序则为temp > arr[index - 1] 7 // 若前一个当前元素比哨兵大,则后移 8 arr[index] = arr[index - 1]; 9 index--; 10 } 11 // 找到合适的位置,将哨兵插入 12 arr[index] = temp; 13 } 14 }
例如:对序列(5, 8, 3, 4, 9, 2, 7, 6, 1)进行升序排序。
第一趟插入排序的过程为:

每一趟插入排序的结果为:

希尔排序
希尔排序是对插入排序的一种改进,其思想是:将序列划分按照增量d(初始值为序列长度的一半)划分成d个子序列,并对每个子序列进行插入排序,之后对增量d不断减半,重复这一过程直到d减少到1,对整个序列进行一次插入排序。
希尔排序与插入排序的不同之处在于,插入排序每次对相邻元素进行比较,元素最多只移动了一个位置,而希尔排序每次对相隔较远距离(即增量d)的元素进行比较,使得元素移动时能跨过多个元素,实现宏观上的调整。当增量减小到1时,序列已基本有序,最后一趟希尔排序可以说是接近最好情况的直接插入排序。一般情况下,可将前面各趟希尔排序的调整看作是最后一趟希尔排序的预处理,看似多做了几趟插入排序,实际上比只做一次插入排序效率更高。
希尔排序的代码如下:

1 public static void shellSort(int[] arr) { 2 // 增量d的初始值为序列长度的一半,之后每次增量d都减半 3 for (int d = arr.length / 2; d > 0; d /= 2) { 4 for (int i = d; i < arr.length; i++) { 5 // 对每一个子序列进行插入排序 6 int temp = arr[i]; 7 int j = i; 8 while (j >= d && temp < arr[j - d]) { // 降序则为temp > arr[j - d] 9 arr[j] = arr[j - d]; 10 j -= d; 11 } 12 arr[j] = temp; 13 } 14 } 15 }
例如:对序列(5, 8, 3, 4, 9, 2, 7, 6, 1)进行升序排序。
第一趟希尔排序的过程为:
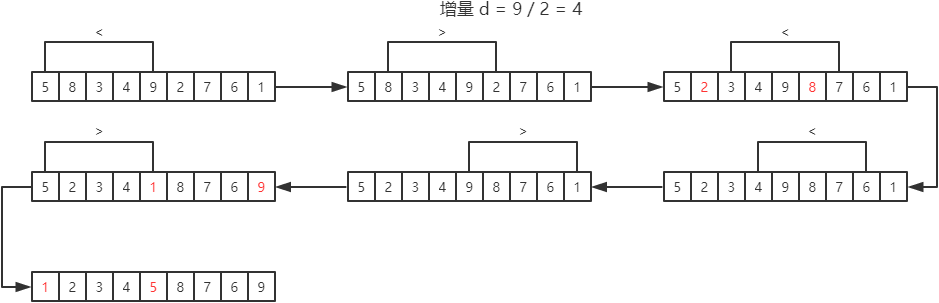
每一趟希尔排序的结果为:

快速排序
快速排序是对冒泡排序的一种改进,其思想是:从序列中选定一个元素作为枢轴,将其他元素与枢轴进行比较,分为比枢轴小和比枢轴大两个子序列,之后对每个子序列做同样的操作。
快速排序的最好情况是,每一趟快速排序都能划分出同等大小的两个子序列;最坏情况是,每一趟快速排序取到的枢轴都是最值,此时快速排序就退化成冒泡排序。
以第一个(或者最后一个)元素作为枢轴,当原序列已经有序时,每一趟快速排序取到的枢轴就都是序列中的最值,此时快速排序就退化成冒泡排序。
快速排序的代码如下(取序列第一个元素作为枢轴):

1 /** 2 * @param l 序列第一个元素的位标 3 * @param h 序列最后一个元素的位标 4 */ 5 public static void quickSort(int[] arr, int l, int h) { 6 // l < h,即h + 1 - l > 1,表示划分的子序列中至少有2个元素 7 if (l < h) { 8 // 定义low和high分别指向子序列的两端 9 int low = l, high = h; 10 // 取子序列的第一个元素作为枢轴 11 int pivot = arr[low]; 12 // low == high时循环结束 13 while (low < high) { 14 // 先从high开始往前找,找到第一个比枢轴小的元素放在arr[low]处 15 while (low < high && arr[high] >= pivot) high--; // 降序则arr[high] <= pivot 16 arr[low] = arr[high]; 17 // 之后从low开始往后找,找到第一个比枢轴大的元素放在arr[high]处 18 while (low < high && arr[low] <= pivot) low++; // 降序则arr[low] >= pivot 19 arr[high] = arr[low]; 20 } 21 // low和high相遇的位置即为枢轴应该放入的位置 22 arr[low] = pivot; 23 // 此时将序列划分为(l, low - 1)和(low + 1, h)两个子序列,再分别对两个子序列递归划分 24 quickSort(arr, l, low - 1); 25 quickSort(arr, low + 1, h); 26 } 27 }
例如:对序列(5, 8, 3, 4, 9, 2, 7, 6, 1)进行升序排序。
第一趟快速排序的过程为:

每一趟快速排序的结果为:

可以看到,在这个例子中,除了第一趟快速排序外,之后的每一趟排序都无法划分出两个子序列。
归并排序
归并排序的思想是:指序列递归分解成若干个长度大致相等的子序列,然后将各个子序列合并,并在合并时进行排序,最终合并为整体有序序列的过程。
归并排序的代码如下:

1 public static void mergeSort(int[] arr, int low, int high, int[] temp) { 2 // low < high,即high + 1 - low > 1,表示序列中元素至少有2个元素 3 if (low < high) { 4 // 分组:将一个序列分为同等大小的两个子序列,并对子序列进行同样的操作 5 int middle = (low + high + 1) / 2; 6 mergeSort(arr, low, middle - 1, temp); 7 mergeSort(arr, middle, high, temp); 8 // 合并:将两个有序序列合并为一个有序序列 9 int i = low, j = middle, k = 0; 10 while (i < middle && j <= high) { 11 if (arr[i] <= arr[j]) temp[k++] = arr[i++]; // 降序则arr[i] >= arr[j] 12 else temp[k++] = arr[j++]; 13 } 14 while (i < middle) temp[k++] = arr[i++]; 15 while (j <= high) temp[k++] = arr[j++]; 16 System.arraycopy(temp, 0, arr, low, k); 17 } 18 }
例如:对序列(5, 8, 3, 4, 9, 2, 7, 6, 1)进行升序排序。
归并排序的过程为:


堆排序
堆排序是利用堆特性的一种选择排序,其思想是:先将原序列调整成堆(升序为大顶堆,降序为小顶堆),之后每一次将根结点与最后一个结点交换,将最后一个结点“取出”,剩余的结点再调整成堆。
堆排序的代码如下:

1 public static void adjust(int[] arr, int len, int i) { 2 int temp = arr[i]; 3 while (i <= len / 2 - 1) { 4 int j = i * 2 + 1; 5 if (j + 1 < len && arr[j] < arr[j + 1]) j++; // 降序则为arr[j] > arr[j + 1] 6 if (temp >= arr[j]) break; // 降序则为temp <= arr[j] 7 arr[i] = arr[j]; 8 i = j; 9 } 10 arr[i] = temp; 11 }

1 public static void heapSort(int[] arr) { 2 // 将整个无序序列调整成堆,需要对所有非叶子结点进行调整,其中arr.length / 2 - 1为最后一个非叶子结点 3 for (int i = arr.length / 2 - 1; i >= 0; i--) { 4 adjust(arr, arr.length, i); 5 } 6 for (int i = arr.length - 1; i > 0; i--) { 7 int temp = arr[i]; 8 arr[i] = arr[0]; 9 arr[0] = temp; 10 adjust(arr, i, 0); 11 } 12 }
例如:对序列(5, 8, 3, 4, 9, 2, 7, 6, 1)进行升序排序。
将无序序列调整为大顶堆:
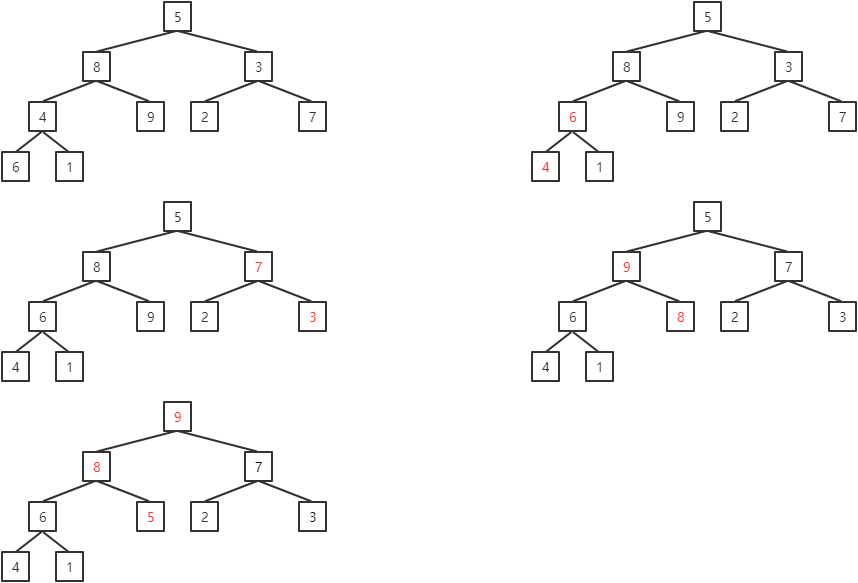
第一趟堆排序的过程为:
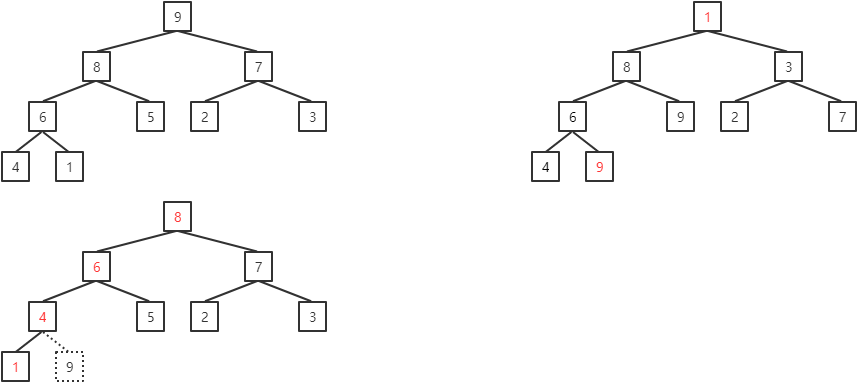
每一趟堆排序的结果为:

基数排序
基数排序的思路是:将元素看成由多个关键字组成,将所有元素按从低位关键字开始的每一位关键字进行排序。以数字为例,数字可以看作由个位数、十位数、百位数等组成,而每一位都是0-9的数字。先将序列中所有数字按个位数排序,再按十位数排序,......,最后按最高位排序。
基数排序的趟数与序列中元素的个数无关,而与最大元素中关键字的个数有关。例如,一个数字序列中最大的数字有k位数,则对该序列排序时需要进行k趟基数排序。
在一趟基数排序中,首先需要遍历所有元素,统计每个关键字中元素的个数,然后计算每个关键字的起始下标,最后再一次遍历所有元素,按照记录的起始下标将元素放入数组中。
基数排序(数字序列)的代码如下:

1 public static void radixSort(int[] arr) { 2 // 找到最大的元素 3 int max = arr[0]; 4 for (int i = 1; i < arr.length; i++) { 5 if (max < arr[i]) max = arr[i]; 6 } 7 // 获取排序的趟数 8 int len = (max + "").length(); 9 // 创建辅助数组 10 int[] temp = new int[arr.length]; 11 for (int k = 1, count = 1; count <= len; k *= 10, count++) { 12 int[] pos = new int[10]; 13 // 记录每个关键字的元素个数 14 for (int i : arr) pos[i / k % 10]++; 15 // 计算每个关键字的起始位标 16 pos[9] = arr.length - pos[9]; // 降序则为pos[0] = arr.length - pos[0]; 17 for (int i = 8; i >= 0; i--) pos[i] = pos[i + 1] - pos[i]; // 降序则为for (int i = 1; i <= 9; i++) pos[i] = pos[i - 1] - pos[i]; 18 // 将每个元素按起始位标插入序列中 19 for (int i : arr) temp[pos[i / k % 10]++] = i; 20 System.arraycopy(temp, 0, arr, 0, arr.length); 21 } 22 }
例如,对(337, 332, 132, 267, 262, 164, 260, 167)进行升序排序。
第一趟基数排序的过程为:
a. 统计个位数中每个值的元素个数:个位数为0的有1个,个位数为2的有3个,个位数为4的有1个,个位数为7的有3个。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 0 | 3 | 0 | 1 | 0 | 0 | 3 | 0 | 0 |
b. 计算每个值的起始下标:个位数为0的从下标0开始,个位数为2的从下标1开始,个位数为4的从下标4开始,个位数为7的从下标5开始。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | 1 | 4 | 4 | 5 | 5 | 5 | 8 | 8 |
c. 再次遍历序列,将所有元素插入到辅助数组中:元素插入后,对应位标加1。
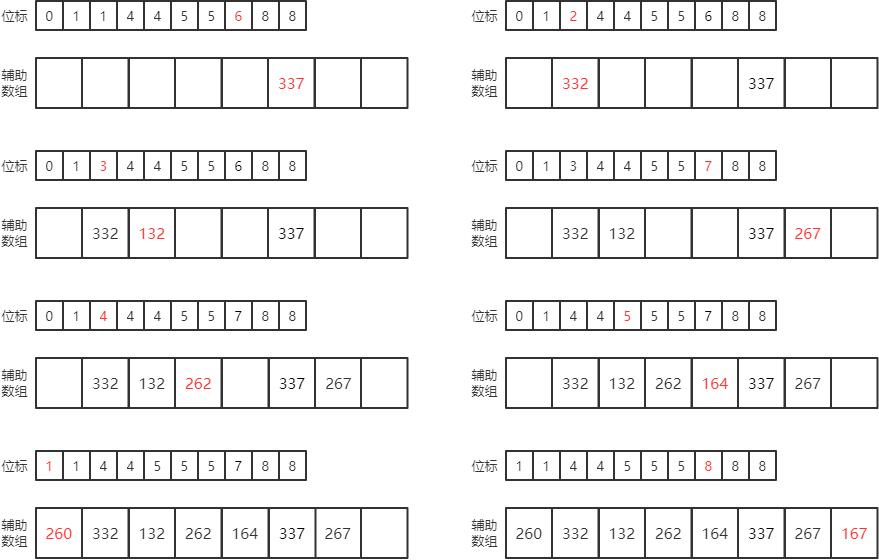
每一趟基数排序的结果为:

排序算法效率测试
随机生成一个有100000个元素的序列,其中元素的取值范围为[0, 100000),统计八种算法对该序列进行升序排序耗费的时间。

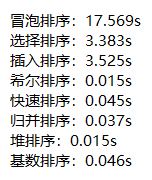
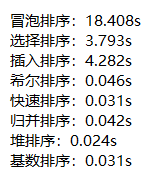

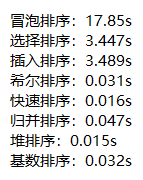
大致上可以看出,对同一个序列进行升序排序,冒泡排序耗费的时间最大,而归并排序、堆排序、基数排序耗费的时间最短。
