队列

队列

　　队列是一种常见的线性结构，遵循先进先出的原则，即先存入队列的元素要先取出，后存入队列的元素要后取出。

　　队列的插入操作称为入队，入队在队尾进行；队列的删除操作称为出队，出队在队头进行。因此需要front和rear两个变量分别记录队头和队尾的位置，front随着出队操作而改变，rear随着入队操作而改变。

　　具体操作如下：

　　1. 定义队列时需要定义三个变量：存储容量maxSize、队头位标front、队尾位标rear。其中front存储队头元素的位标，rear存储队尾元素下一位置的位标。

　　2. 入队：先判断队列是否已满，没有满就可以进行入队操作。元素入队后，rear需要自增，即rear++。

　　3. 出队：先判断队列是否为空，不为空就可以进行出队操作。元素出队后，front需要自增，即front++。

　　4. 判空：front == rear。

　　5. 判满：rear == maxSize。

　　以一个存储容量为5的队列为例，初始化后front = rear = 0：

　　

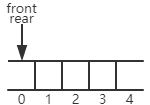
　　插入一个元素，rear自增：

　　

　　弹出一个元素，front自增：

　　

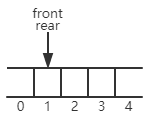
　　而当在4号位置插入元素后，rear = 5，此时表示队列已满：

　　

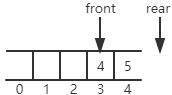
　　可以发现，front前面的空间已经无法再使用。

　　也就是说，队列每个存储空间只能使用一次，无法复用。这是队列的一个重大缺陷。

代码实现

　　入队：

public void enQueue(E e) {
    if (isFull()) throw new QueueException("队列已满！");
    elem[rear++] = e;
}

　　出队：

public E deQueue() {
    if (isEmpty()) throw new QueueException("队列为空！");
    E e = elem[front];
    elem[front++] = null;
    return e;
}

　　获取队头元素：

public E getHead() {
    if (isEmpty()) return null;
    return elem[front];
}

　　判空：

public boolean isEmpty() {
    return front == rear;
}

　　判满：

public boolean isFull() {
    return rear == maxSize;
}

循环队列

　　循环队列是对队列的一种改进，具体为：rear不再是普通的自增，而是循环自增，即rear = (rear + 1) % maxSize。这样就可以实现队列的复用。

　　以存储容量为5的循环队列为例：

　　

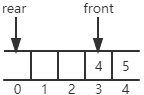
　　可以看到，插入元素5后，rear循环自增，回到了0号单元的位置。

　　但是，在这种情况下：

　　

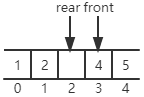
　　如果再插入一个元素，就会变成：

　　

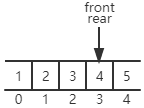
　　可以看到，这时队列已满，front == rear。

　　新的问题出现了：front == rear时，无法确定队列为空还是队列已满。此时有两种解决思路：

　　1. 增加变量length表示队列中元素的个数。length == 0就表示队列为空，length == maxSize就表示队列已满。

　　2. 预留一个空间。front == rear表示队列为空，front == (rear + 1) % maxSize表示队列已满。

代码实现

　　采用第二种解决思路，预留一个空间。

　　入队：

public void enQueue(E e) {
    if (isFull()) throw new QueueException("队列已满！");
    elem[rear] = e;
    rear = (rear + 1) % maxSize;
}

　　出队：

public E deQueue() {
    if (isEmpty()) throw new QueueException("队列为空！");
    E e = elem[front];
    elem[front] = null;
    front = (front + 1) % maxSize;
    return e;
}

　　获取队头元素：

public E getHead() {
    if (isEmpty()) return null;
    return elem[front];
}

　　判空：

public boolean isEmpty() {
    return front == rear;
}

　　判满：

public boolean isFull() {
    return front == (rear + 1) % maxSize;
}