上一篇 :
栈论 : 递归与栈式访问,如何用栈实现所有递归操作(幼儿园题目篇)
题目2
题目2和题目1最大的不同点是访问顺序变了。
我们对应的伪代码应该如下:
1,2,3表示的是先递归读取左子树,再是右子树,最后读取自己
void postOrderRead(BiTree tree){
if(tree == NULL){
return;
}
preOrderRead(tree -> lchild); //1
preOrderRead(tree -> rchild);//2
visit(tree);//3
}
看完上一道题的解析,应该熟能生巧了吧~
首先,我们列出每个栈帧应该具有的信息 :
1.当前节点
其次,我们理一下逻辑思路
下面的左子函数 = 左节点的子函数
首先,因为父函数中对节点的读取是在子函数退出之后的(3在1和2之后),所以父函数的栈帧在子函数栈帧入栈时不能出栈(不能退出),要等待子函数出栈,
操作完3之后才能出栈。如果我们现在我们从栈中访问了一个节点(注意是访问,不是弹出,因为父栈帧不能随意弹出),因为是后序遍历,所以要访问左子树先
也就是执行1处,所以总是要把包含左子节点的栈帧入栈。只有等到左子树是空才停止。
但是现在有一个问题,当我们访问到一个节点,我们怎么知道他的子函数栈帧该不该创建呢(子函数调用),因为此时可能是子函数调用过并退出,当前栈帧才露出来给我们获取到。另一种是子函数还没有调用,现在的栈帧是刚创建的,需要马上调用子函数。总结来说就是我们在当前节点不知是该调用子函数还是自己退出。造成这种情况的原因是,因为函数是顺序执行的,即使在同一个栈帧中,这段栈帧对应的程序是可以知道当前程序执行到的行号的。也就是说知道是否该调用子函数。而我们从栈帧得到栈帧,如果不带有类似行号的信息,根本不知道是否该调用子函数。
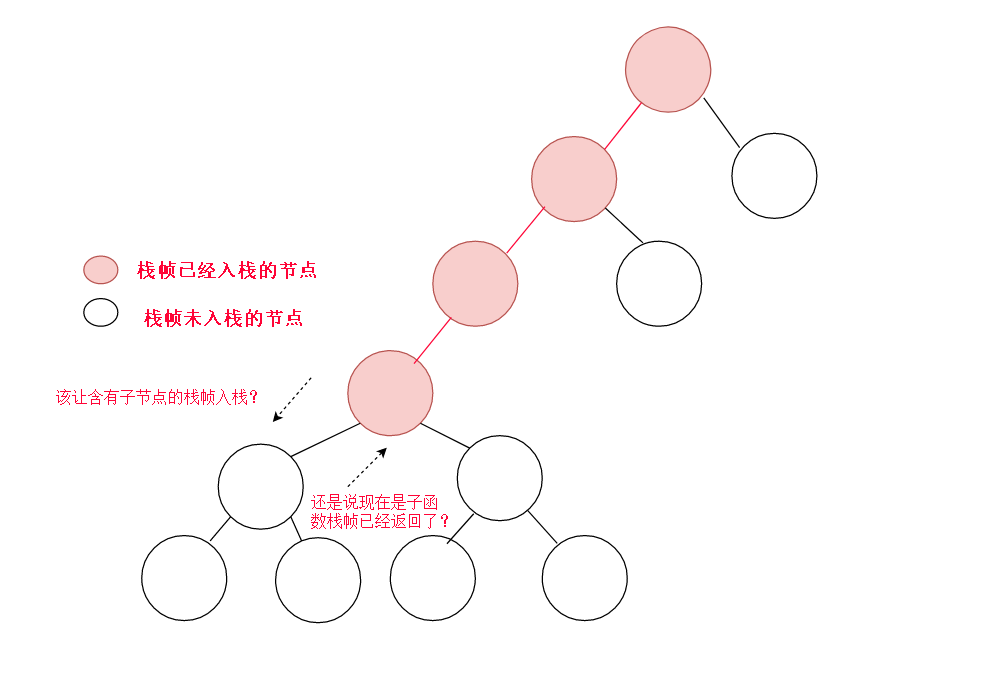
所以,栈帧里的信息,我们需要修改一下。
每个栈帧应该具有的信息 :
1.当前节点
2.当前节点是否已经调用过左/右子函数
第二点和行号有差不多的功能,但我们只需要是否调用过子函数的信息,行号太细了,可以但是没必要。
那么用什么来存储这个信息呢?
我的想法是用一个int型的变量,一个int型的变量一般是32位,也就是说他可以存储32个“是与否的信息”。
我用最低位为1表示还需要将左子函数栈帧入栈(还没调用过),为0表示已经把左子函数栈帧入栈了。
依次类推,第二位来对应右子函数。

你可能会问我这样选是否合理,我个人觉得还是相对合理的。
原因如下:
1.首先存储信息的载体体积较小,只用一个变量,充分利用每一位的信息。
2.其次是虽然每次获取信息都需要进行与掩码的操作(例如 A | (00000000 00000000 00000000 00000001) = 是否左子函数栈帧入栈),但是这样的操作耗时还是相对较少的。相比之下,如果我们用了很多个变量,频繁读取这些变量的时候,高速缓存的cache line 可能就会被提前填满,导致我们缓存的优势发挥效能降低,CPU运行速度下降。而且 | 操作在硬件层面讲是时间复杂度为O(1)的操作,因为每一位的信号都可以并行通过与门。而移位则需要等待下一位的触发器接受到上一位的触发器信息,上一位的触发器才能接受上上一位的触发器信息,存在等待问题,所以硬件层面的时间复杂度是O(n)。选与操作还是比较好的。当然,这只是从我有限的硬件知识推理分析的,并没有考虑操作系统之类的因素,如果有说错的地方请赐教。当然你也可以不运算,直接将这个int的不同值对应不同的情况,比如0表示调用左子函数,1不是不要,2表示调用右子函数,3表示不要......但是这样没有了0和1这样相反的思维逻辑条理性,而且情况一多处理麻烦。

实现代码如下 :
栈帧定义 :
typedef struct FunctionFrame {
BiTNode * node;
int tag; // 标志是应该往右走还是往左走
};
具体实现
Stack stack;
FunctionFrame frame;
int initial;
initial = 0b0011; //初始值 表示两边都还要调用
init(stack);
frame = {&node, initial};
push(stack, &frame);
while (!stackEmpty(stack)) { //栈不空表示还有函数在调用中
FunctionFrame* frame = getTop(stack); //不是弹出的访问
if (frame -> tag & 0b0001) { //如果最低位是1
if (frame ->node ->lchild != NULL) { //左孩子节点不为空
FunctionFrame* lc = (FunctionFrame*) malloc(sizeof(FunctionFrame)); //创建左子节点的函数栈帧
lc->node = frame->node->lchild;
lc->tag = initial;
push(stack, lc); // 左子函数栈帧入栈
frame->tag = frame->tag & 0b0010; //将最低位(调用左子函数的标志)抹除掉
continue; //左子函数栈帧入栈 右子函数就不要入了,因为要等待左子函数调用完右边才能调用
}
}
//如上,以此类推
if (frame ->tag & 0b0010) {
if (frame->node->rchild != NULL) {
FunctionFrame* rc = (FunctionFrame*)malloc(sizeof(FunctionFrame));
rc->node = frame->node->rchild;
rc->tag = initial;
push(stack, rc);
frame->tag = frame->tag & 0b0001;
continue;
}
}
visit(frame -> node);
pop(stack);
}
下一篇 :
栈论 : 递归与栈式访问,如何用栈实现所有递归操作(幼儿园题目篇,题目3)
护眼绿:
没人看的结语:
首先很感谢你看到这里,辛苦了。
文章中某些地方可能不正确或不准确,代码也可能不够高效可读,希望读者能够帮忙指正,共同学习进步。