上一章我们讲到并归排序,并归排序的重要思想是对大问题进行分解,解决分解出来的小问题达到解决大问题的效果
但是归并排序明显存在的缺点是需要一个额外的数组空间来存储临时数据
为此,我们希望找到一种算法,平均时间复杂度为 N * logN,同时空间复杂度为常数级
之前我们探讨过并归排序的时间复杂度组成 , 对大小为 N 的数组进行均分,直至均分到 1 为止,总共分成 (log2)(N)次
对每次均分出来的结果进行线性操作使其有序,当 N 趋紧无穷时,总时间复杂度 = 线性 * 操作次数 = N * (log N)
对于快速排序,我们也想要做到上述操作,而且不用额外庞大的临时空间,但实际上,是不可能做到完全均分的,这和我们快速排序的操作有关
快速排序的操作核心思想是在数组中找到一个数,称之为基准数,把比基准数要小的元素移到数组的左边,比基准数要大的元素移到右边
这样我们的数组会被分割成 : (其中8是基准数)
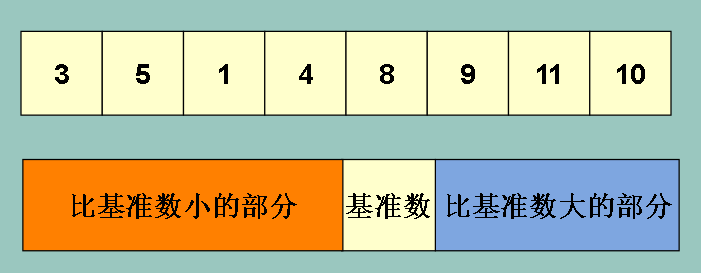
同样的,对左边的橙色部分和右边的蓝色部分采取同样的方法
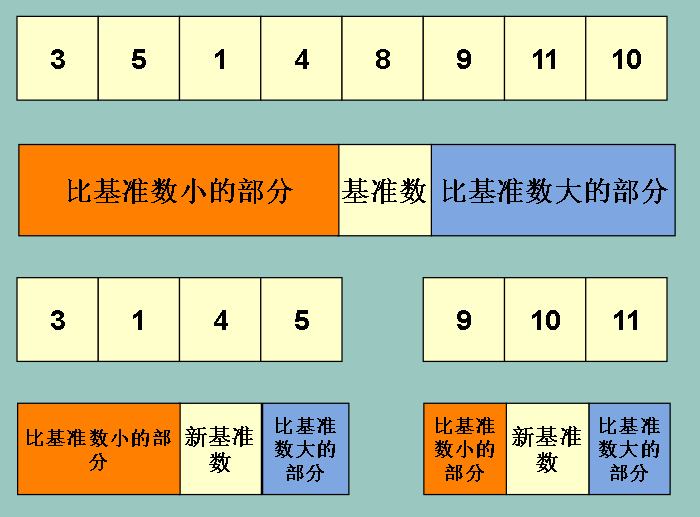
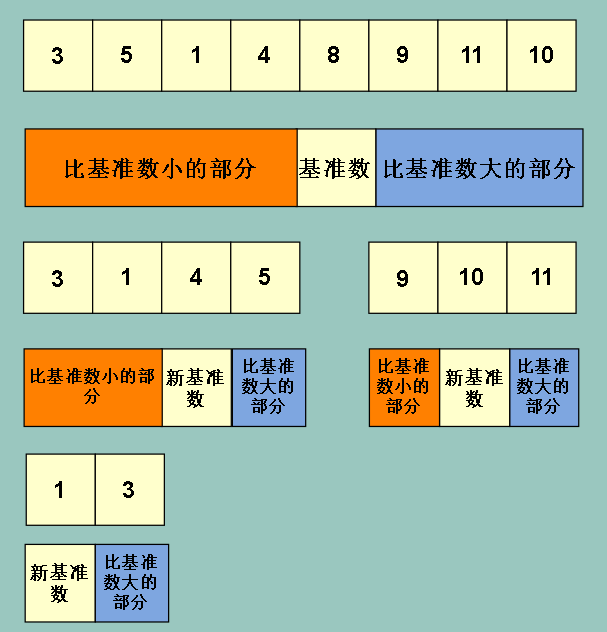
为了方便 ,我们在下文称左边比基准数小的区域为 ‘左边区域’,比基准数大的区域为‘右边区域’
从图上可以看出,当左边区域或者右边区域的大小为1,也就是只有一个元素的时候,选取基准数和分出左右区域的操作就停止了
最终得出我们想要的排序结果(图中框选所示)

但是我们可以发现,每次分割出的左边橙色部分总是不一定等于右边蓝色部分,也就是说,每次操作不一定均分我们的数组
所以我们完成的可能不只 (log2) (n) 次线性操作
那我们怎么能尽可能打出 (log2) (n) 次线性操作呢?
快速排序的关键无非是两个 : 基准数的选取 和 分割策略
1.分割策略 :
在吴伟民老师的《数据结构》一书中,使用的分割策略如下 :
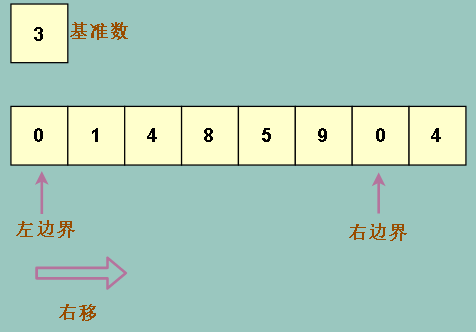
先是选取出基准数,在老师的书中将最左边的元素选作基准数,在图中,我们把基准数 3 选出来,放到数组外,表示它被一个临时变量保存

同时我们采用两个变量做为左右边界,表示当前需要操作的位置
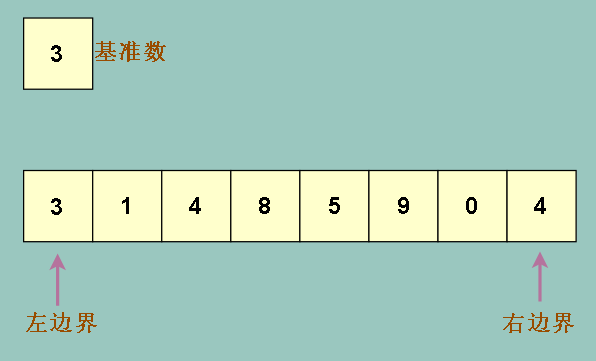
同时因为基准数就是在左边界选取的,而且基准数已经被保存了,所以我们可以大胆覆盖掉左边界位置上的元素(3)
但是要用什么覆盖呢?要分析一下我们的目的,我们想做到的是把比基准数小的元素放在基准数左边,比它的数放在右边
那么,需要覆盖的左边界的数应该是小于基准数的,那么这个数从哪来呢?从右边界来。
我们比较右边界位置的数和基准数的大小,如果右边界位置的数小于基准数,那么就让他覆盖左边界,不然的话让右边界往左移,直到找到一个小于
基准数的数,为什么要从右边界获取呢?因为我们的排序是想要从小到大排序,在右边的理应是比基准数大的数,如果右边界位置的数比基准数小
说明它的位置不对,要放到左边去,因为左边才是小的元素该待的地方
可以得出我们右边界箭头的功能 : 找到比基准数小的数
按照刚刚说的,我们比较右边界的数和基准数,右边界的数为 4,比基准数大,那么右边界左移
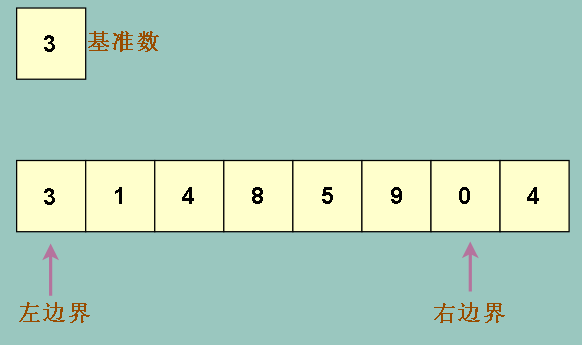
移动后再比较右边界上的数0 和基准数 3,发现右边界的数要小 ,于是我们希望右边界上的数移动到左边界去,因为左边才是小的数应该待的地方
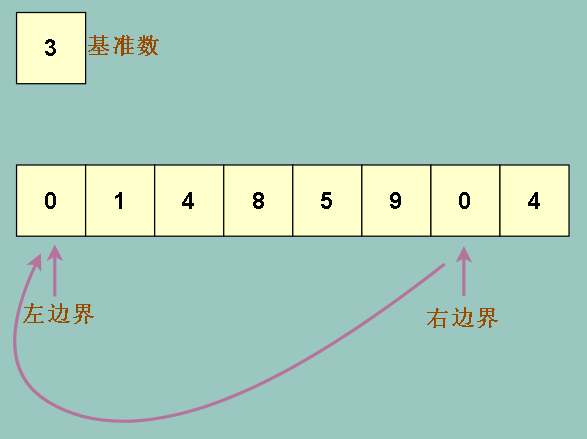
接下来怎么做呢?继续左移右边界吗?我们试试看,会发现右边界会一直左移,直到左边界上
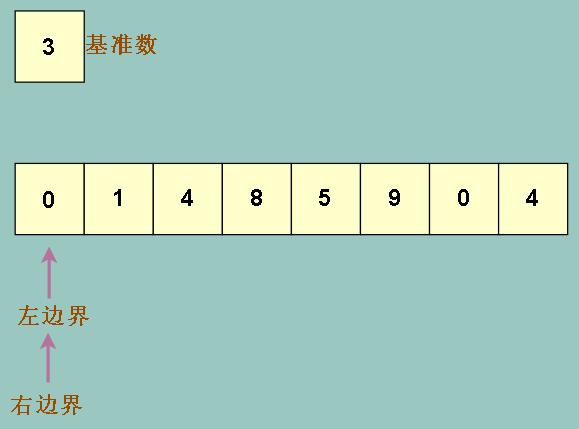
这样就会发生我们最不想看到的情况,蓝色部分是上述的比基准数大的部分,显然是错的,而且只有右边界移动而左边界不动,那么两者最终都是在
最左边相遇 (他们相遇位置就是要把基准数插入的位置),整个数组被分成 : (基准数,比基准数大的部分)
而不是 (比基准数小的部分,基准数,比基准数大的部分)
显然没有平方数组,无法达成 (log2)(n) 次操作,只有左边界右移动,右边界左移,才能尽可能地在数组中间相遇 (他们相遇位置就是要把基准数插入的位置)
这样 (比基准数小的部分,基准数,比基准数大的部分)中的 ‘比基准数小的部分’ 大小才尽可能接近 ‘比基准数大的部分’ 达成均分的效果
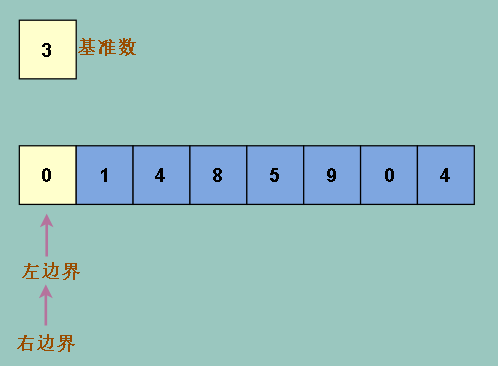
接下来我们让左边界右移,找到一个比基准数大的数为止,为什么要那么做?因为同理的,按从大到小的顺序,左边不应该出现大于基准数的数
而是应该小于基准数,如果大于,那么就把它移到右边,怎么移到右边?移到右边界位置上就可以了,因为右边界刚刚是覆盖别人位置的地方
右边界上的元素复制到了别的地方去,所以把左边界上大于基准数的数覆盖右边界上合情合理,不必担心元素丢失
如下我们找到了4 是大于基准数的元素
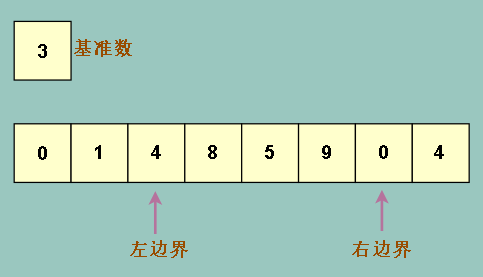
把它移动到右边界去

接下来按照循环往复的左右边界交替移动规则,现在轮到右边界左移了
因为 8 5 9 都是比基准数 3 要大的数,所以右边界一口气移道了左边界上,这时候左右边界重叠

这时候,我们把基准数 3 插入回左右边界相遇的地方,保证元素不丢失
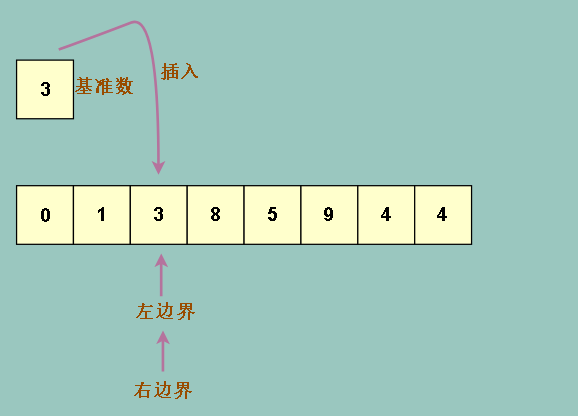
我们发现我们达成了我们想要的效果,整个数组被分成左右两部分
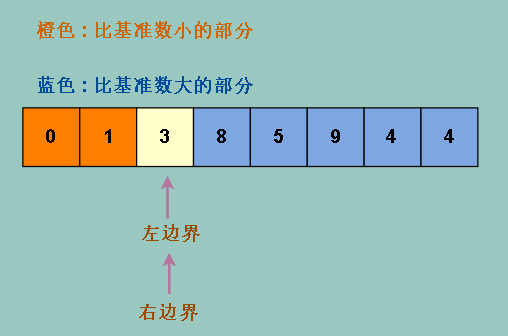
但是我们会发现,橙色部分并不等于蓝色部分,也就是我们没有把数组均分,这样并不能精确达到我们想操作 (log2) (n) 次的目的
那么,怎么样才能尽可能均分呢?我们尝试换一下分割策略,也就是用另一种方法把数组分成两半
我们打算把左边界一直往右移,直到找到一个比基准数大的元素(4)
右边界一直往左移,直到找到一个比基准数小的元素(0)
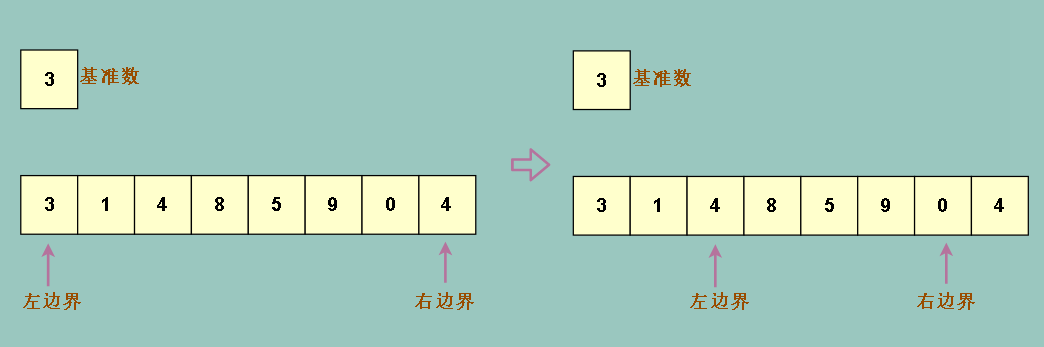
然后交换他们
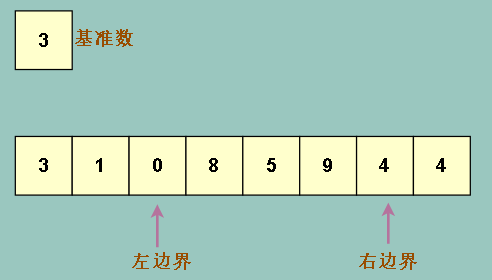
继续右移动左边界,左移右边界
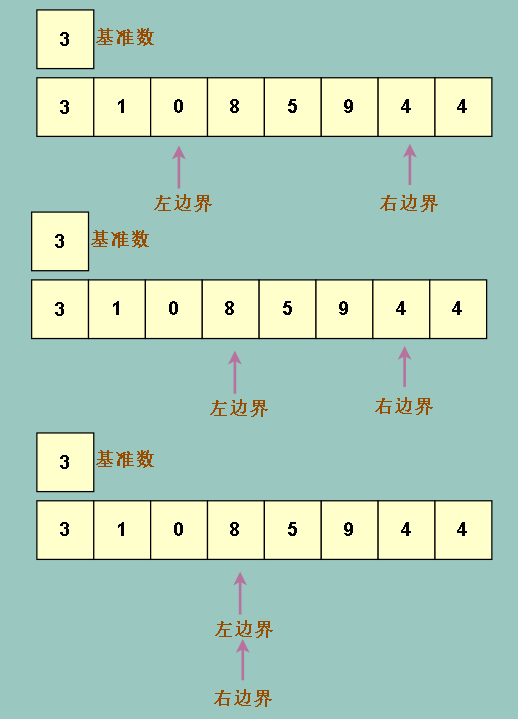
移动完之后发现两者重合了,说明这个位置左边的元素都比基准元素小,右边的都比基准元素大
因为左边界先移动,所以当前位置(左右重合位置)比基准元素大,所以我们把基准元素和当前位置左边一个位置的元素交换
也就是下图

但是我们发现,和原来一样,并没有改变分得的结果
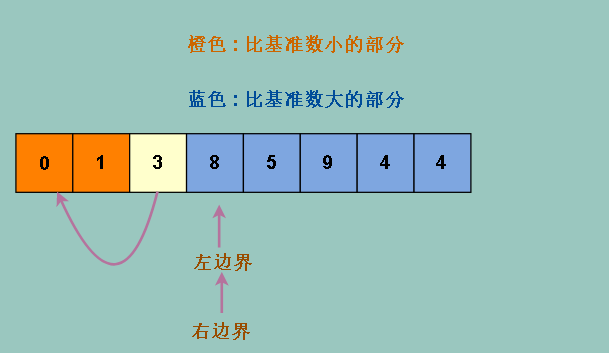
用不同的分割策略并不能达到与原来不同的效果,因为无论怎么分,最终基准数都是那个位置,他左边是比他小的数,右边是比他大的数,不会变
所以我们唯一的希望就是在基准数的选取上了,现在我们通过肉眼查找的方法,找到这组数的中位数
进行同样的操作之后,得出如下结果,其中 最右边的 4 比较特别,因为我们右边界只招小于基准数的数
可见我们的数组更接近被均分,还不够明显,我们加多一个元素 (2) , 让数组有奇数个元素,再操作一次,效果会更明显
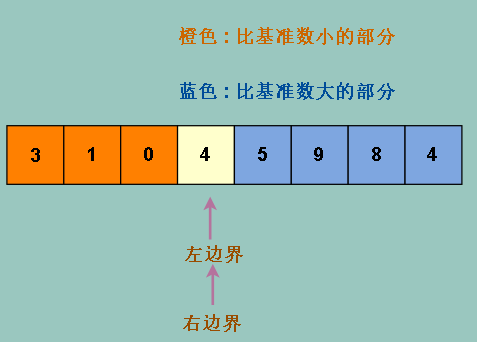
可见,如果我们选取中位数,效果更佳,因为我们选取的是中位数,而且左边的是小于中位数的部分,右边是大于中位数的部分
所以左右元素个数相等
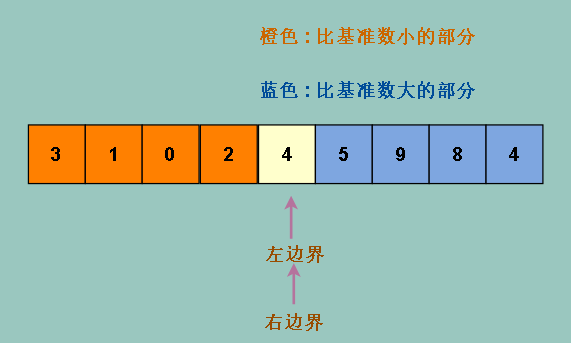
但是,虽然我们人用肉眼查找少量元素的中位数很简单,但是让机器直接找很难
而且,当数据量庞大的时候,就算是人肉眼也很难找到中位数,几乎不可能,机器如果要找到,则要经过大量的遍历,得到中位数的位置
那么,我们想让基准数尽可能贴近中位数,而寻找基准数可能的策略是 :
1.第一个元素做为基准数
2.随机寻找
3.将某个特定位置的元素当作基准数
一般情况下,需要我们排序的数组,是一组随机数,用上述 3 种方法似乎都是获得一个随机的数,没有什么区别
而方法 2 需要我们使用某种随机机构,比如 Java 的 Random 类 来生成随机位置的下标,这种做法会消耗不少时间
方法 1 在某些极端条件下,会让我们的排序时间变得漫长而糟糕
比如全顺序和全逆序
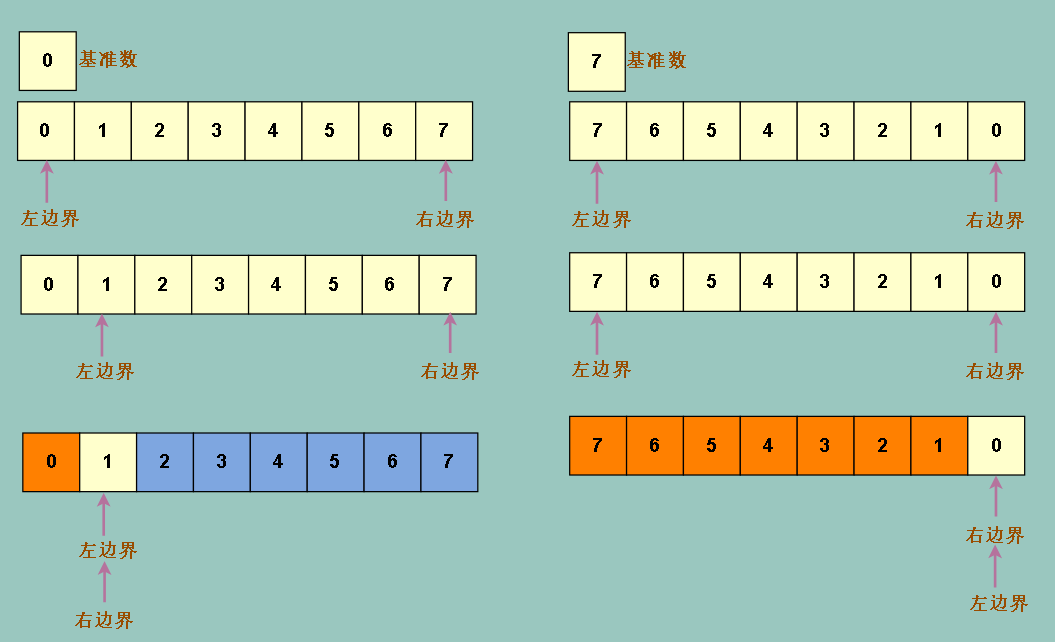
左右分配极端不均衡
那么,还剩方法3
虽然方法 3 也不是完全可靠的方法,但是在极端条件下,它会比其他选法更加高效
还要考虑一种特殊情况,如果我们的数组里的值,全部是相等的,怎么办?
我们会发现我们左边界先冲的话,一开冲就冲到底,因为沿途没有比基准数大的数
如果右边界开冲,同样会一冲冲到尽头,因为沿途没有小于基准数的数
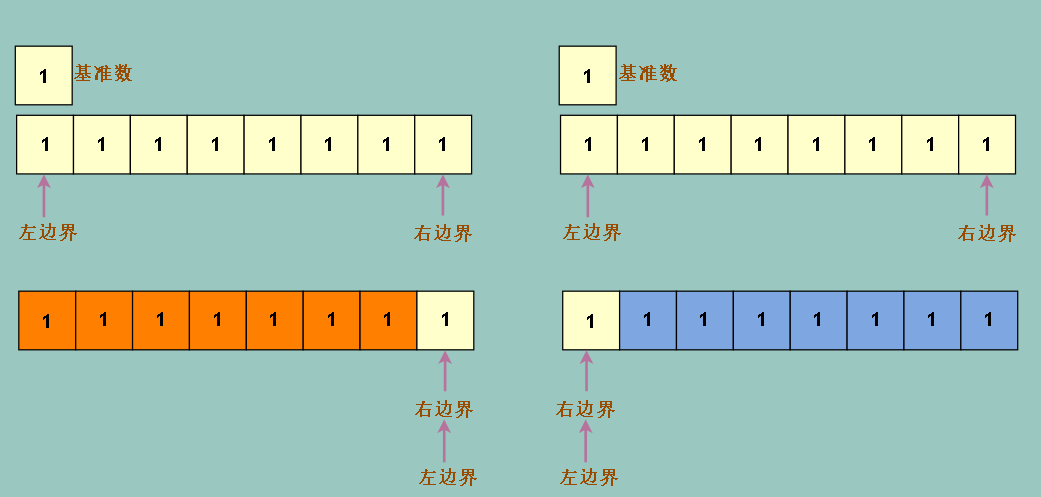
冲到底的代价是我们要进行和数组个数同样多次的线性操作,时间复杂度 n * n = n ^ 2

我们的快速排序退化成和冒泡排序一样慢,所以有一个问题,遇到和基准数相同的元素时,边界该不该停下来?
显然是要停下来的 ,如果这样的话,左边界的作用变成了找到大于等于基准数的元素 右边界的作用变成了找到小于等于基准数的元素
针对上述极端的全部元素相等条件,左右边界会各自移动一个脚步后交换元素
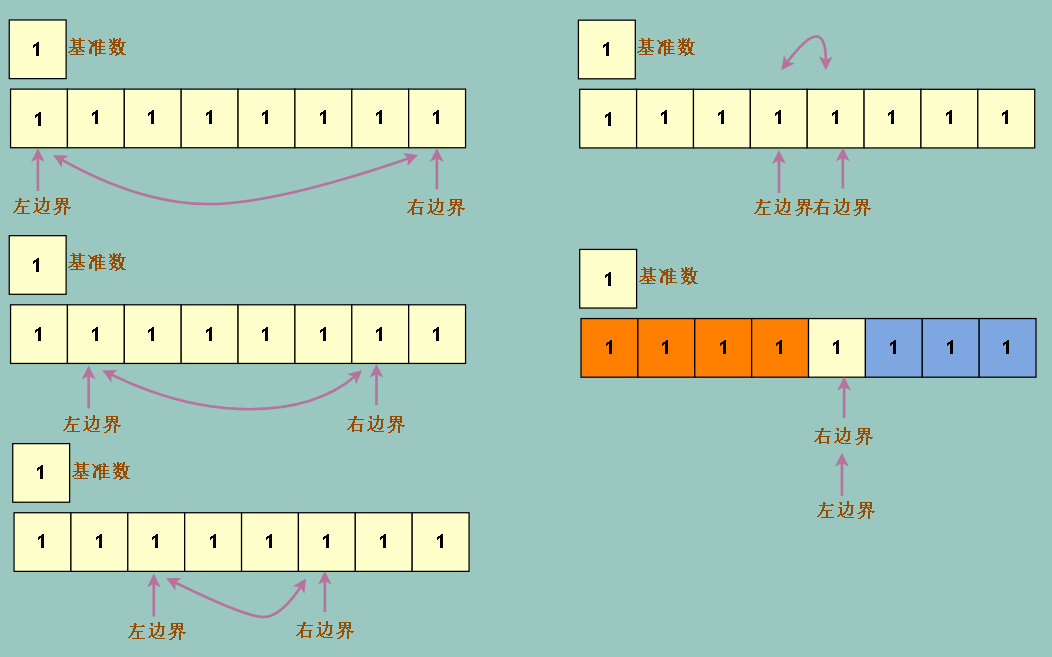
这样得出的结果才接近均分整个数组,提高了我们排序的普适性
于是,我们得出我们的结论 :
1.基准数应该从数组中间选取
2.调整分割策略,当左右边界遇到和基准数相同元素时,需要停下移动
调整后的分割策略中,用伪代码表示一下左右边界的移动情况
假设变量 l 是左边界,r 是右边界, 待排序数组是 arr, 基准数是pivot
那么伪代码 :
int l,r,pivot; while(arr[l] < pivot){ l ++; } while(arr[r] > pivot){ r ++; }
第一个while表示如果左边界上的数小于基准数(合理)就让左边界右移,直到达到不合理的地方(左边界大于等于基准数的地方)
第二个while同理
如果左右移动完之后就交换两者,注意要保证 l 和 r 的合法位置,也就是左边界 l 要小于右边界 r ,左边界在右边界左边
int l,r,pivot; while(arr[l] < pivot){ l ++; } while(arr[r] > pivot){ r --; } if(l < r){ swap(arr, l, r); }
但是,仔细的你可能会发现,l 和 r 移动过程中可能超出数组边界,导致 IndexOutOfArrayBound 之类的错误
所以,我们要判断 l,r,让他们不出界
int l,r,pivot; while(l < arr.length && arr[l] < pivot){ l ++; } while(r >= 0 && arr[r] > pivot){ r --; } if(l < r){ swap(arr, l, r); }
但是,要记住,这里的两个while是对数组的线性操作,也是我们的主操作,也就是之前一直提到的,如果我们操作次数是 (log2)(n) 次,那么总时间复杂度就是
次数乘以我们这种线性操作的耗时 n = ((log2)(n)) * n = n * (log2)(n) ,也就是 O(n * logn)级别
显然,这两个while是我们的主操作,我们不想让它变得复杂,不想加上判断边界这种对于我们排序实际上没什么意义的操作
那么按照我们左右边界移动的条件,也就是左边界遇到大于等于基准数的元素后停止 右边界遇到小于等于基准数的元素停止
那么如果我们的最左边下标的元素小于等于基准数,不就可以让右边界左移的过程中不超出下标范围了?
如果我们在数组的最右边,放一个大于等于基准数的元素,不就可以防止左边界右移过程中超出范围了?
我们暂且称这两个数为 左栅 和 右栅
数组的中间是选出基准数的,所以我们从其他位置随机选取两个数来充当上述的 左栅 和 右栅
但是之前说过,我们排序的数组一般是随机的,所以我们在哪个位置选取数都有随机性
所以我们选取第一个元素和最后一个元素,于是我们有了三个数 : 左栅 右栅 和基准数
但这三个数只是临时的,因为他们的大小关系不确定(因为原数组无序),我们需要将他们比较之后,把最小者当作左栅,最大者当作右栅,剩下一个就是 基 准数了
假设我们获得基准数的方法是getPivot
伪代码则如下 :
其中 leftBound 是待排序数组的最左边,也就是左边界一开始没移动前的下标,rightBound是待排序数组的最右边,也就是右边界一开始没移动前的下标
int getPivot(int[] arr, int leftBound, int rightBound){ int mid = (leftBound + rightBound) / 2; if(arr[leftBound] > arr[mid]){ // 小的放左边 swap(arr, leftBound, mid); } if(arr[rightBound] < arr[leftBound]){ //更小的放左边 swap(arr, rightBound, leftBound); } if(arr[rightBound] < arr[mid]){ swap(arr, rightBound, mid); //leftBound 已经是最小的了 只用把中间和右边大的那个放在右边 } return arr[ mid ]; }
这样,我们的某个数组中各个要素的位置关系 :

因为左栅已经是小于基准数的元素,而右栅已经是大于基准数的元素,所以我们把左边界从左栅右边的一个位置开始,
右边界从右栅的左边一个位置开始
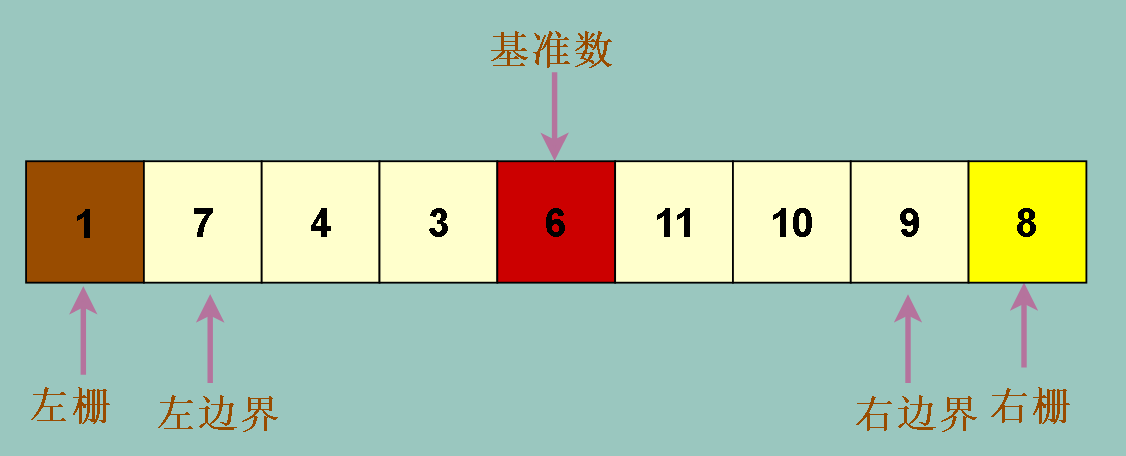
但是我们发现,如果我们把基准数放在数组中间,则在左右边界交换过程中,基准数会被移来移去,我们无法直到最终基准数在哪
除非编写多几条语句嗅探左边界或右边界操作基准数,记录操作后基准数的去向,显然我们不想那么做。
比如下面这一组数组

选取要素后 :

进行排序 :

显然我们不想让我们的主操作变得复杂,我们想让他越简单越好,所以我们可以直接把基准数放在右栅的左边一个位置
而让右边界从基准数左边一个位置开始向左移动。左边界遇到大于等于基准数的元素会停下来,基准数也可以用来拦住左边界右移
于是我们让中间的基准数和 right - 1 位置的数换一下,让右边界左移一个位置
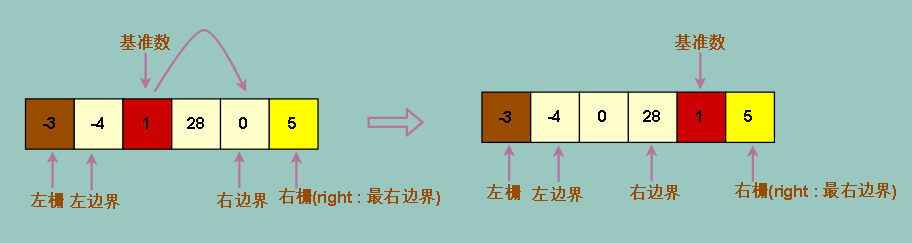
完善我们的代码
获得基准数的部分新增两句 :
swap(arr, mid, right = right - 1); // 把基准数放在 right - 1 位置 也就是右栅左边一个位置
return arr[right]; // 返回基准数
int getPivot(int[] arr, int leftBound, int rightBound){ int mid = (leftBound + rightBound) / 2; if(arr[leftBound] > arr[mid]){ // 小的放左边 swap(arr, leftBound, mid); } if(arr[rightBound] < arr[leftBound]){ //更小的放左边 swap(arr, rightBound, leftBound); } if(arr[rightBound] < arr[mid]){ swap(arr, rightBound, mid); //leftBound 已经是最小的了 只用把中间和右边大的那个放在右边 } swap(arr, mid, rightBound = rightBound - 1); // 把基准数放在 right - 1 位置 也就是右栅左边一个位置 , 反正rightBound是基础
类型形参对他操作不影响外部,免得在下面再算一次 rightBound - 1 return arr[rightBound]; // 返回基准数 }
排序主体部分 :
void quickSort(int[] arr, int left, int right){ int l = left + 1,r = right - 2,pivot = getPivot(arr, left, right); while(arr[l] < pivot){ l ++; } while(arr[r] > pivot){ r --; } if(l < r){ swap(arr, l, r); } }
如果排序主体只是那么写的话,我们会发现交换一次后,左右边界就不动了
所以要加一个死循环让他们继续移动,跳出死循环的条件是 左边界 l 越到了或越过了 右边界 r
void quickSort(int[] arr, int left, int right){ int l = left + 1,r = right - 2,pivot = getPivot(arr, left, right); while(true){ while(arr[l] < pivot){ l ++; } while(arr[r] > pivot){ r --; } if(l < r){ swap(arr, l, r); }else{ break;
}
} }
但实际上,如果我们的 l 和 r 恰巧都移动到了两个和基准数一样的数上,会有什么效果呢?
就如下图,左边界 l 探测到当前元素是大于等于基准数的
右边界 r 探测到当前元素是小于等于基准数的
两者都会跳出自己的while循环,不会各自加一,而且 l < r 所以交换
接着又从当前位置开始,继续判断,又直接跳出while循环,又交换,循环往复,形成死循环
所以我们要把加一的操作放在外面,加一后(移动后)才判断当前左或右边界位置是否满足条件

void quickSort(int[] arr, int left, int right){ int l = left + 1,r = right - 2,pivot = getPivot(arr, left, right); while(true){ while(arr[++ l] < pivot){} // 加1操作提前 while(arr[-- r] > pivot){} // 减1操作提前 if(l < r){ swap(arr, l, r); }else{ break; } } }
但是我们的 l 要从left + 1开始, r要从right - 2 开始
如果 l 一开始就要 ++, r 一开始就要 --,那么 l 的初值要改成 left,才能从 left + 1 位置开始判断
r 的初值要从 right - 1 开始,才能从 right - 2 开始判断
完善我们的代码 :
void quickSort(int[] arr, int left, int right){ int l = left,r = right - 1,pivot = getPivot(arr, left, right); while(true){ while(arr[++ l] < pivot){} // 加1操作提前 while(arr[-- r] > pivot){} // 减1操作提前 if(l < r){ swap(arr, l, r); }else{ break; } } }
l 和 r 相遇时候,因为是 l 先移动,所以相遇处一定比基准数大
所以我们可以把该处和处于 right - 1 位置的基准数调换
完善代码:
void quickSort(int[] arr, int left, int right){
int l = left,r = right - 1,pivot = getPivot(arr, left, right);
while(true){
while(arr[++ l] < pivot){} // 加1操作提前
while(arr[-- r] > pivot){} // 减1操作提前
if(l < r){
swap(arr, l, r);
}else{
break;
}
}
swap(arr, l, right - 1);
}
接着要添加递归调用
void quickSort(int[] arr, int left, int right){ int l = left,r = right - 1,pivot = getPivot(arr, left, right); while(true){ while(arr[++ l] < pivot){} // 加1操作提前 while(arr[-- r] > pivot){} // 减1操作提前 if(l < r){ swap(arr, l, r); }else{ break; } } swap(arr, l, right - 1); quickSorted(arr, left, l - 1); quickSorted(arr, l + 1, right); }
但还有一个点,我们要有至少三个元素,也就是说 right - left > 1
当数组规模较小时候,快速排序往往不如某些时间复杂度相对较高的排序算法
这一概念在Mark Allen Weiss 的 Data Structures and Algorithm Analysis in C 中提到
时间将缩减 15 % 左右
经过测试,对一亿条无序数据排序
如果在问题规模小于等于19的时候使用插入排序,耗时大概在
76秒左右
如果小于等于3的时候使用插入排序,耗时大概在
83秒左右
经过不同最小数组下限大小的测试,确实发现可以提高效率,这一点还有待研究。
具体的耗时和使用直接插入排序的问题下限规模的部分数据图像如下图所示
另附上电脑环境

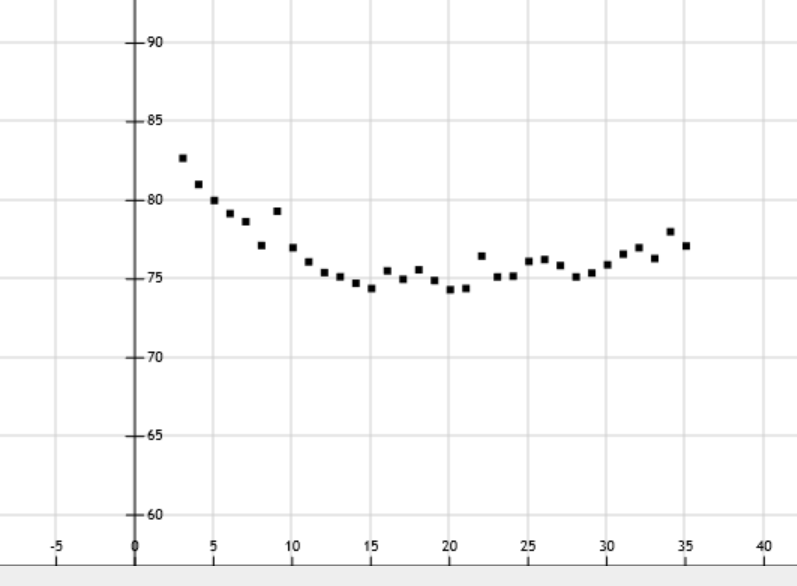
可见,小数组 范围内,确实效率有所提高
以后有待做更多测试验证
完善代码 :
void quickSort(int[] arr, int left, int right, int threshold){
if(right - left > threshold){
int l = left,r = right - 1,pivot = getPivot(arr, left, right);
while(true){
while(arr[++ l] < pivot){} // 加1操作提前
while(arr[-- r] > pivot){} // 减1操作提前
if(l < r){
swap(arr, l, r);
}else{
break;
}
}
swap(arr, l, right - 1);
quickSorted(arr, left, l - 1);
quickSorted(arr, l + 1, right);
}else{
insertSort(arr, 0, arr.length - 1)
}
}
现在我们来分析下时间复杂度:
根据程序,我们的时间主要消耗在三个部分

又是我们喜闻乐见的递归式
假设 l - left = p
T(N) = 分割时间 + T(p) + T(N - p - 1)
分割时间就是 第一个大框 while 循环用的时间
T(p) 是第二个框使用的时间
T(N - p - 1)是第三个框使用的时间
因为分割操作时线性地扫描数组,所以它应该是一个 k * N 级别的时间
于是上述式子等价于
T(N) = k * N+ T(p) + T(N - p)
如果我们的 p = N - p, 也就是 p 每次都是数组中间的位置,每次我们都能均分数组,也就是每次的基准数都是中位数
那么 T(N) = k*N + 2T(N/2)
类似上一章我讲过的归并排序,可以推出 T(N) = N * (log)(N)
这是极好情况下
如果是极坏情况下,也就是我们的数组被分成基准数一组,其他数一组
也就是这种情况

T(p) = 1, p是一个基准数的规模,就是1
T(N) = 1 + T(N - 1) + k *N
我们对两边除以 N
T(N) / N = 1 / N + T(N - 1) / N + k
忽略掉 1
T(N) = T(N - 1) + k * N
把部分公式列出:
T(N) = T(N - 1) + k * N
T(N - 1) = T(N - 2) + k * (N - 1)
T(N - 2) = T(N - 3) + k * (N - 2)
T(N - 3) = T(N - 4) + k * (N - 3)
...
T(2) = T(1) + k * (2)
T(1) = T(0) + k * (1)
喜闻乐见地发现又可以消去,得到:
T(N) = T(0) + k * Sum(1 , N)
取T(0) = 1, 并且忽略掉,则 T(N) = k * Sum(1 , N) = k * N * (1 + N) / 2
当 N 取无穷大,结果还是 O (N^2) 级的
然而我们更希望看到的是平均时间复杂度 :
假如我们的 p 的大小从 1 到 N , 那么我们可以求一下 T(p) 的平均值
也就是T(p) = (1 / N) Sum(i = 1, N) T(i)
因为 T(N) = k * N+ T(p) + T(N - p) 中的 N - p 和 p 是互补为 N 的关系
所以我们可以认为 T(p) 和 T(N - p) 的时间接近,于是我们把 T(p) 的平均值代入公式
T(N) = 2 * [ (1 / N) Sum(i = 1, N) T(i) ] + k * N
来求T(N)的平均值
两边乘以 N 有助于让我们把求和消掉
T(N) * N = 2 * [ Sum(i = 1, N) T(i) ] + k * N ^ 2
利用求和的特性,留下一个 i = N 时的 T(i)
T(N - 1) * (N - 1) = 2 * [ Sum(i = 1, N - 1) T(i) ] + k * (N - 1) ^ 2
Sum(i = 1, N) T(i) - Sum(i = 1, N - 1) T(i) = T(N)
也就是 T(N) * N - T(N - 1) * (N - 1) = 2 * T(N) + k * ( N ^ 2 - (N - 1) ^ 2)
T(N) * N = (N + 1) * T(N - 1) + 2*k*N - k
去掉 k
T(N) * N = (N + 1) * T(N - 1) + 2*k*N
观察一下,好像又是对称的公式,可以进行消去
两边除以 (N + 1) * N
T(N) / (N + 1) = T(N - 1) / N + 2 * k / (N + 1)
假设 An = T(N) / (N + 1)
那么
An = A(n - 1) + 2 * k / (N + 1)
A(n - 1) = A(n - 2) + 2 * k / (N)
A(n - 2) = A(n - 3) + 2 * k / (N - 1)
...
A(2) = A(1) + 2 * k / (3)
A(1) = A(0) + 2 * k / (2)
左右分别各自加和,最后消去得出 An = A(0) + 2 * k * Sum(2, N + 1) = T(0) / 1 + 2 * k * Sum(1/2, 1/(N + 1)) = 1 + 2 * k * Sum(1/2, 1/(N + 1))
约等于 2 * k * Sum(1/2, 1/(N + 1))
这个求和查了一下作业帮

最后结果大概是 ln( n ) 级别
也就是指数级别
于是 An = T(N) / (N + 1) = ln (N) 那么 T(N) = (N) * ln(N)
时间复杂度为 O(N * log N)
呼,写了一天累死了,中途博客园还吞了我的内容,白写了一早上。溜了溜了。
还有一点略坑的地方
就是对数组两位置元素进行交换
这是我一开始的写法,后来发现无缘无故数组里多了0
private void swap(int[] arr, int indexA, int indexB){ arr[indexA] = arr[indexA] ^ arr[indexB]; arr[indexB] = arr[indexA] ^ arr[indexB]; arr[indexA] = arr[indexA] ^ arr[indexB]; }
后来检查如果 indexA 和 indexB 相同,最终两个数会为0
因为两个数其实就是同一个内存空间的数据
就像 A = A ^ A
这时候 A 一定等于 0
A = A ^ A 不还是 0 吗...
所以下标相等的时候不用交换了,直接退出就好了
private void swap(int[] arr, int indexA, int indexB){ if (indexA == indexB) { return; } arr[indexA] = arr[indexA] ^ arr[indexB]; arr[indexB] = arr[indexA] ^ arr[indexB]; arr[indexA] = arr[indexA] ^ arr[indexB]; }