-
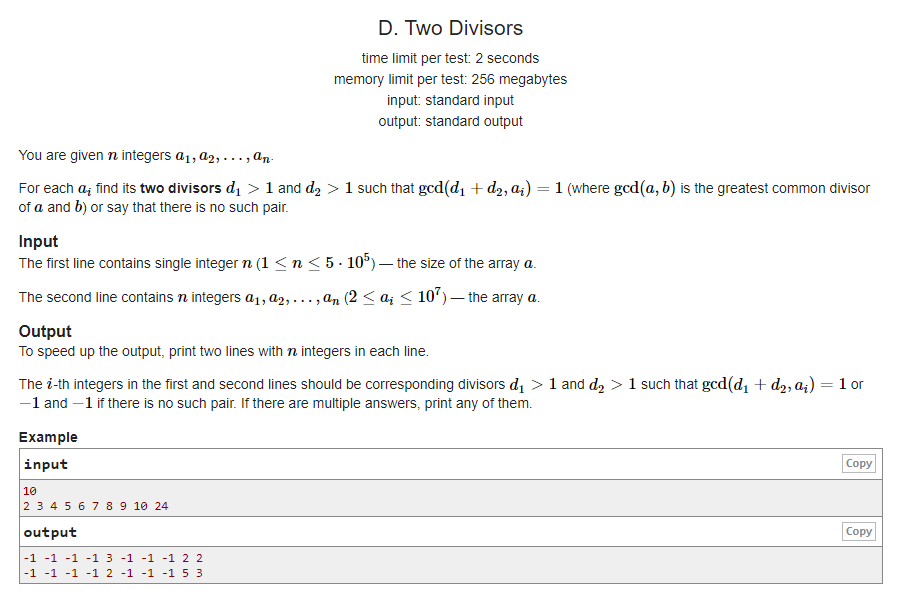
题意:有\(n\)组数,对于每组数,问是否能找到两个因子\(d_{1},d{2}\),使得\(gcd(d_{1}+d_{2},a_{i}=1)\),如果有,输出它们,否则输出\(-1\).
-
题解:对于这题,首先我们要推两个gcd的公式:
1) $gcd(a,b)=gcd(a+b,b) $.
2) 若\(gcd(a,c)=1 \ => gcd(a,bc)=gcd(a,b)\).
这两个公式应该都很容易证明.
因此我们推出:若\(gcd(x,y)=1\),则:\(gcd(x+y,xy)=1\).
所以我们就可以对\(a_{i}\)质因数分解,得到:\(p_{1}^{k1},p_{2}^{k2}.....p_{n}^{kn}\).
我们令\(d_{1}=p_{1}^{k1}\),\(d_{2}=\frac{a_{i}}{d_{1}}\)即可.
下面给出公式的证明过程:

-
代码: (用到了欧拉线性筛)
#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <algorithm> #include <stack> #include <queue> #include <vector> #include <map> #include <set> #include <unordered_set> #include <unordered_map> #define ll long long #define fi first #define se second #define pb push_back #define me memset const int N = 1e7 + 10; const int mod = 1e9 + 7; const int INF = 0x3f3f3f3f; using namespace std; typedef pair<int,int> PII; typedef pair<ll,ll> PLL; int n; int prime[N]; int cnt; bool st[N]; int a[N]; vector<int> v; vector<PII> ans; void get_prime(){ for(int i=2;i<=N;++i){ if(!st[i]) prime[++cnt]=i; for(int j=1;j<=cnt && prime[j]<=n/i;++j){ st[i*prime[j]]=true; if(i%prime[j]==0) break; } } } void divide(int x){ int tmp=x; for(int i=1;i<=cnt;++i){ if((ll)prime[i]*(ll)prime[i]>(ll)x) break; if(x%prime[i]==0){ int t=1; while(x%prime[i]==0){ x/=prime[i]; t*=prime[i]; } v.pb(t); } } if(x>1) v.pb(x); if(v.size()<2) ans.pb({-1,-1}); else ans.pb({v[0],tmp/v[0]}); v.clear(); } int main() { ios::sync_with_stdio(false);cin.tie(0); cin>>n; for(int i=1;i<=n;++i){ cin>>a[i]; } get_prime(); for(int i=1;i<=n;++i){ divide(a[i]); } for(auto w:ans) printf("%d ",w.fi); printf("\n"); for(auto w:ans) printf("%d ",w.se); return 0; }