卷积——五分钟了解"

了解卷积

在先前的文章中，我们建立了对卷积神经网络的理解，而没有涉及任何重要的数学。然而，要走得更远，我们需要了解卷积。

如果我们只是想了解卷积神经网络，那么大概了解卷积就足够了。但是，本系列文章的目的是将我们带到卷积神经网络的前沿，并探索新的选择。为此，我们需要非常深入地了解卷积。

值得庆幸的是，通过一些示例，卷积成为一个非常简单的想法。（刚看到作者这句话，我觉得他在扯淡，但下面的一分钟，我就彻底明白了卷积是在干什么，太强啦）

掉落小球的启示

想象一下，我们将一个球从某个高度掉落到地面上，假设在该地面上该小球将只向一个方向运动（下面的图例是向右）。如果您将球抛下然后从其着陆点上方再次抛下，它走出距离为 c 的可能性有多大？

让我们来分解一下这个过程。在第一次下降之后，它将以概率 f(a) 从起点降落 a 个单位，其中 f 是概率分布。

现在，在第一次下降之后，我们将球捡起并将其从第一次停下的点上方的另一个高度下降。小球滚到偏离新起点 b 个单位的概率为 g(b)，如果小球从不同的高度掉落，则该小球滚到偏离新起点 b 个单位的概率 g 可能是不同的概率分布。

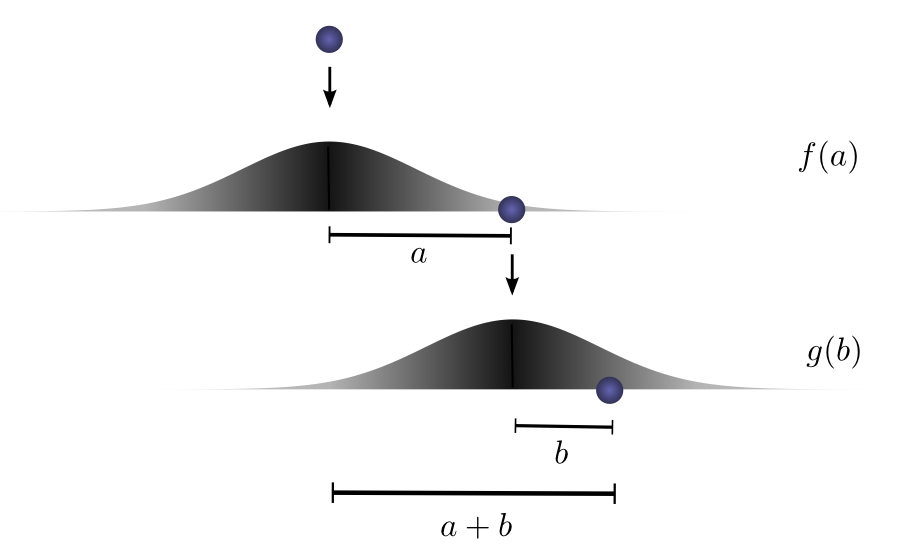
如果我们确定第一个落点的结果，也就是说我们知道球会走距离 a ，对于总距离为 c 的球，第二个落点的行进距离也就固定了，我们假设第二次下落后的行进距离为 b ，其中 a + b = c 。因此发生这种情况的可能性就是 f(a) * g(b) （这儿的意思是 在这两次小球下落中，发生如下结果"总距离为 c ,第一次距离为 a , 第二次距离为 b "的概率为 f(a) * g(b) ）

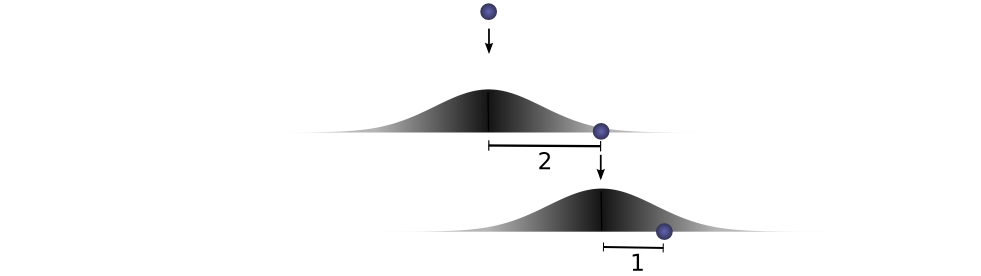
让我们考虑一个具体的离散示例。我们希望总距离 c 为3。如果第一次滚动，a = 2 ，则第二次必须滚动 b = 1 才能达到我们的总距离 a + b = 3 ，其概率为 f(2) * g(1) 。

但是，这不是我们达到总距离为 3 的唯一方法。小球第一次也可以滚动1个单位，而第二次滚动2个单位。或第一次为0，第二次为3。只要加到3，它就可以取任何 a 和 b 。

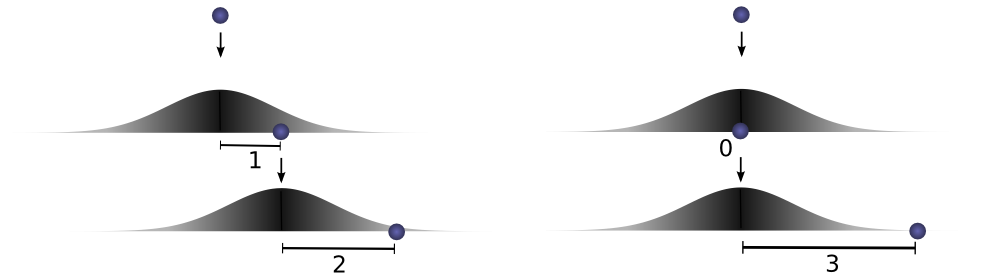
概率分别为 f(1) ⋅ g(2) 和 f(0) ⋅ g(3) 。

为了找出小球到达总距离 c 的总可能性，我们不能仅考虑一种到达 c 的可能方式。相反，我们考虑将 c 分为两个下落后举例为 a 和 b 的所有可能方法，并对每种方法的概率求和。

... f(0) ⋅ g(3) + f(1) ⋅ g(2) + f(2) ⋅ g(1) ...

我们已经知道，每种情况a + b = c 的概率就是 f(a) ⋅ g(b) 。因此，对a + b = c的每个解求和，我们可以将总似然表示为：

[sum_{a+b=c}{f(a) ⋅ g(b)} ]

事实证明，我们正在做卷积！特别地，定义在 c 处的 f 和 g 的卷积定义为：

[(f * g)(c) = sum_{a+b=c}{f(a) ⋅ g(b)} ]

如果将 b = c - a 替换为：

[(f * g)(c) = sum_{a+b=c}{f(a) ⋅ g(c-a)} ]

这就是卷积的标准定义。（没骗你吧，五分钟绝对看懂。）

为了更具体一点，我们可以考虑小球可能着陆的位置。在第一次下降之后，它将以概率 f(a) 停在中间某个位置 a 。如果它降落在 a 上，则它有 g(c-a) 个降落在位置 c 上的概率。

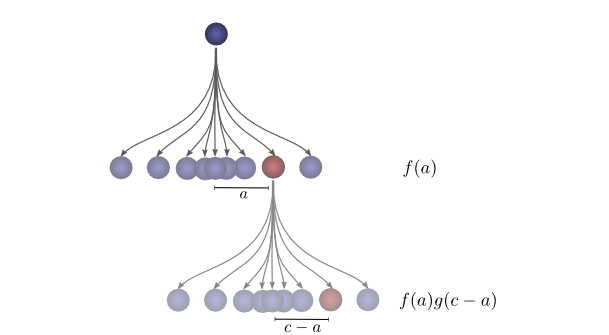
为了得到卷积，我们考虑所有某个中间位置。

可视化卷积

有一个很好的技巧，可以帮助人们更轻松地思考卷积。

首先，观察。假设一个小球从其起点降落一定距离 x 的概率为f(x) 。然后，此后它从着陆点开始距离 x 的概率为f(-x)。

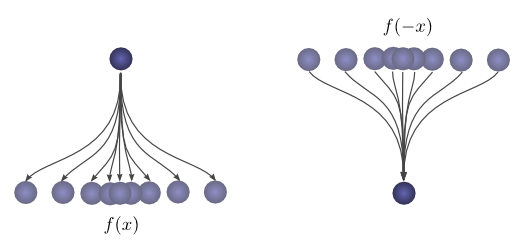
如果我们知道小球在第二次掉落后落在 c 位置，那么第一次下落停下的位置是 a 的概率是多少？

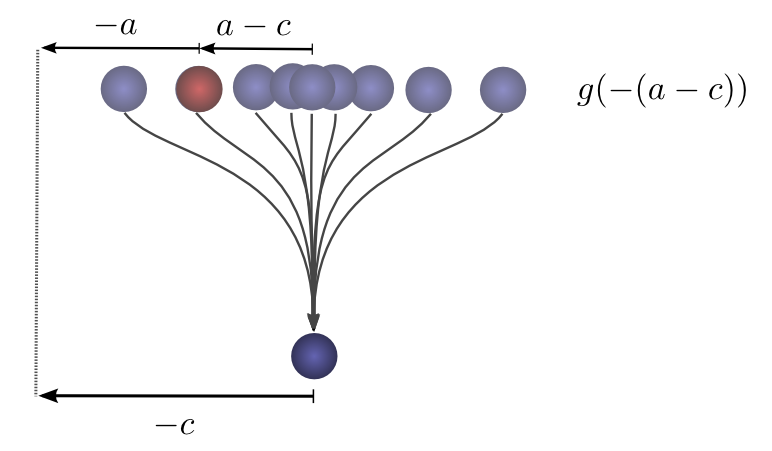
因此，第一次下落停下的位置是 a 的概率为 g( -(a-c) ) = g(c-a) 。

现在，考虑每个中间位置对最终落入 c 的球的贡献率。我们知道第一次下降小球行进到中间位置 a 的概率是f(a) 。我们还知道，小球已经出现在 a 上，然后它第二次降落在 c 上的概率为 g(c-a) 。

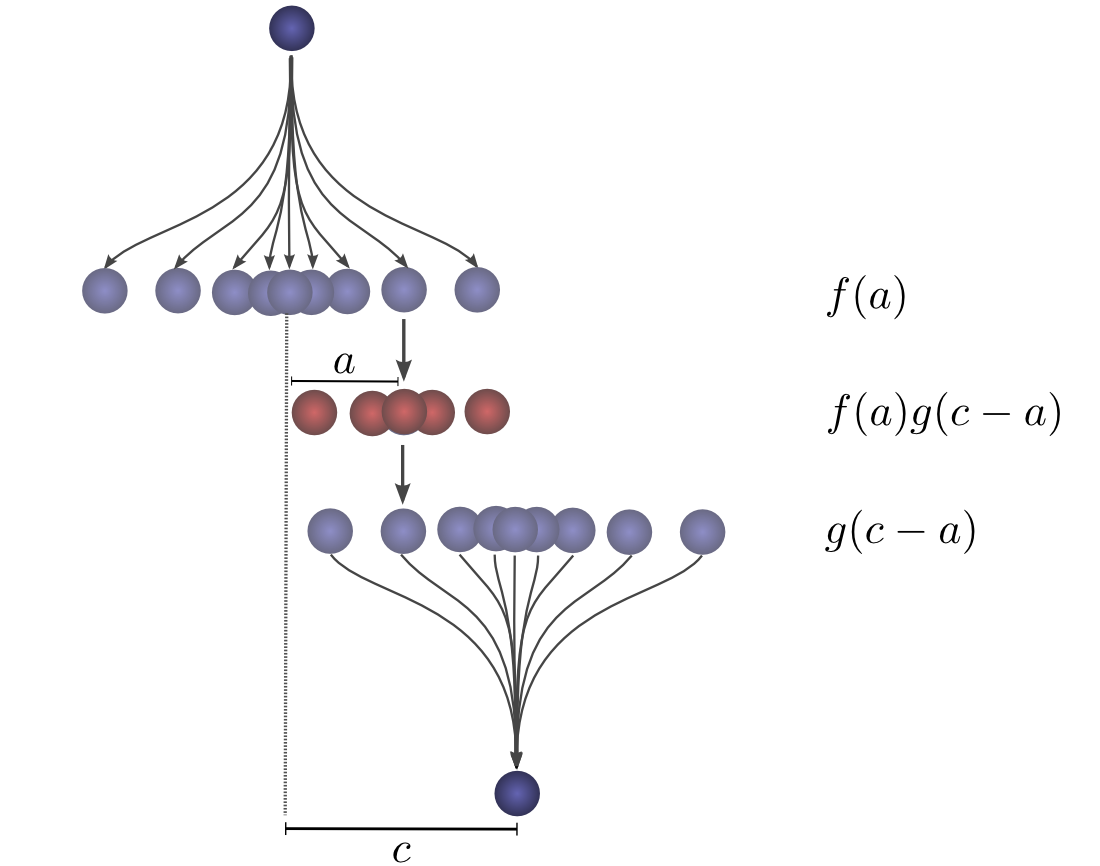
对上述求和，我们就得到了卷积。

这种可视化方法的优势在于，它使我们可以得到单个图片中以 c 值可视化卷积的评测。通过移动下半部分，我们可以评估其他 c 值的卷积。这使我们能够从整体上理解卷积。

例如，我们可以看到它在分布对齐时达到峰值。

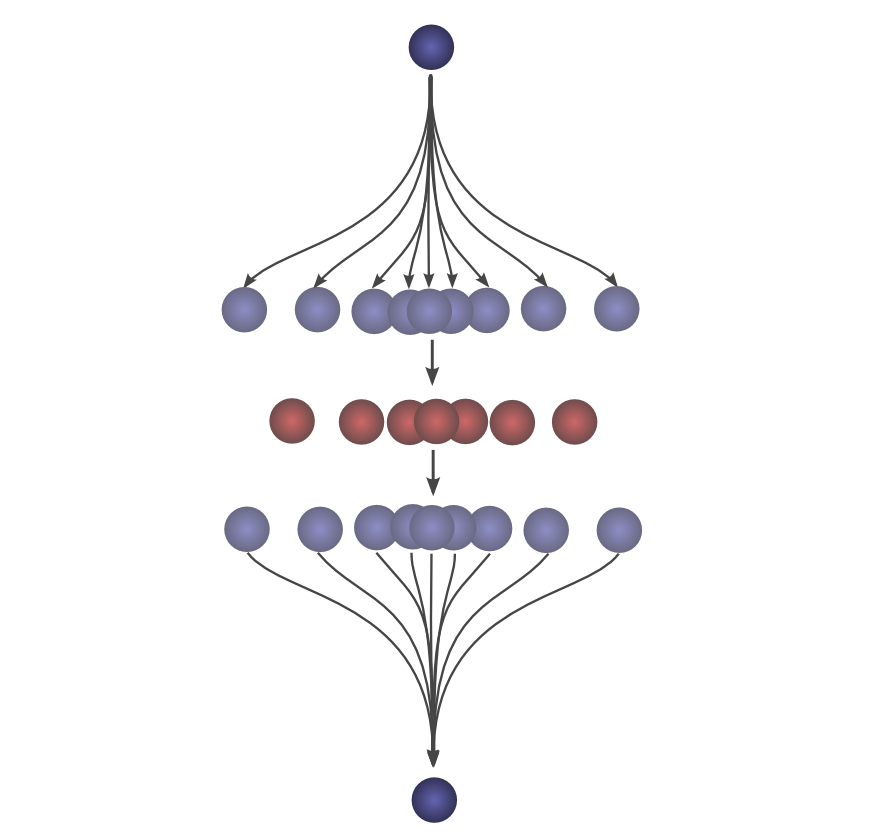
并且随着分布之间的交点变小而缩小。

通过在动画中使用此技巧，可以从视觉上理解卷积。

在下面，我们可以看到两个框函数的卷积：

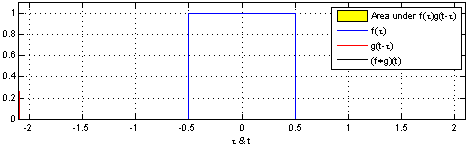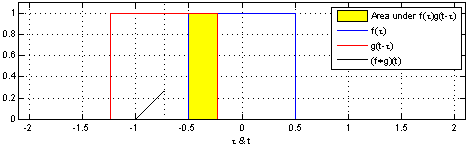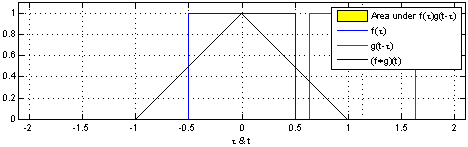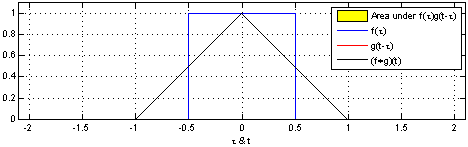
​ From Wikipedia

有了这种观点，很多事情就会变得更加直观。

让我们考虑一个非概率示例。卷积有时在音频处理中使用。例如，一个函数可能会使用其中有两个尖峰但在其他所有地方为零的函数来创建回波。当我们的双尖峰功能滑动时，一个尖峰首先击中一个时间点，将该信号添加到输出声音中，然后又出现另一个尖峰，并添加第二个延迟副本。

高维卷积

卷积是一个非常通用的想法。我们还可以将它们用于更大的维度。

让我们再次考虑一个落球的例子。现在，随着它的下落，它的位置不仅在一维，而且在二维。

卷积与以前相同：

[(f * g)(c) = sum_{a+b=c}{f(a) ⋅ g(b)} ]

只是现在，a，b 和 c 是向量。更明确地说，

[(f * g)(c_1,c_2) = sum_{a_1+b_1=c_1 , a_2+b_2=c_2}{f(a_1,a_2) ⋅ g(b_1,b_2)} ]

或在标准定义中：

[(f * g)(c_1,c_2) = sum_{a_1+b_1=c_1 , a_2+b_2=c_2}{f(a_1,a_2) ⋅ g(c_1-b_1,c_2-b_2)} ]

就像一维卷积一样，我们可以将二维卷积视为将一个函数滑动到另一个函数之上，相乘和相加。

一种常见的应用是图像处理。我们可以将图像视为二维函数。许多重要的图像转换都是卷积，您可以在其中将图像函数与一个非常小的局部函数（称为“内核”）进行卷积。

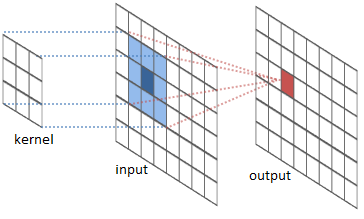
内核滑动到图像的每个位置，并计算一个新像素作为其浮动像素的加权和。

例如，通过平均3x3像素盒，我们可以使图像模糊。为此，我们的内核对框中的每个像素取值1/9，

我们还可以通过在两个相邻像素上取值-1和1来检测边缘，而在其他所有位置取零。也就是说，我们减去两个相邻像素。当并排像素相似时，这大约等于零。但是，在边缘上，相邻像素在垂直于边缘的方向上有很大不同。

卷积神经网络

那么，卷积与卷积神经网络有何关系？考虑一个具有输入{xn} 和输出 {yn}的一维卷积层，就像我们在上一篇文章中讨论的那样：

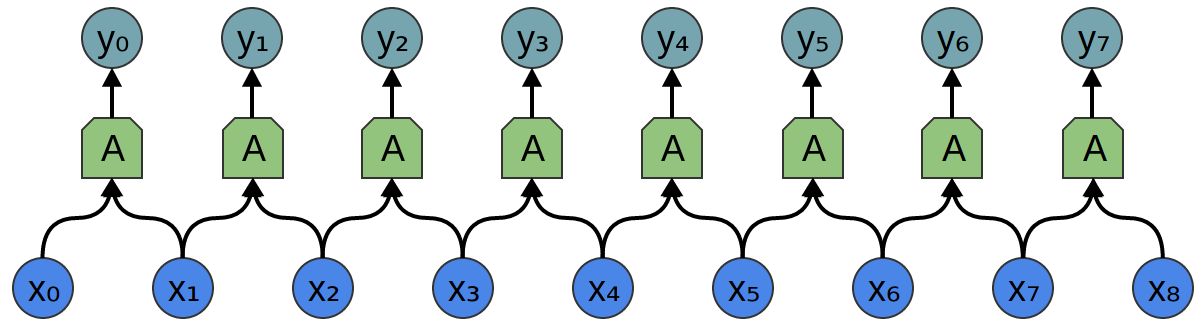
正如我们观察到的，我们可以用输入来描述输出：

[y_n=A(x_n,x_{n+1},...) ]

通常，A 是多个神经元。但是，我们先假设它只是一个神经元一小会儿。回想一下，神经网络中的典型神经元描述为：

[σ(w_0x_0+w_1x_1+w_2x_2 ... +b) ]

其中x0，x1…是输入。权重w0，w1…描述了神经元如何连接到输入。负的权重表示输入抑制神经元的激活，而正的权重则鼓励神经元的激活。权重是神经元的心脏，控制神经元的行为。说多个神经元完全相同，就是说权重相同。

卷积将为我们处理神经元的这种连线，描述所有权重以及哪些权重相同。

通常，我们一次描述一个层中的所有神经元而不是单个。方法是拥有一个权重矩阵 W：

[y=σ(Wx+b) ]

例如，我们得到：

[y_0=σ(W_{0,0}x_0+W_{0,1}x_1+W_{0,2}x_2...) ]

[y_1=σ(W_{1,0}x_0+W_{1,1}x_1+W_{1,2}x_2...) ]

矩阵的每一行都描述了将神经元连接到其输入的权重。

但是，返回到卷积层，因为同一神经元有多个副本，所以许多权重出现在多个位置。

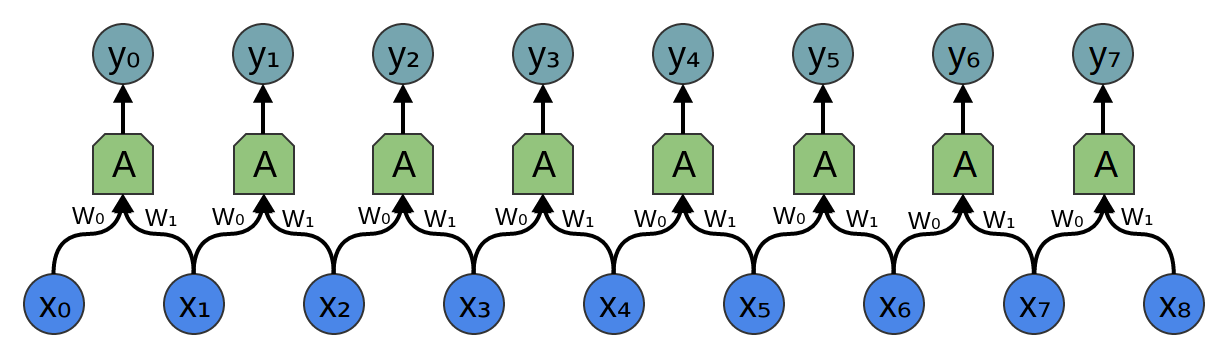
对应于等式：

[y_0=σ(W_0x_0+W_1x_1-b) ]

[y_1=σ(W_0x_1+W_1x_2-b) ]

因此，通常，权重矩阵会将每个输入连接到具有不同权重的每个神经元：

像上面的卷积层的矩阵看起来很不一样。相同的权重出现在多个位置中。而且由于神经元没有连接到许多可能的输入，因此存在很多零。

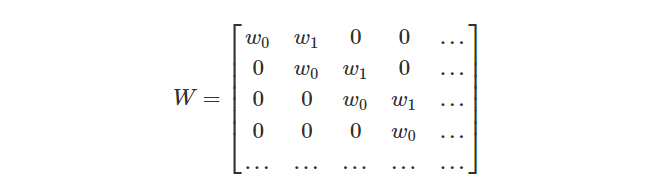
与上述矩阵相乘与[... 0，w1，w0,0 ...] 卷积相同。滑动到不同位置的功能对应于在那些位置具有神经元。

那二维卷积层呢？

二维卷积层的布线对应于二维卷积。

考虑我们上面使用卷积来检测图像边缘的示例，方法是在周围滑动一个内核并将其应用于每个面片。就像这样，卷积层会将神经元应用于图像的每个斑块。

总结

我们在此博客文章中介绍了许多数学机制，但是获得的结果可能并不明显。卷积显然是概率论和计算机图形学中的有用工具，但是从卷积的角度讲卷积神经网络有什么好处呢？

第一个优势是我们拥有一些非常强大的语言来描述网络的布线。到目前为止，我们所处理的示例还不够复杂，以至于无法清楚地看到这种好处，但是通过卷积可以使我们摆脱大量令人不快的簿记。

其次，卷积具有明显的实施优势。许多库提供高效的卷积例程。此外，虽然卷积天真地似乎是O（n2）运算，但使用一些相当深的数学见解，就有可能创建O（nlog（n））实现。我们将在以后的文章中对此进行更详细的讨论。实际上，在GPU上使用高效并行卷积实现对于计算机视觉的最新进展至关重要。

---

本文为译文，并适当添加了自己的理解，原文Understanding-Convolutions (需要翻墙才能够看到噢)