本实现主要参考了发表于2003年《软件学报》的《一个有效的多边形裁剪算法》(刘勇奎,高云,黄有群)这篇论文,所使用的理论与算法大都基于本文,对论文中部分阐述进行了详细解释,并提取了论文中一些重要的理论加以汇总。另外对于论文描述无法处理的一些情况也进行了试探性的分析。
多边形裁剪用于裁剪掉被裁剪多边形(又称为实体多边形,后文用S表示)位于窗口(又称为裁剪多边形,后文用C表示)之外的部分。裁剪的结果多边形是由实体多边形位于裁剪多边形内的边界和裁剪多边形位于实体多边形内的边界组成的。见下图

图1
后文将以这个图来描述裁剪过程,这个图形比原论文给出的图形更具代表性,最主要就在于C1这一点,论文中的图形,切割多边形没有在实体多边形中的点。所以,第一次看的人往往容易误以为切割多边形与交点组成的列表没有作用。
如图中所示,切割多边形与实体多边形分别为C1C2C3C4和S1S2S3S4S5(由于两个多边形需要同向,需要逆置切割多边形为C1C4C3C2,这个逆置也是有条件的,需要第一个交点保持不变,具体可以见代码实现),我们要得到的结果是C1-I6->I3-I4->I5(-C1)和S4->I1-I2(->S4)这两个结果多边形(其中用"-"表示切割多边形在实体多边形中的边,用"->"表示实体多边形在切割多边形中的边)
算法的实现分为三个阶段:
阶段1:计算第一个交点,并由第一个交点两多边形相互的进出性判断两个多边形是否同向,如果不同向,将切割多边形反向来使两个多边形方向一致。
阶段2:依次使用实体多边形每条边去切割裁剪多边形并将交点以正确的顺序分别插入到两个多边形的链表中。
阶段3:遍历交点列表,获得最终的结果。
后文将按照这3步来介绍相关的实现要点和代码中主要方法。最后在文章末尾还提到一些特殊情况的处理。
阶段1
阶段1要判断2个多边形是否同向(同向的重要性在后文有描述),其中很重要的一点就是求切割的交点,当然求交点在第二阶段也是很重要的,这里介绍了求交点第二阶段就不再介绍了。
(注:判断多边形是顺时针还是逆时针的方法有很多,本文的C#代码将采用原论文中的方法)
原论文中描述的方法基于一个定理:
定理1:如果两个相交多边形的边的取向相同(均为顺时针或逆时针方向),则对一个多边形是进点的交点对另一个多边形必是出点。
如果两个多边形的方向相同,对其中一个多边形求出一个进点或出点以后,另一个多边形的进出性也就确定了。这样,求出交点时只需标记其中一个多边形对另一个多边形的进出性即可。从另一个多边形角度看的进出性相反。
判断两个多边形是否同向,需要判断交点的进出性。同一个交点对于两个多边形的进出性不同,则两个多边形是同向;否则,两个多边形方向相反。
交点进出性的判定(排除切线与多边形在顶点处相交或与多边形一条边重合的情况。)
当一条直线切割多边形时,与多边形相交的第一个点是必是进点,第二个点必是出点,如此进点与出点循环出现。
当一个多边形的边切割另一个多边形时,多边形上所有交点的进出性也是交替出现。
通过上面的分析可知,整个实现过程中一个十分关键的操作就是求线段(阶段1中是求直线与多边形交点)与多边形的交点(即用线切割多边形)。并在这个过程中判断交点对于被切割多边形的进出性。
求交点
这里介绍一下原论文中给出的名为错切变化法的求交点方法。这种方法基于两直线进行错切变换后交点的x值不变来实现,通过把切线变为斜率为0的直线来使求交点的过程简化。假设切割线段为(x1,y1)、(x2,y2),被切割多边形由v1, v2 … vn构成。求交点过程可以描述如下:
1. 求斜率d,d是切线的斜率,将(x1,y1)、(x2,y2)按照这个斜率进行变化后可以得到一条水平直线,我们设这条水平直线为y=yc,则有如下方程组:

带入可得,有

说明,原论文说这里需要x1<x2(看代码实现可知x1=x2 x1>x2都是特殊处理的)。x1≠x2和y1≠y2也是需要满足的,当x1=x2时表示切线是垂直线,应在垂直方向进行切割,先求交点的坐标y。如果y1=y2则不用错切过程,直接用切线切割即可。保证x1<x2是为了保证交点插入实体多边形的顺序正确。
下图是一个例子,黑色的线是错切前的线,绿色的线是错切后的线,实线是切线,虚线是多边形上一条被切割的线:

图2
2. 将多边形上每个点vi(xi, yi)的y坐标按公式进行错切变化得到yi':

3. 对错切后多边形的每条边((xi,yi'),(xi+1,yi+1'))与切线求交点的x坐标Ixj:

如,对于前面图中的例子,带入xi, xi+1可得Ix=6.8。
接着,通过反错切就可以得到Iy,公式:

所以

经计算,Iy=4.6。最终坐标系图像:

图3
在多边形切割处理中有一个需要特别注意的问题,就是一个多边形的顶点落在另一个多边形的边上的情况。这种情况会影响交点的进出性判断,从而可能会导致错误的结果。这种点与边重合的情况可以在上述使用线切割多边形的过程中处理。我们分几种情况讨论:
1. 切线的点落在多边形的一条边上
下图可以很好的说明这种情况:

图4
当通过计算,我们发现交点坐标的x值Ix与切线的坐标x的最大或最小值相等时就发生了这种情况。
如下面的两组多边形都是这种情况:

图5
如果不考虑第二种情况,我们只需将这些坐标的x值Ix与切线的坐标x的最大或最小值相等的点不算在交点(实交点和虚交点都不统计这种情况)内即可忽略这种情况,即我们假设那个点不相交。但这种处理对第二种情况不适用,我们需要知道这个特殊的交点的进出性来决定遇到这个交点后是沿着实体多边形还是切割多边形继续前进。
对于这种情况,只需将坐标的x值Ix与切线的坐标x的最大或最小值相等的交点作为实交点即可。
2. 多边形边的一点落在切线上
如下图所示:
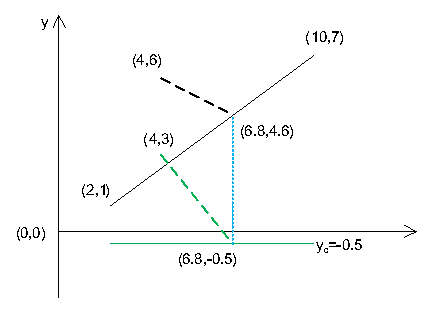
图6
当经过错切计算后,错切后的多边形的点的坐标的y值等于yc的话,表示出现了这种情况。由于被切的多边形的边不用计算交点的进出性(当然判断两个多边形方向时是个例外,也就是说判断两个多边形方向时需要选择一个一般化的交点),只需忽略这种多边形的边,不拿它们与切线计算交点即可(简单说,这种交点可以被忽略)。
如下图使用上述方法可以正确处理:

图7
3. 边重合的情况
以上两种情况的处理,由于我们没有改变多边形结点的坐标,所以不会对最终的结果产生错误的影响,是可以接受的解决方案。对于两个多边形有边重合的情况(两多边形结点重合除外,这个问题后面说),如这样两个多边形(其中实体多边形为实线,虚线的为切割多边形,后文例子同),通过上面的方法可以正确处理,且不需要特意去判断重合,我们可以将其作为情况2的一个特例:

图8
4. 当前文提到的情况1和2同时发生时,就是多边形节点重合的情况,体现在坐标系中为如下这样:

图9
看2个这种情况的典型例子:

图10
对于这种情况的处理方法,当经过错切计算后,错切后的多边形的点的坐标的y值等于yc的话,且交点的坐标的x值正好等于切线端点的x坐标,即发生当前所述情况,则我们挑多边形边上的一个点认为其有交点,而另一个点认为没有交点。还是用上图的例子来解
如果现使用I1I2依次切割多边形的边C1C2, C2C3, …我们假设如果多边形边上的第二点(对于C1C2,C2C3第二点分别为C2,C3,另外,使用第一点效果也是一样的)出现情况4时,我们认为其存在实交点。即使用I1I2切 C1C2,我们认为有一个交点,使用I1I2 切C2C3时根据上述规则它们没有交点。这样这种情况就得到正确的处理。
结果上面的介绍,对于各种交点计算都已可以处理,然后按偶奇的顺序来标记进出性也很容易了。下面来看第二阶段。
阶段2
上面介绍的方法已经可以得到交点与交点的进出性。并根据进出性判断两个多边形的方向,对于不同的向的,需要将其中一个多边形反向。下面是整个算法的另一个重点,用实体多边形的边切割裁剪多边形并将交点插入两个多边形的的链表的过程。
1. 先把切割多边形与实体多边形连成如下两个链表(前文已处理为方向一致)。

图11
2. 用实体多边形S的每条边依次切割切割多边形C,并把交点依次插入实体多边形S与切割多边形C的链表中,这个过程中同时标记该交点实体多边形对于切割多边形的进出性。
开始执行时,先使用S1S5切割切割多边形C,会产生I6, I3两个交点,可以使用S1、I6、I3和S5这几个点x坐标的位置关系来作为顺序进行插入。这样依次用S中每条边切割C并插入链表,最终得到如下模型:

图12
下面的图可以更好的看出每个链表各自的情况(注意,交点相对不同的多边形进出性是相反的,这也是多边形同向的主要特征):

图13
这样完成切割以及交点插入后就可以进入阶段3了。
阶段3
在有了上面两个链表后,遍历实体多边形和裁剪多边形链表来来获得输出多边形链表。遍历过程由实体多边形对于裁剪多边形为进点的这样一个交点开始(需要used为0)。如上图第一个这样的交点为I6。
从该进点到实体多边形链表中的下一个交点(一定为出点,对于图中这个点为I3)之间的所有实体多边形上的点全部作为结果多边形(下面的图中以红色箭头表示这样一个生成结果的过程,即沿着I6的NextS方向,对应图中实心三角箭头所指方向前进)。另外每遍历一个结点或交点就将其used置为1,下同。
由于I3是实体多边形对于裁剪多边行的出点,所以下面的过程不能继续沿着实体多边形的边继续,需要转向裁剪多边形的方向(即沿着I3的Next2方向,对应图中三角箭头方向)继续找点,直到遇到下一个交点(这个交点必然是实体多边形对于裁剪多边形的进点)。(此处论文中提到由于I3的NextC方向是裁剪多边形相对于实体多边形的进点,所以沿着NextC方向继续,正是因为两个多边形同向,由于定理1,必然可以保证I3的NextC方向是裁剪多边形相对于实体多边形的进点,所以这就是两个多边形同向的重要性。)把这些点顺序加入输出多边形。
重复这个过程(即遇到进点就沿NextS走,遇到出点就沿NextC走,另外注意,主要这个过程中遇到Vertex(不管是实体多边形的,还是裁剪多边形的),一定是沿着其Next走)直到遇到当前结果多边形起始的那个交点(对于这个例子即I6)。这样就输出了一个结果多边形。
在上面处理结束后,如果实体多边形的链表中还有used为0的交点,说明还有其它的结果多边形。找到第一个used为0的进点,然后继续上文所述的过程,得到剩余的结果多边形。直到所有used为1结束。
下图展示了连接点的过程:

图14
另一个版本:

图15
这样就可以得到结果了。
本文参考论文所实现的算法支持一般多边形,包括但不限于凹多边形等,而且经过简单修改还可以求多边形的并或差,有一定的应用范围。在输出多边形的过程中当遇到进点(实体多边形相对于切割多边形)时沿着切割多边形的方向(即交点的NextC方向),而遇到出点(实体多边形相对于切割多边形)时沿着实体多边形的方向(即交点的NextS方向),即可得到多边形的"并"。
要得到多边形的"差",只需使两个多边形开始阶段2时方向相反即可(即求交集需要多边形方向相同,求差集需要方向相反)。
对于有孔洞的多边形的切割,论文中给出了一种思路,但是具体实现太复杂,这里就没有实现。有兴趣的童鞋自己去研究下吧。基本的原理就是把有空多边形的外侧边方向和切割多边形保持一致,内侧边和外侧边方向相反,这样在内侧边与切割多边形切割时,交点的进出性可以保持正确。
由于本文使用的算法需要由交点起遍历多边形链表,所以要求切割多边形与实体多边形必须有实际交点(区别于虚焦点,即一个多边形边的延长线与另一个多边形的交点)。
下面补充讨论下两个没有实际相交的多边形。
首先看几组例子:

图16
在这种情况的处理下,仍可以处理凹多边形,将不被如下方案支持。上面几种情况,(a)切割后,结果多边形即为切割多边形。而(b)情况切割后结果即为实体多边形。对于(c),结果为空。
经过前文使用实体多边形的边切切割多边行的过程后,如果交点个数为0,则说明出现了上图的情况。对于这三种情况的区分可以使用如下方法:
取切割多边形中的一个点,如果位于实体多边形内则属于情况(a)
取实体多边形中的一个点,如果位于切割多边形内则属于情况(b)
如果以上两种情况都不成立则是情况(c)
这种判断对如下这种嵌套,但同时存在边重合的情况也适用(需要在判断时,如果点在多边形的边上也算作在多边形内部。同时这也依赖于如果两个多边形边重合就认为它们没有交点这个假设):

图17
这里涉及到一个问题是,如果一个多边形嵌套另一个多边形,如何来判断嵌套。由于当一个多边形嵌套在另一个多边形中时,这个多边形其中的任一顶点也就在另一个多边形内部。所以可以把一个多边形是否包含另一个多边形的问题转为一个多边形是否包含一个点的问题。
对于点是否在多边形中的问题,有一个经典方法可用于判断,由这个点向任意方向做一条射线(代码实现中是向右做水平射线,实现起来最简单),如果射线与多边形有奇数个交点,说明点在多边形内部,反之(包括没有交点)则说明点在多边形外部。具体可见代码实现部分。
代码实现:
采用原论文中描述的方法判断两个多变形是否同向和获取第一个交点应该同时完成,不过我实现写不出在通过一次切割即构成链表又能判断出进出性/多边形方向的代码,所以下面的实现中判断方向的切割与构成链表的切割相分离(即阶段1和阶段2把第一个交点计算了2次,第一次只是用于方向的判断)。
算法使用的数据结构
这个算法中使用2个链表来分别表示切割多边形与实体多边形。
其中结点/交点的数据结构:
public abstract class VertexBase
{
public double X { get; set; }
public double Y { get; set; }
public string Name { get; set; }
public void SetXY(double x, double y)
{
X = x;
Y = y;
}
public Point ToPoint()
{
return new Point(X,Y);
}
}
public class Vertex : VertexBase
{
[DebuggerNonUserCode]
public Vertex(double x, double y)
{
X = x;
Y = y;
}
public VertexBase Next { get; set; }
}
public class Intersection : VertexBase
{
[DebuggerNonUserCode]
public Intersection(double x, double y)
{
X = x;
Y = y;
}
public CrossInOut CrossDi { get; set; }
public bool Used { get; set; }
public VertexBase NextS { get; set; }
public VertexBase NextC { get; set; }
}
Vertex中的Next用于表示下一个节点或交点的引用(可能是Vertex也可能是Intersection),Intersection中的NextS和NextC分别存储交点在S链表中和C链表中的下一个节点或交点的引用。Intersection中的Used记录输出结果的过程中该交点是否被输出,CrossDi表示该交点处S多边形相对于C多边形的进出性。
解决方案中ArbitraryPolygonCut.cs文件包含了算法核心的代码(篇幅原因不列出代码了,后面有Github链接,自行下载查看吧),其中
List<List<VertexBase>> Cut(List<VertexBase> listS, List<VertexBase> listC)
是算法的主入口函数,里面的注释包含了几个阶段的标识,阶段一最主要的切割并判断方向的函数为:
Tuple<CrossInOut, int, bool> CutByLineForCrossDi(VertexBase v1, VertexBase v2, List<VertexBase> list, bool withIdx, int line2Idx = 0)
阶段二切割并链接节点的函数为:
List<Intersection> CutByLine(Vertex s1, Vertex s2, LinkedList<VertexBase> linkC)
上面2个切割函数还有2个Vertical结尾的函数,用于处理切线是垂直的情况。
对于完全不相交的情况,使用
List<VertexBase> ProcessNoCross(List<VertexBase> listS, List<VertexBase> listC)
函数来处理,其中调用
bool IsVertexInPolygon(VertexBase v, List<VertexBase> list)
来进行点是否在多边形内的判断。
代码附带一个测试程序,里面附带了部分保存好的测试图形(.cut结尾的文件),其包含了文档中涵盖的几种情况。也可以通过程序创建自己的图形来测试。
最后放上一个图:

代码下载:
代码可以用于任意项目中,但本实现的测试不完善,用于生产场景请再次测试。如果用于出版的文档请标明来源。
转载本文请保留链接。