题目描述
聪聪和可可是兄弟俩,他们俩经常为了一些琐事打起来,例如家中只剩下最后一根冰棍而两人都想吃、两个人都想玩儿电脑(可是他们家只有一台电脑)……遇到这种问题,一般情况下石头剪刀布就好了,可是他们已经玩儿腻了这种低智商的游戏。
他们的爸爸快被他们的争吵烦死了,所以他发明了一个新游戏:由爸爸在纸上画n个“点”,并用n-1条“边”把这n个“点”恰好连通(其实这就是一棵树)。并且每条“边”上都有一个数。接下来由聪聪和可可分别随即选一个点(当然他们选点时是看不到这棵树的),如果两个点之间所有边上数的和加起来恰好是3的倍数,则判聪聪赢,否则可可赢。
聪聪非常爱思考问题,在每次游戏后都会仔细研究这棵树,希望知道对于这张图自己的获胜概率是多少。现请你帮忙求出这个值以验证聪聪的答案是否正确。
输入格式
输入的第1行包含1个正整数n。后面n-1行,每行3个整数x、y、w,表示x号点和y号点之间有一条边,上面的数是w。
输出格式
以即约分数形式输出这个概率(即“a/b”的形式,其中a和b必须互质。如果概率为1,输出“1/1”)。
输入
5
1 2 1
1 3 2
1 4 1
2 5 3
putout
13/25
裸的点分治
记录点到分治点路径%3个数
根据常识可得
ans+=cnt[0]*cnt[0]+cnt[1]*cnt[2]+cnt[2]*cnt[1];
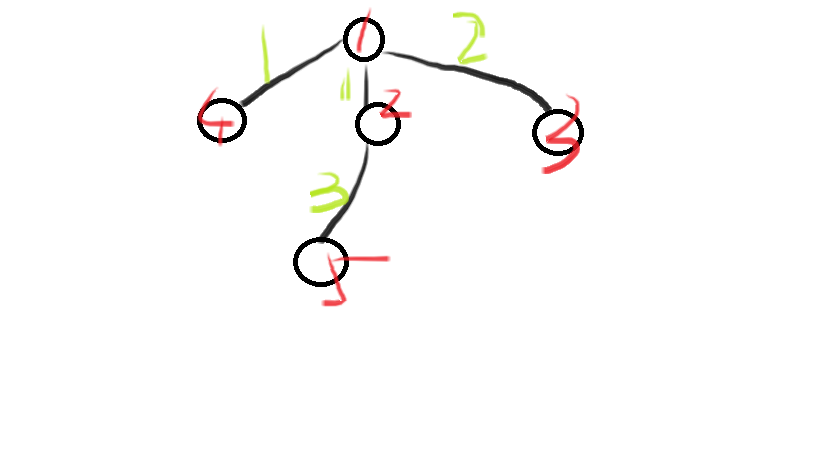
但我们可以发现,还存在以下情况
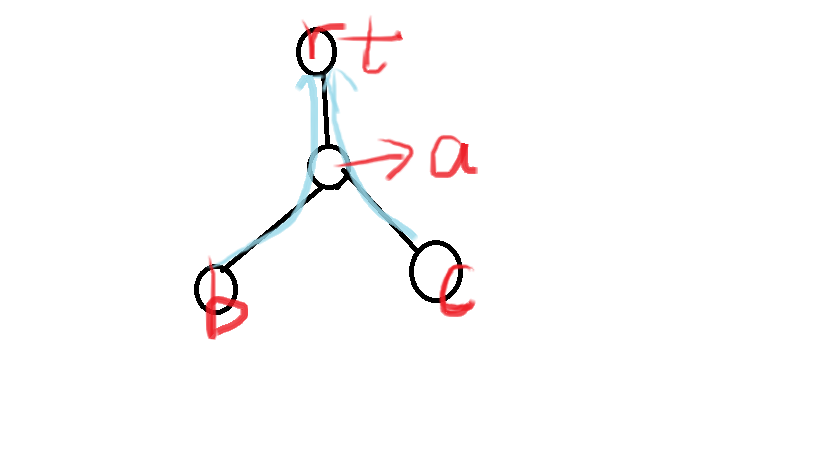
虽然b,c在同一子树里,但是我们将他们当成两条子树路径成了起来,
所以我们容斥一下,在后面访问子树时,用求解函数将错误答案统计出来,减去
这是“例题”!!!
#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)
const int maxn=20005;
using namespace std;
template<typename T>inline void rd(T&x)
{
char c;bool f=0;
while((c=getchar())<'0'||c>'9')if(c=='-')f=1;
x=c^48;
while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);
if(f)x=-x;
}
int n,m,rt,k,SIZE,hd[maxn],ANS;
int f[maxn],dis[maxn],use[maxn],cnt[10],size[maxn];
struct node
{
int to,nt,val;
}e[maxn<<1];
inline void add(int x,int y,int z)
{
e[++k].to=y;e[k].nt=hd[x];hd[x]=k;e[k].val=z;
e[++k].to=x;e[k].nt=hd[y];hd[y]=k;e[k].val=z;
}
inline void Get_rt(int x,int fa)
{
size[x]=1;f[x]=0;
for(int i=hd[x];i;i=e[i].nt)
{
int v=e[i].to;
if(use[v]||v==fa)continue;
Get_rt(v,x);
f[x]=max(f[x],size[v]);
size[x]+=size[v];
}
f[x]=max(f[x],SIZE-size[x]);
if(f[rt]>f[x])rt=x;
}
inline void Get_dis(int x,int fa)
{
++cnt[dis[x]];
for(int i=hd[x];i;i=e[i].nt)
{
int v=e[i].to;
if(use[v]||v==fa)continue;
dis[v]=(dis[x]+e[i].val)%3;
Get_dis(v,x);
}
}
inline int Get_num(int x,int D)
{
cnt[1]=cnt[2]=cnt[0]=0;
dis[x]=D%3;
Get_dis(x,0);
re cnt[0]*cnt[0]+cnt[1]*cnt[2]+cnt[2]*cnt[1];
}
inline void dfs(int x)
{
use[x]=1;ANS+=Get_num(x,0);
for(int i=hd[x];i;i=e[i].nt)
{
int v=e[i].to;
if(use[v])continue;
ANS-=Get_num(v,e[i].val);
//容斥一下,减去所有无效状态
f[rt=0]=n;SIZE=size[v];
Get_rt(v,0);
dfs(rt);
}
}
inline int gcd(int a,int b){re b?gcd(b,a%b):a;}
int main()
{
freopen("in.txt","r",stdin);
rd(n);
int x,y,z;
inc(i,2,n)
{
rd(x),rd(y),rd(z);
add(x,y,z);
}
f[rt]=SIZE=n;
Get_rt(1,0);
dfs(rt);
int d=gcd(ANS,n*n);
printf("%d/%d",ANS/d,n*n/d);
re 0;
}