CF1528B div1 Kavi on Pairing Duty

传送门

---

题意

有2n个点，相邻两点距离相等，现在要把这些点两两匹配， 一个好的匹配满足：
将每个匹配的两点连成一条线段， 任意两条线段要么长度一样， 要么一条线段包含另一条。
问共有多少种不同的好的匹配
emm..看图

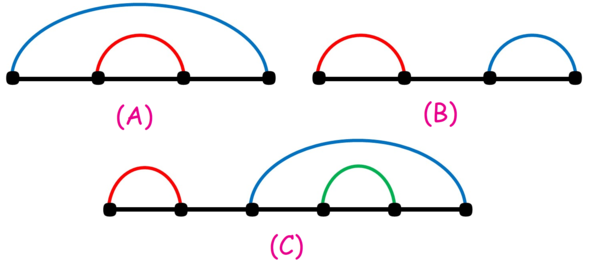
A,B是合法的，C不是， 因为红色和蓝色不符合

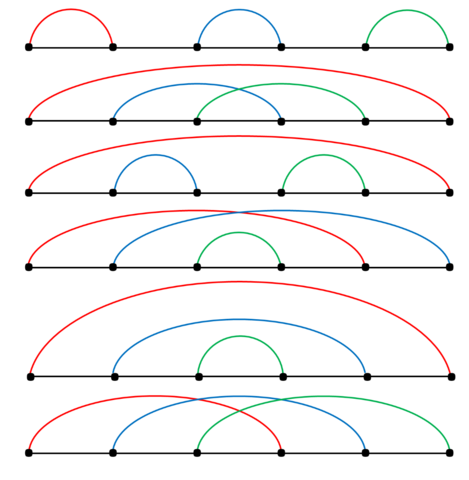
下面都是合法的情况
n=2

n=3

---

题解

我们考虑dp的思想， 每次往最外面加两个点
... -> . ... .
我们设(f_x)表示2x个点有多少种匹配
一种显然的情况是将最外面两个点匹配起来， 他们能包含里面所有的点， 所以肯定合法
此时贡献为 (f_{n-1})（最外面一对匹配起来， 里面随便怎么匹配，合法就行）
然后我们继续考虑，还有这些情况

......
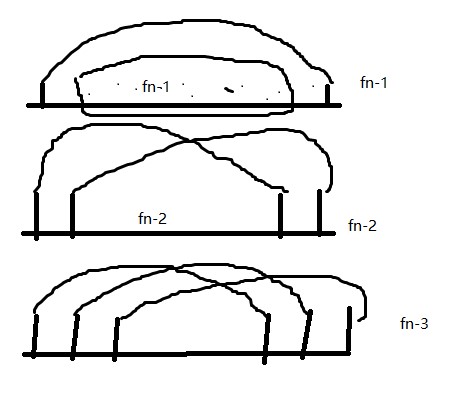
这种情况可以归结为先让最外面若干对匹配起来， 把里面完全包住， 里面随便匹配即可
手玩一下发现， 这种情况贡献为fn-1+fn-2+fn-3+......+f2+f1 (看完后面读者可以想想为什么没有f0)
除了这种情况之外， 还有另一种情况： 所有线段都相等
比如：

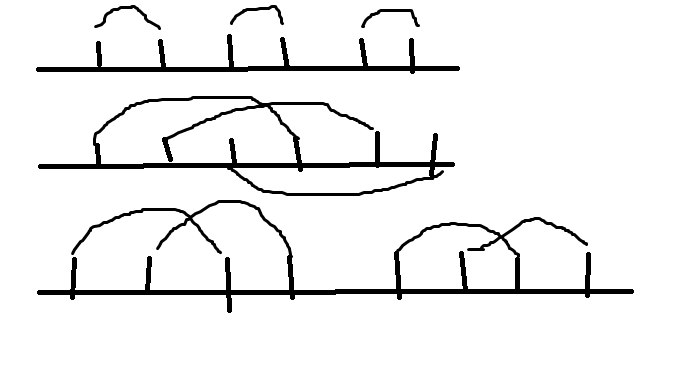
这种题反正就是手玩嘛， 你多画几张图就会发现
这种情况的贡献其实就是n的约数个数
两种情况一加就是答案了

---

然后........我居然不会求约数个数啊啊啊
但事实上对于这种，把每个数的倍数都枚举一下就可以了，调和级数啥的复杂度是O(nlogn)

---

实现

比较简单， 直接上代码

#include <iostream>
#include <cstdio>
#define ll long long
using namespace std;

int read(){
	int num=0, flag=1; char c=getchar();
	while(!isdigit(c) && c!='-') c=getchar();
	if(c=='-') flag=-1, c=getchar();
	while(isdigit(c)) num=num*10+c-'0', c=getchar();
	return num*flag;
}

const int N = 1003005;
const ll mod = 998244353;
ll f[N];

int main(){
	ll sum=1, ans=1, n=read();
	for(int i=1; i<=n; i++){
		for(int j=1; i*j<=n; j++){
			f[i*j]++;
		}
	}
	for(int i=2; i<=n; i++){
		ans = (sum + f[i])%mod;
		sum = (sum + ans)%mod;
	}
	cout << ans << endl;
}