CF1579G Minimal Coverage

给一个自认为妙好写的dp做法

显然我们可以考虑dp，容易想到最长距离可能达到1e7, 这是无法接受的。

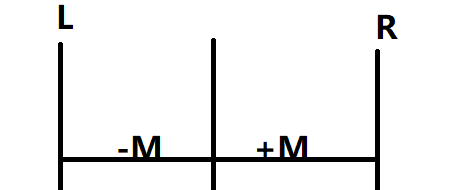
先给一个结论吧，我们假设线段的最长长度为M，那么最长覆盖不超过(2M)（向左M，向右M）。
。
可以按照如下贪心策略：如果单前结束位置离L的距离比R要远，那么下一条线段向左，反之向右。证明：如果要超过R，那么起点至少要在原点右边，此时一定向左，反之亦然。

此时容易想到的一个状态是设 (f_{i,j,k}) 前i条线段表示以j为左端点(向左覆盖的最远点)，k为结束位置的最短覆盖距离， 显然贪心来说这个距离越短越优。

此时对于 (f_i) 的每个状态，结束位置确定，考虑加入第i+1条线段，可能的结束位置和左端点只有两个， 所以转移是O(1)的。

我们发现这种方法的左右端点位置可能为负数，不好处理，而且复杂度过大，这启发我们优化状态设计。

仔细思考，我们记录左端点和结束位置，又知道覆盖长度来求出右端点，这些这的有用吗？

我们其实只是想知道结束位置与左右端点的距离即可，他们的位置具体在哪里并不重要，您把他平移一下还是一样的。所以我们考虑设 (f_{i, j})，前i线段，结束位置离左端点的距离为j时的最短覆盖，知道最短覆盖即可算出右端点距离。

转移很好写， 具体参考代码。

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
 
int read(){
	int num=0, flag=1; char c=getchar();
	while(!isdigit(c) && c!='-') c=getchar();
	if(c=='-') flag=-1, c=getchar();
	while(isdigit(c)) num=num*10+c-'0', c=getchar();
	return num; 
}
 
const int N = 1050;
const int inf = 0x3f3f3f3f;
int T, n;
int a[N*10];
int f[N*10][N*4];
 
void clear(int x){
	for(int i=0; i<N*2+10; i++) f[x][i] = inf;
}
 
int main(){
	T = read();
	while(T--){
		n = read();
		for(int i=1; i<=n; i++) a[i] = read();
		
		clear(1); f[1][a[1]] = a[1];
		for(int i=2; i<=n; i++){ 
			clear(i);
			
			for(int j=0; j<=N*2; j++){
				f[i][j+a[i]] = min(f[i][j+a[i]], j+max(f[i-1][j]-j, a[i]));
				f[i][max(j-a[i], 0)] = min(f[i][max(j-a[i], 0)], f[i-1][j]-j+max(j, a[i]));
			}
		}
		int ans = inf;
		for(int i=0; i<=N*2; i++) ans = min(f[n][i], ans);
		cout << ans << endl;
 	}
	return 0;
}