梅森数 洛谷p1045

由于梅森数是一个巨大的数我们不能一个一个2来乘，由于只存最后五百位，我们就用高精乘的思想来做；

第一问算位数证明方式如下：

2ˆp 与 2ˆp-1具有相同位数，设2ˆp的位数等于k，我们知道10ˆn的位数为n+1，自己想想看，

我们只要把底数10换成2就行了，怎么用10的n次方来表示2呢，学过对数函数的应该知道，

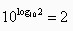所以原式子就变为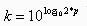，那么位数就为；

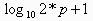#include<cmath>
#include<cstdio>
#include<iostream>
#define maxn 100000//压五位 不懂压位的可以自己看了解一下压位高精；
using namespace std;
int main()
{
    int p;
    scanf("%d",&p);
    printf("%d
",(int)((p*log10(2.0))+1))；//输出位数 int强制转换为整形；
    int s[110]={0},yu;//开个数组每个压五位不多说；
    yu=p%10;s[0]=1;//从1开始乘不多说，yu就是如同p为34这种褚步静就单独处理；
    p=p/10;//每次都从乘以2ˆ10，这一步就是算2ˆp次方有多少个2ˆ10，不难懂；
    for(int i=1;i<=p;i++)
    {
        for(int j=0;j<=100;j++)//s[j]<<10就是位运算 相当于乘以2^10;
          s[j]<<=10;//每位乘以1024这个我解释仔细一点比如一个三位数333如果乘以3，那么每一位都要乘以3，个位乘3变成9，十位也是一样；所以这里每5位都要乘以1024；
        for(int j=0;j<=100;j++)
        {
            if(s[j]>=maxn)
            {
                s[j+1]+=s[j]/maxn;//压位高精如果大于就进位
                s[j]%=maxn;
            }
        }
    }
    for(int i=1;i<=yu;i++)
   {
         for(int j=0;j<=100;j++)
                s[j]<<=1;//向左移一位就是乘以2
          for(int j=0;j<=100;j++)
        {
            if(s[j]>=maxn)
            {
                s[j+1]+=s[j]/maxn;//与上面一样的进位判断；
                s[j]%=maxn;
            }
        }
        
   }
    s[0]-=1;//梅森数最后要减1
    for(int i=99;i>=0;i--)
      {
        printf("%05d",s[i]);//输出因为压得五位所以位数不够就要补零这个知道压位方法的应该了解
        if(i%10==0)//没输出50位就提行输出格式
        printf("
");      
      }
      return 0;
}

现在比较菜之前想了很久，若有错误请大佬们指正第一次认真发题解