排序算法学习笔记（二）-- 归并排序

前言：

　　写这篇博客主要作为自己学习算法时的笔记，加深理解。可能会有很多疏漏欢迎指正。

　　代码的实现对边界的处理都是左闭右闭的区间，如果定义不同相应的代码也会有所区别。

　　参考文章：图解排序算法(四)之归并排序 

                        【图解数据结构】 一组动画彻底理解归并排序

1.归并排序

1.1 算法过程

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置
3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
4. 重复步骤3直到某一指针超出序列尾
5. 将另一序列剩下的所有元素直接复制到合并序列尾

         借这位博主（感谢大佬精心制作的图，太清晰易懂了）的图片帮助理解：

 

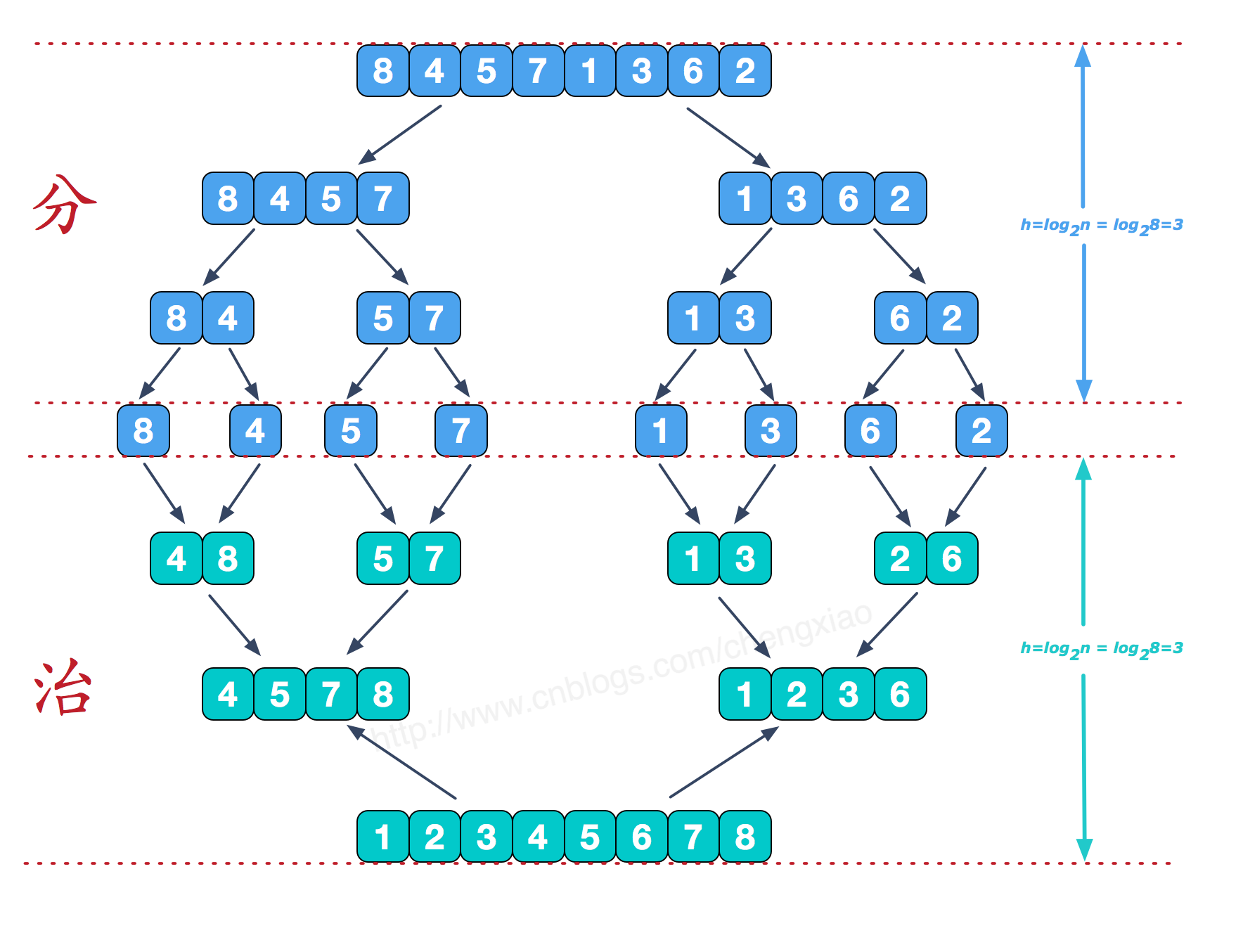
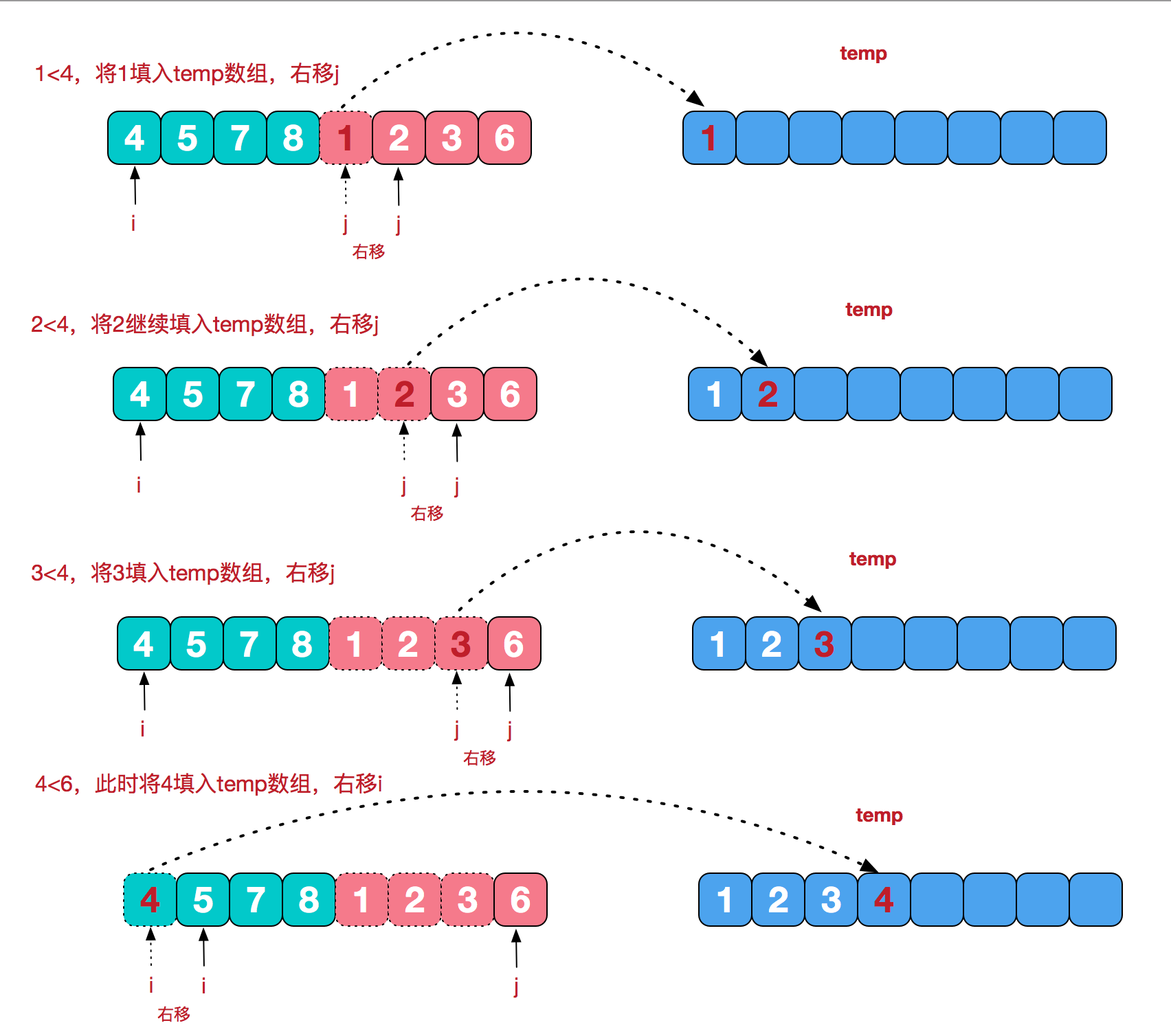
 1.2 可视化展示：

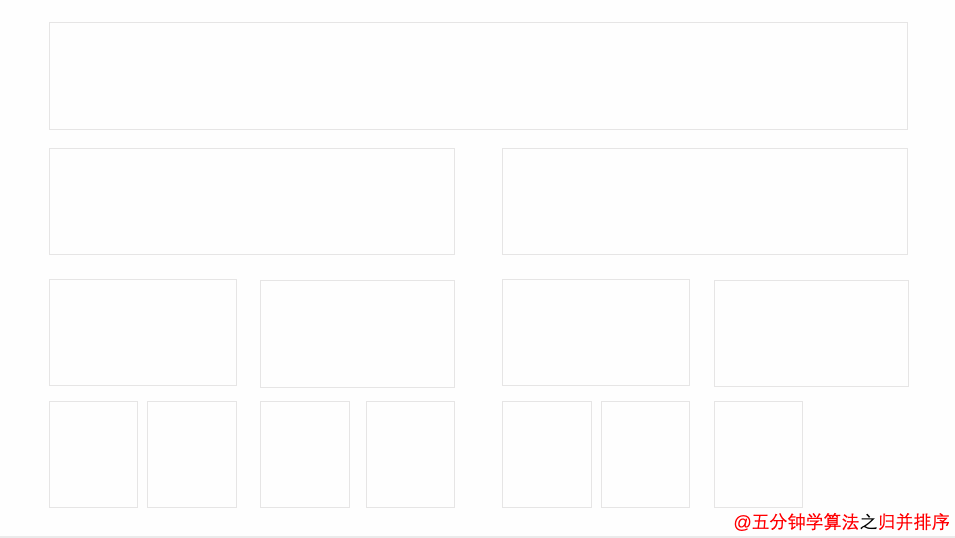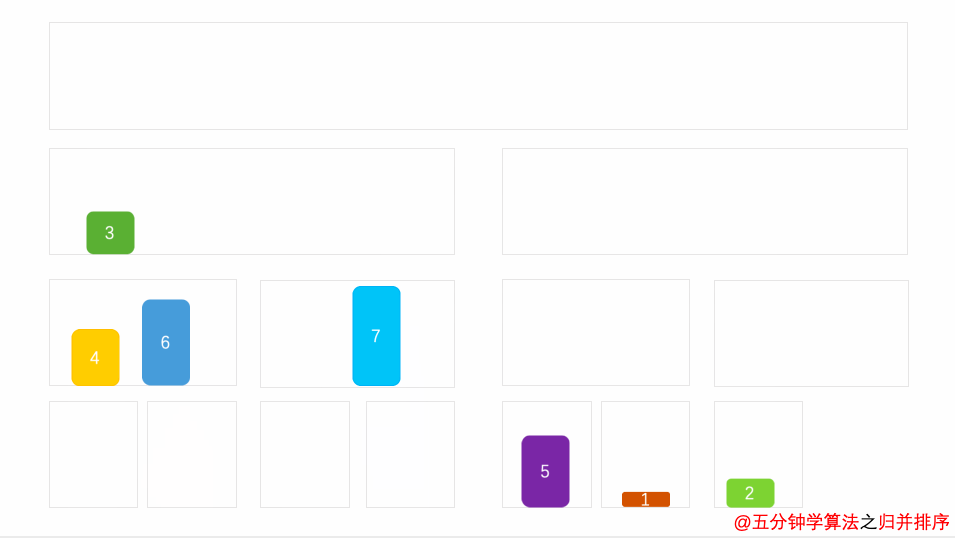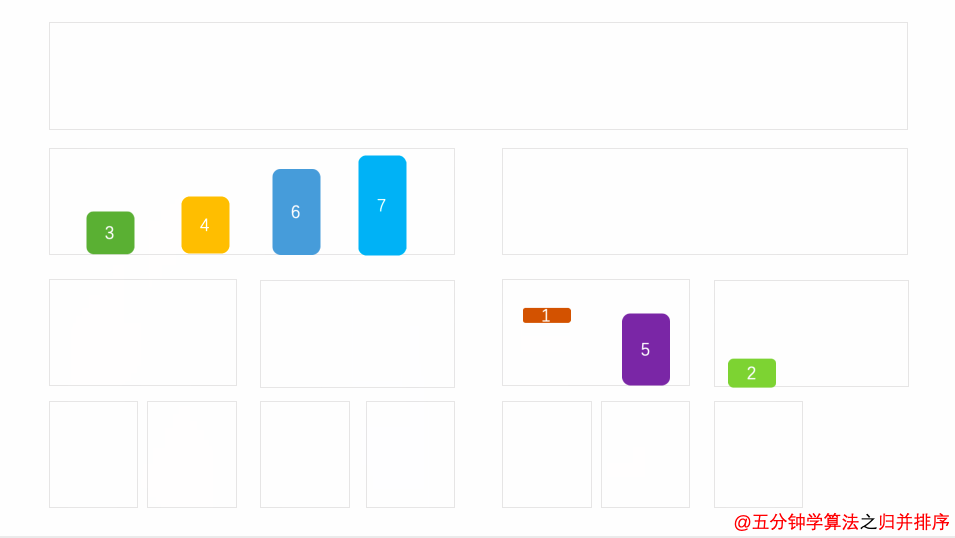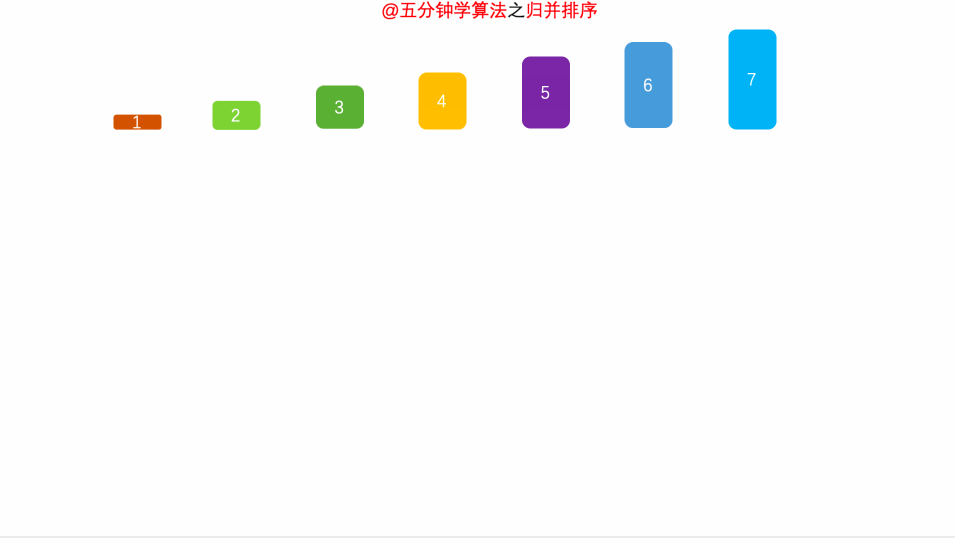
图源：https://www.cxyxiaowu.com/2176.html

1.3 代码实现

python版本：

# 将arr[l...mid]和arr[mid+1...r]两部分进行归并
def __merge(nums, left, mid, right):
    aux = []
    for i in range(left, right + 1):
        aux.append(nums[i])  # 因为这里的aux和nums对应的下标是有一个大小为left的偏移

    # // 初始化，i指向左半部分的起始索引位置l；j指向右半部分起始索引位置mid+1
    i, j = left, mid + 1
    for k in range(left, right + 1):
        if i > mid:  # 如果左半部分元素已经全部处理完毕
            nums[k] = aux[j - left]
            j += 1
        elif j > right:  # // 如果右半部分元素已经全部处理完毕
            nums[k] = aux[i - left]
            i += 1
        elif aux[i - left] < aux[j - left]:  # // 左半部分所指元素 < 右半部分所指元素
            nums[k] = aux[i - left]
            i += 1
        else:  # 左半部分所指元素 >= 右半部分所指元素
            nums[k] = aux[j - left]
            j += 1


def __merge_sort(nums, left, right):
    if left >= right:
        return

    mid = math.floor((left + right) / 2)
    __merge_sort(nums, left, mid)
    __merge_sort(nums, mid + 1, right)
    __merge(nums, left, mid, right)


def merge_sort(nums):
    __merge_sort(nums, 0, len(nums) - 1)

写代码过程中会遇到的两个小坑：

1.python中“=”只能用来修改list中已有的项，不可以用来增加新的元素那么增加新的元素，有四种方法：append(),extend(),insert(), +加号。不能像下面C++那种写法。

2.注意python中由于变量声明不需要指定类型，在递归中条件涉及除法的时候就要注意强制转型，防止陷入无穷递归。

C++版本：

// 将arr[l...mid]和arr[mid+1...r]两部分进行归并
template<typename T>
void _merge(T arr[], int l, int mid, int r) {
    T *aux = new T[r - l + 1];

        // 两个数组之间存在偏移量，需要减去这个偏移，下标才可以正确对应
    for (int i = l; i <= r; i++)
        aux[i - l] = arr[i];
       
        // 初始化，i指向左半部分的起始索引位置l；j指向右半部分起始索引位置mid+1
    int i = l;
    int j = mid + 1;
    for (int k = l; k <= r; k++) {
        if (i > mid) { // 如果左半部分元素已经全部处理完毕
            arr[k] = aux[j - l];
            j++;
        }
        else if (j > r) { // 如果右半部分元素已经全部处理完毕
            arr[k] = aux[i - l];
            i++;
        }
        else if (aux[i - l] < aux[j - l]) {  
            arr[k] = aux[i - l];
            i++;
        }
        else { // 左半部分所指元素 >= 右半部分所指元素
            arr[k] = aux[j - l];
            j++;
        }
    }
    delete[] aux;
}

template<typename T>
void __mergeSort(T arr[], int l, int r) {

    if (l >= r)
        return;

    int mid = (l + r) / 2;
    __mergeSort(arr, l, mid);
    __mergeSort(arr, mid + 1, r);
    _merge(arr, l, mid, r);
}

// 递归使用归并排序,对arr[l...r]的范围进行排序
template<typename T>
void mergeSort(T arr[], int n) {
    __mergeSort(arr, 0, n - 1);
}

 1.4 归并排序的改进

　　当面对近乎有序的数组，插入排序可以退化成近乎O（n）级别的算法，此时归并排序相比插入排序还要慢。

　　改进1 ：在merge操作前先加入一层判断， 如果左边数组最大值比右边数组最小值还要小，那么就说明已经有序，可以跳过merge的操作。

　　改进2：在递归到底的情况稍加修改， 当划分的子数组小到一定程度时，改而使用插入排序的方法，来加速算法。这里采用16作为分隔值。

python版本：

def insertion_sort(nums, left, right):
    for i in range(left+1, right+1):
        pre = i - 1
        cur_num = nums[i]
        while pre >= left and nums[pre] > cur_num:
            nums[pre + 1] = nums[pre]
            pre -= 1
        nums[pre + 1] = cur_num

def __merge_sort(nums, left, right):
    if right - left <= 15:  # 当数据规模很小的时候采用插入排序
        insertion_sort(nums, left, right)
        return

    mid = math.floor((left + right) / 2)
    __merge_sort(nums, left, mid)
    __merge_sort(nums, mid + 1, right)
    if nums[mid] > nums[mid + 1]:  # 如果已经有序就跳过merge的过程
        __merge(nums, left, mid, right)

C++版本：

template<typename T>
void __mergeSort2(T arr[], int l, int r){

    // 优化2: 对于小规模数组, 使用插入排序
    if( r - l <= 15 ){
        insertionSort(arr, l, r);
        return;
    }

    int mid = (l+r)/2;
    __mergeSort2(arr, l, mid);
    __mergeSort2(arr, mid+1, r);

    // 优化1: 对于arr[mid] <= arr[mid+1]的情况,不进行merge
    // 对于近乎有序的数组非常有效,但是对于一般情况,有一定的性能损失
    if( arr[mid] > arr[mid+1] )
        __merge(arr, l, mid, r);
}

// 对arr[l...r]范围的数组进行插入排序
template<typename T>
void insertionSort(T arr[], int l, int r){

    for( int i = l+1 ; i <= r ; i ++ ) {

        T e = arr[i];
        int j;
        for (j = i; j > l && arr[j-1] > e; j--)
            arr[j] = arr[j-1];
        arr[j] = e;
    }

    return;
}

1.5 自底向上的归并排序

　　自底向上的排序是归并排序的一种实现方式，将一个无序的N长数组切个成N个有序子序列，然后再两两合并，然后再将合并后的N/2（或者N/2 + 1）个子序列继续进行两两合并，以此类推得到一个完整的有序数组。

        来张图帮助理解：

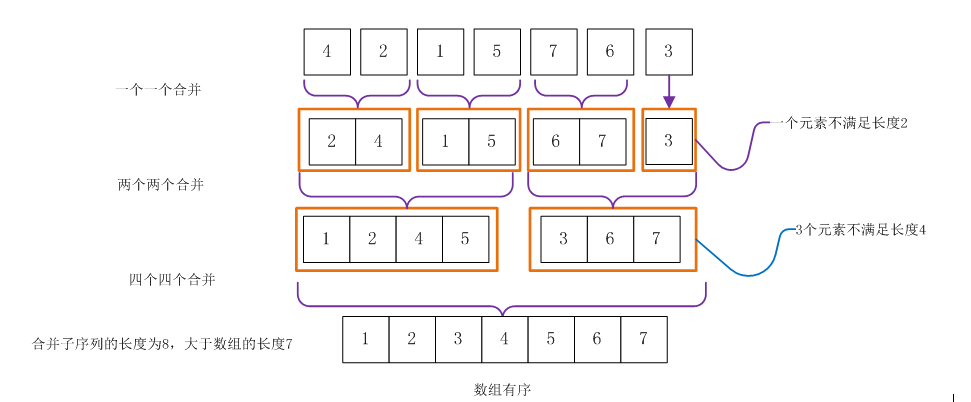
　　图源：http://images2015.cnblogs.com/blog/834468/201610/834468-20161016231626327-1390551575.png

　　代码实现：

python版本：

def merge_sort_bottom_up(nums):
    length = len(nums)
    size = 1
    while size <= length:
        for i in range(0, length - size, 2 * size):  # 这里要保证右边数组至少不为空才有意义
            __merge(nums, i, i + size - 1, min(i + 2 * size - 1, length - 1)) # 这里要保证右边数组索引不越界
        size += size

C++ 版本：

template<typename T>
void mergeSortBU(T arr[], int n) {

    for (int size = 1; size <= n; size += size) {
        for (int i = 0; i + size < n; i += 2 * size)  //右边数组要是不为空的这次归并才有意义，所以i+size<n
            __merge(arr, i, i + size - 1, min(i + 2 * size - 1, m - 1)); // 防止右边数组的右边界比数组比数组边界还大， 需要在二者之间取最小值
    }
}

// merge操作和上述是一样的，在此就不作赘述

 仔细观察可以发现，自底向上的实现方法中，对数组的访问并没有要用到索引，因此使用这种方法可以以nlog（n）的复杂度对链表实现排序！

1.6 

•   比较：自顶向下的归并排序：自顶向下划分，自底向上归并。 自顶向下的归并排序的merge操作可以理解为递归树的后序遍历。

             自底向上的归并排序：底部直接划分，自底向上归并

•  归并的空间复杂度就是那个临时的数组和递归时压入栈的数据占用的空间：n + logn；所以空间复杂度为: O(n)。 空间换时间
•  时间复杂度：O( nlogn )
•  非原地排序
•  稳定排序