郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布! 以下是对本文关键部分的摘抄翻译,详情请参见原文。

论文未全部翻译
Abstract.
本文研究了一个新的计算问题,即合数剩余阶问题(Composite Residuosity Class Problem),及其在公钥密码学中的应用。我们提出了一种新的陷阱门(trapdoor)机制,并从这一技术中推导出了三种加密方案:一种陷阱门排列方案和两种同态概率加密方案,其计算结果与RSA相当。我们的密码系统基于通常的模块化算法,在标准模型的适当假设下可以证明其安全性。
1 Background
然而,我们认为,密码研究已经悄然见证了第三类陷阱门技术的逐步出现:首先在离散对数中被识别为陷阱门,它们实际上是由高剩余度类的常见代数设置产生的。在基于二次剩余的Goldwasser-Micali的方案[9]之后,Benaloh的同态加密函数最初是为电子投票而设计的,并且依赖于素数剩余,它预示了第一次尝试:利用这一理论的纯资源。随后,Naccache和Stern[16],以及Okamoto和Uchiyama[19]分别研究了两种不同的加密方法:![]() 中平滑度的剩余和
中平滑度的剩余和![]() 中质数p的剩余,从而显著地扩展了加密率。同时,其他方案,如Vanstone-Zuccherato[28]在椭圆曲线上或Park-Won[20]探索在其他设置中使用高剩余量。
中质数p的剩余,从而显著地扩展了加密率。同时,其他方案,如Vanstone-Zuccherato[28]在椭圆曲线上或Park-Won[20]探索在其他设置中使用高剩余量。
本文提出了一种新型的陷阱门机构。与素数剩余相比,我们的技术是基于合数剩余,阶数设置为一个难以因子化的数n=pq,其中p和q是两个大素数。容易理解的是,我们相信我们的陷阱门为构想公钥密码系统提供了一个新的密码构建块。
在第2和第3节中,我们介绍了我们的数论框架,并在此背景下研究了一个新的计算问题(合数剩余阶问题),这是我们的主要假设。在此基础上,我们进一步推导出了三种同态加密方案,包括一种新的陷阱门排列。在适当的难处理性假设下,概率方案在语义上是安全的。我们所有的多项式简化都是简单的,并且是标准模型。

注:
1、欧拉函数Φ(n)的意义是求跟n互素,且小于n的元素的个数;
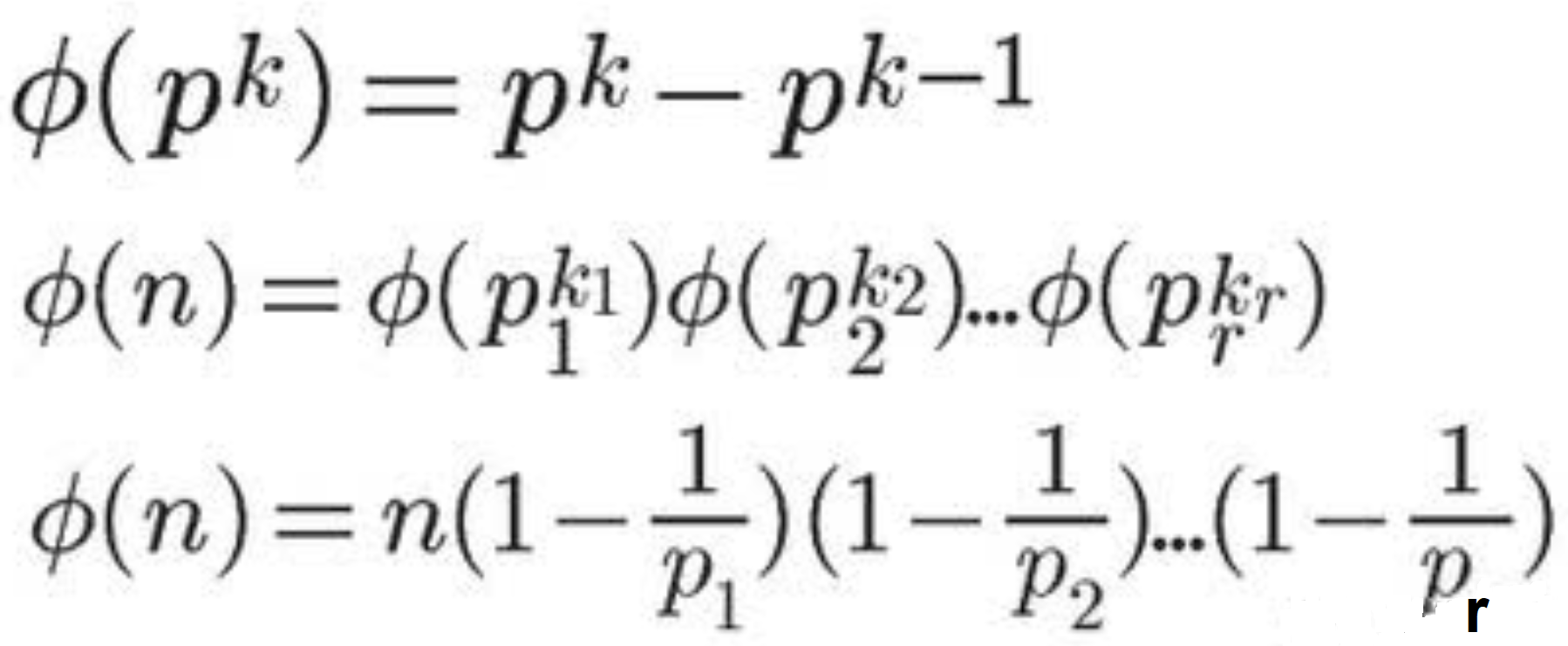
其中p1,p2,...,pr为互不相同的质数。
2、卡迈克尔函数求得是与n互素且小于n的任意一个数,在计算模n的幂次的时候,等于1的那个最小的幂次。

3、lcm(a,b)表示a,b的最小公倍数;
4、Φ(n2)=Φ(p2q2)=Φ(p2)Φ(q2)=p(p-1)q(q-1)=pq(p-1)(q-1)=nΦ(n);其中n=pq,且p,q为大质数。
2 Deciding Composite Residuosity
首先简要介绍了合数阶剩余作为高阶剩余的自然实例,并给出了一些基本的相关事实。我们设置的独创性在于使用一个平方数作为模数。如前所述,n=pq是两个大素数的积。

3 Computing Composite Residuosity Classes







4 A New Probabilistic Encryption Scheme


注:
1、gcd(m,n)求的是m与n的最大公约数;
2、Sn = { u < n2 | u = 1 mod n };
3、任意u属于Sn,L(u) = (u-1) / n;
5 A New One-Way Trapdoor Permutation
6 Reaching Almost-Quadratic Decryption Complexity

7 Efficiency and Implementation Aspects
在本节中,我们简要分析了密码系统所需计算的主要实际方面,并提供了各种提高性能的实现策略。
密钥生成
必须根据常规方法生成素数因子p和q,以使n尽可能难以分解。 快速变体(方案3)额外需要λ = lcm(p-1, q-1),其中λ是160位素数的倍数,可以通过常用的DSA-素数生成或其他类似技术来管理。 基数g可以在可被n整除的元素中随机选择,但请注意,快速变体将需要特定处理(通常将最大阶的元素提升到幂λ/α)。 通过在最后分别执行mod p2和mod q2以及中国剩余g mod p2和g mod q2的计算,可以使整个产生更容易。
加密
加密需要基数g的模幂运算。 通过明智地选择g可以显著加速计算。 作为说明性示例,假设所选择的值满足由设置施加的要求g属于B,取g = 2或小数允许一个立即加速因子1/3。 可选地,如果密钥生成过程包括特定调整,则g甚至可以固定为恒定值。 同时,用于对恒定基数进行取幂的预处理技术可以显著降低计算成本,还可以预先计算rn或gnr mod n2。
解密
通过对n-1 mod 2|n|进行预计算,可以以非常低的成本(只有一个乘法模2|n|)计算L(u),其中u属于Sn。常数参数
![]()
也可以预先计算一次。
中国剩余解密
利用中国剩余定理[6]可以有效地降低三种密码系统的解密工作量。要看到这一点,必须使用Lp和Lq函数,定义为

![]()
因此,通过分别计算信息mod p和mod q,然后重新组合模块剩余,可以更快地实现解密:
带预计算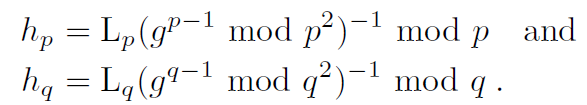
其中p-1和q-1必须用快速变量替换。
性能评估
对于每个|n| = 512,... ,2048,将位大小为|n|的模乘作为一元运算,我们假设模乘的执行时间是操作数大小的二次方,并且模数平方由相同的例行程序计算。中国剩余,以及随机数生成的概率方案,被认为是微不足道的。RSA公共指数等于F4=216+1。在我们的主方案中,参数g被设置为2,在陷阱门排列中也如此。假设其他参数、秘密指数或信息在二进制表示中包含大约相同数量的1和0。

这些估计纯粹是指示性的,并不是实际执行的结果。我们没有包括潜在的预处理阶段。密码系统中考虑到了中国剩余,即所有密码系统都不包括ElGamal。
8 Properties
在总结之前,我们想再次强调我们的密码系统的代数特性,特别是方案1和方案3。
随机自约化
这个性质实际上涉及基础的数论问题CR[n]和Class[n],并且在某种程度上,它们的弱化版本D-PDL[n,g]和PDL[n,g]。本质上,随机自约化问题和最坏情况下一样困难:RSA和离散对数问题都有这一特点。这种类型的问题被认为会产生很好的单向函数的候选者[1]。
加法同态性质

自我致盲
任何密文都可以公开更改为另一个密文,而不影响明文:

取决于所考虑的密码系统。这种属性在各种加密设置中都有潜在的应用。
9 Further Research
本文介绍了一个新的数论问题和一种基于合数剩余阶的陷阱门机构。我们基于我们的技术推导出了三种新的密码系统,在充分的不可处理性假设下,所有密码系统都是可靠的。
虽然我们没有提供任何安全性证明,以抵御选定的密文攻击,但我们相信,至少在随机预言模型中,方案1和方案3可能会有细微的修改,以使它们能够抵御此类攻击。
另一个研究主题是利用我们系统的同态特性来设计分布式加密协议(多签名、秘密共享、阈值加密等)或其他加密有用的对象。
References
。。。