郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!
arXiv:1812.06127v3 [cs.LG] 11 Jul 2019

3 Federated Optimization: Algorithms
3.1 Federated Averaging (FedAvg)
3.2 Proposed Framework: FedProx
4 FedProx: Convergence Analysis
5.2 Effect of Statistical Heterogeneity
5.3 Properties of FedProx Framework
5.4 Dissimilarity Measurement and Divergence
联邦学习涉及在大规模分布式网络中训练机器学习模型。虽然联邦平均(FedAvg)是在该设置中训练非凸模型的主要优化方法,但在实际的联邦设置中,当跨统计异质设备(即每个设备以不同的方式收集数据)学习时,它的表现并没有得到很好的理解。在这项工作中,我们引入了一个处理统计异质性的框架FedProx,它将FedAvg作为一个特例。我们通过设备差异性假设为FedProx提供了收敛保证,该假设允许我们描述网络中的异构性。最后,我们对一组联邦数据集进行了详细的实证评估,验证了我们的理论分析,并证明了相对于FedAvg,广义FedProx框架在异质网络中学习更具有稳健性和稳定性。
由电话、车辆和可穿戴传感器等远程设备组成的大型网络每天都会产生大量数据。由于用户隐私问题和系统约束(例如,通信成本、设备级计算约束和设备之间的低可用性),联邦学习已经成为一种有吸引力的范例,可以将此类网络中的模型训练推向边缘[19]。
允许局部更新和低参与度的优化方法已经成为联邦学习的实际解决方案[19,25]。这些方法在设备子集上执行可变数量的本地更新,以实现灵活和高效的通信,例如,与传统的分布式梯度下降或随机梯度下降(SGD)相比较。在当前的联邦优化方法中,FedAvg[19]已经成为非凸联邦学习的最新技术。FedAvg的工作原理很简单,就是在每个通信回合中,在总设备N的子集K « N上运行一定数量的SGD的epoch,E,然后通过中央服务器对结果模型更新进行平均。
然而,FedAvg并不是为解决联邦设置中固有的统计异质性而设计的;也就是说,数据可能在设备之间分布不一致。在实际的统计异质性背景下,FedAvg被证明在经验上存在分歧[例如,19,Sec 3],而且它也缺乏理论上的收敛性保证。事实上,最近研究收敛保证的工作仅限于不切实际的场景,例如(1)数据在设备之间共享或以IID(独立且相同分布)的方式分布,或(2)所有设备在每一轮中都参与通信[27,29,30,31,34,38]。虽然这些假设简化了分析,但也违背了实际联邦网络的关键特性。
贡献:在这项工作中,我们提出了以下两个问题:(1)我们能否在实际的、统计异质的联邦环境中对FedAvg有一个原则性的理解?(2)我们能否从理论和经验上设计出一种改进的联邦优化算法?为此,我们提出了一个异质网络的联邦优化框架FedProx,它包含FedAvg。为了将FedProx的收敛行为描述为统计异质性的函数,我们在网络中引入了一个设备差异性假设。在这个假设下,我们为FedProx在实际的异质数据联邦设置中提供了第一个收敛保证。此外,通过对大量实际联邦数据集的一组实验,我们证明了我们的理论假设反映了经验性能,并且与FedAvg相比,FedProx可以在数据跨设备异质时提高收敛的稳健性和稳定性。
大规模机器学习,特别是在数据中心环境中,在过去十年中推动了许多分布式优化方法的发展[见,例如,3,6,7,16,21,22,24,26,35,36]。然而,随着手机、传感器和可穿戴设备等计算基元的功率和普及率的增长,直接通过分布式设备网络学习统计模型,而不是将数据移动到数据中心,变得越来越有吸引力。这个问题被称为联邦学习,需要解决隐私、异质数据和设备以及大规模分布式计算网络的新挑战。
最近有人提出了针对联邦环境中特殊挑战的优化方法。与传统的分布式方法如ADMM[3]或mini-batch方法[7]相比,这些方法已经显示出显著的改进,它们允许不精确的局部更新,以便在大型网络中平衡通信与计算,并且允许在任何通信回合中激活一小部分设备[19,25]。例如,Smith等人[25]提出了一种通信效率高的原始-对偶优化方法,该方法通过多任务学习框架学习每个设备的独立但相关的模型。尽管该方法具有理论上的保证和实际的有效性,但这种方法不能推广到非凸问题,例如深度学习,在这种情况下不再保证强对偶性。在非凸的情况下,联邦平均(FedAvg)是一种基于平均局部随机梯度下降(SGD)更新的启发式方法,它在实际中表现得很好[19]。
不幸的是,FedAvg由于其本地更新方案、每轮活跃的设备很少以及数据在网络中经常以异构的形式分布的问题,使得它的分析具有相当大的挑战性。特别是,当每个设备生成自己的本地数据时,统计异质性通常是指数据在设备之间的分布不一致。最近的工作已经朝着在更简单的非联邦设置中分析FedAvg迈出了一步。例如,在IID设置中研究了并行SGD和相关变体[18,21,24,27,29,31,35,38],它们使本地更新类似于FedAvg。然而,结果依赖于一个前提,即每个局部求解器是同一随机过程的副本(由于IID假设)。这种推理方式不适用于异质环境。尽管一些工作[10,13,30,34]最近已经研究了异质环境下的收敛保证,但是他们提出了限制性假设,即所有设备都参与每一轮通信,这在现实的联邦网络中通常是不可行的[19]。此外,与本文中提出的求解器不可知框架相比,它们依赖于每个设备上使用的特殊的求解器(SGD或GD),并且将凸性[30]或一致有界梯度[34]的附加假设添加到它们的分析中。
也有一些启发式方法旨在通过共享本地设备数据或一些服务器端代理数据来解决统计异质性问题[11,12,37]。然而,这些方法可能是不切实际的:除了在网络带宽上施加负担之外,向服务器发送本地数据[12]违背了联邦学习的密钥隐私假设,并且向所有设备发送全局共享代理数据[11,37]需要努力仔细地生成或收集这样的辅助数据。
在这项工作中,受FedAvg的启发,我们探索了一个更广泛的框架FedProx,它能够处理异质联邦数据,同时保持类似的隐私和计算优势。我们分析了在局部函数不同假设下框架的收敛性。我们的假设受到求解线性方程组的Kaczmarz方法[14]的启发,该方法的类似假设已被用于分析其他情况下的SGD变种[见,例如23,28,33]。我们提出的框架允许在异类联邦网络中提高收敛的稳健性和稳定性。
最后,我们注意到,我们所提出的工作的两个方面——FedProx中的近端项和在我们的分析中所使用的有界相异假设在优化文献中已经被研究过,尽管通常具有非常不同的动机和非联邦的设置。为了完整起见,我们在附录E中进一步讨论了这项背景工作。
3 Federated Optimization: Algorithms
在这一节中,我们将介绍最近的联邦学习方法背后的关键要素,包括FedAvg,然后概述我们提出的框架FedProx。联邦学习方法(例如,19,25)设计用于处理收集数据的多个设备和协调整个网络的全局学习目标的中央服务器。联邦优化的目标是最小化:
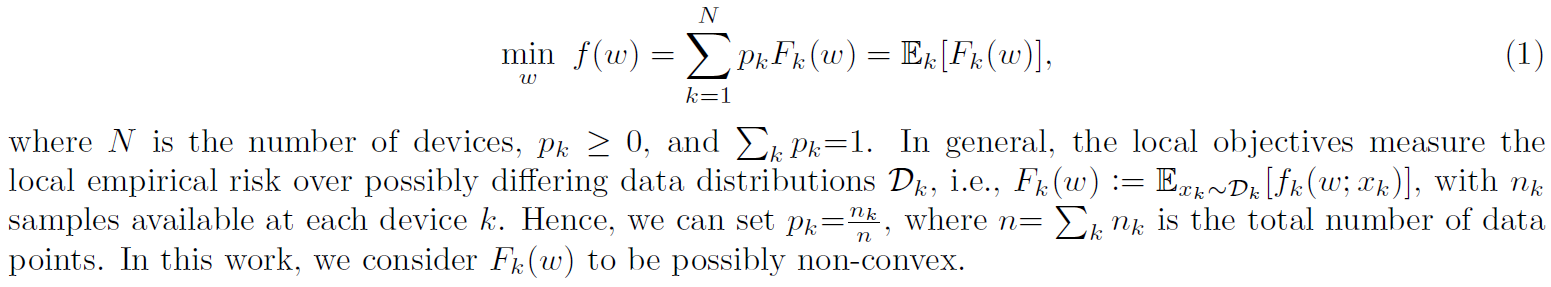
为了减少通信和处理系统约束,联邦优化方法中的一种常用技术是,在每个设备上,使用基于设备数据的局部目标函数作为全局目标函数的代理。在每次外部迭代中,选择一个设备子集,并使用局部求解器优化每个选定设备上的局部目标函数。然后,这些设备将其局部模型更新传递给中央服务器,中央服务器聚合它们并相应地更新全局模型。在这种情况下,允许灵活的性能的关键是每个局部目标可以被精确地解决。这允许根据执行的局部迭代次数调整局部计算量与通信量。我们在下面正式介绍这个概念,因为它将在整个论文中使用。
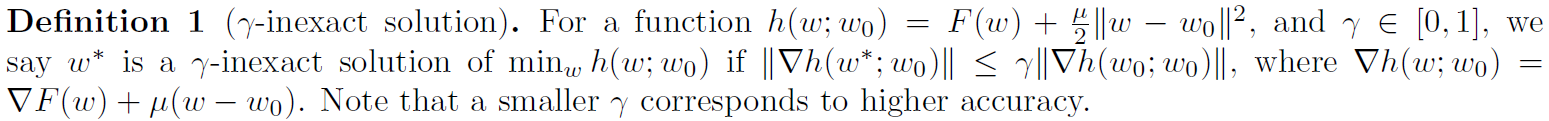
为了充分的通用性,我们在分析(第4节)中使用γ-不精确性来测量每个局部求解器的局部计算量。然而,在我们的实验(第5节)中,我们只是迭代运行局部求解器若干个局部epochs,类似FedAvg(算法1)。局部epochs的数目可以被视为γ-不精确性的一个代表,通过允许γ根据迭代和设备的不同而变化,我们能够很简单地将我们的分析加以扩展以直接覆盖这种情况,类似于[25]中的分析。
3.1 Federated Averaging (FedAvg)
在联邦平均(FedAvg)[19]中,设备k的全局目标函数的局部代理是Fk(·),而局部求解器是随机梯度下降(SGD),各设备具有相同的学习率和局部epochs数。在每一轮中,选择总设备中的子集K « N,并在局部运行E个epochs的SGD,然后对得到的模型更新进行平均。算法1总结了FedAvg的细节。

McMahan等人[19]实证表明,对FedAvg的优化超参数进行适当的调整是至关重要的。特别是,仔细调整局部epochs的数目对于FedAvg收敛是至关重要的,因为额外的局部epochs允许局部模型远离初始全局模型,从而可能导致发散。在异质设定中,局部目标可能与全局目标相差甚远,这一问题加剧恶化。通过一个更具原则性的工具来限制局部偏差量比通过启发式地限制某些迭代求解器的局部epochs的数目更有利。这一观察为下文介绍的FedProx提供了灵感。
3.2 Proposed Framework: FedProx
我们提出的框架FedProx(算法2),与FedAvg类似,它在每一轮中选择一个设备子集,执行局部更新,然后对这些更新进行平均以形成全局更新。然而,不是仅仅最小化局部函数Fk(·),设备k使用它的局部求解器来近似地最小化以下替代目标hk:
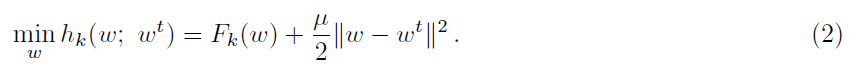
上述表达式中的近端项有效限制了局部更新的影响(通过限制它们使其接近初始模型),而不需要如FedAvg一样手动调整局部epochs数目。我们注意到,如以上所述的近端项是在整个优化文献中流行使用的工具;为了完整性,我们在附录E中对此进行了更详细的讨论。提出使用的一个重要区别是我们提出,探索,为了解决联邦网络中的统计异质性,分析这个项。我们的分析(第4节)在考虑到分布式环境中解决这样一个目标时是独特的:(1)非IID划分的数据,(2)使用任何局部求解器,(3)每个设备上的不精确更新,以及(4)在每轮中处于活跃状态的设备子集。这些假设对于在实际的联邦场景中提供这样一个框架的特性至关重要。

在我们的实验(第5.2节)中,我们看到FedProx中修改的局部子问题比原始的FedAvg对于异质数据集的收敛性更强、更稳定。在第4节中,我们还看到,近端项的使用使得FedProx更适合于理论分析(即局部目标的表现可能更好)。特别是,如果相应地选择μ,hk的海森矩阵可能是半正定的。因此,当Fk为非凸时,hk为凸;当Fk为凸时,hk为μ-强凸。请注意,FedAvg是FedProx的一个特例,其μ值为0,其中局部求解器被指定为SGD。FedProx在这方面更为通用,因为任何局部(可能是非迭代的)求解器都可以在各个设备上使用。
4 FedProx: Convergence Analysis
FedAvg和FedProx本质上是随机算法:在每一轮中,只有一小部分设备被采样来执行更新,并且在每个设备上执行的更新可能不精确。众所周知,为了使随机方法收敛到一个平稳点,需要减小步长。这与非随机方法(例如梯度下降法)不同,后者可以通过采用恒定步长来求出平稳点。为了分析常步长方法的收敛性,需要量化局部目标函数之间的差异程度。这可以通过假设数据是IID来实现,即跨设备的同质性。不幸的是,在现实的联邦网络中,这种假设是不切实际的。因此,我们提出了一个度量标准,专门测量局部函数之间的差异性(第4.1节),并在此假设下分析FedProx(第4.2节)。
在这里,我们引入一个度量联邦网络中设备之间差异性的方法,这足以证明收敛性。这也可以通过更简单的梯度有界方差假设(推论8)来满足,我们在第5节的实验中对此进行了探索。
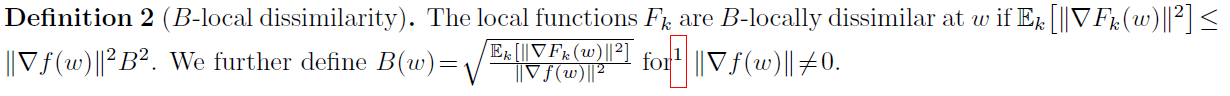

使用定义2,我们现在陈述我们在收敛性分析中使用的差异性假设。这仅要求定义2中定义的差异是有界的。

对于大多数实际的机器学习问题,不需要求解任意精确的稳定解,即ε通常不是很小。事实上,众所周知,解决超过某个阈值的问题甚至可能由于过拟合而损害泛化性能[32]。尽管在实际的联邦学习问题中,样本不是IID的,但它们仍然是从并非完全无关的分布中采样的(如果分布完全无关,那么跨设备拟合一个全局模型w是不明智的)。因此,可以合理地假设,在整个训练过程中,局部函数之间的差异仍然是有界的。在第5.4节中,我们对几个真实数据集的差异性概念进行了经验测量。
利用有界差异性假设(假设1),我们现在分析执行一步FedProx时目标的预期减少量。



我们现在给出FedProx的实验结果。在第5.2节中,我们研究了统计异质性对FedAvg和FedProx收敛性的影响。第5.3节探讨了FedProx框架的性质(μ和局部epochs E的影响)。最后,在第5.4节中,我们展示了经验收敛与有界差异性假设(假设1,推论8)之间的关系。我们在第5.1节和附录D中提供了实验设置的详细信息。所有代码、数据和实验都可以在github.com/litian96/FedProx上公开获取。
我们在不同的任务、模型和真实的联邦数据集上评估FedProx。为了刻画统计异质性并研究其对收敛性的影响,我们还对一组人工数据进行了评估,从而可以更精确地处理异质性。

真实的数据:我们还研究了五个真实数据集;统计数据汇总在附录D.1的表1中。这些数据集是从先前联邦学习的研究[4,19]中收集的。我们研究了划分MNIST[15]、Federated Extended MNIST[4,5](FEMNIST)和FMNIST*上的两个凸模型。我们研究了两个非凸模型:Sentiment140[9](Sent140)和莎士比亚全集[19](Shakespeare)。数据集、模型和工作负载的详细信息见附录D.1。
设置:对于每个实验,我们在FedAvg上调整学习率和每轮活跃设备的比率。对于每个比较,我们在所有运行中固定选择的设备和小批量顺序。我们根据全局目标f(w)记录所有指标。我们在Tensorflow[1]中实现了算法1和2;详细信息见附录D.2。注意,当局部epochs的数目E相同时,FedAvg(μ=0)和FedProx(μ≥0)在每轮执行相同的工作量——因此,我们记录的结果是以轮次的形式,而不是FLOPs(每秒浮点运算次数)或挂钟时间。
5.2 Effect of Statistical Heterogeneity
在图1中,我们使用四个人工数据集来研究统计异质性如何影响收敛(固定E为20)。从左到右,随着数据越异质,μ=0的FedProx(即FedAvg)的收敛性越差。虽然它可能会减慢IID数据的收敛速度,但我们看到设置μ>0在异质设置中特别有用。这表明,FedProx中引入的修改后的子问题在不同的统计异质性下都有利于实际的联邦设置。对于在实践中很少出现的完美的IID数据,一些启发式方法,例如如果损失继续减少,则减少μ可能有助于避免收敛减速(见附录D.4中的图7)。在接下来的章节中,我们在非人工实验中看到了类似的结果。

5.3 Properties of FedProx Framework
FedProx影响性能的关键参数是局部epochs的数目E和由µ控制缩放的近端项。直观地说,大E可能导致局部模型偏离初始点太远,从而导致潜在的发散。或者,大μ可以通过约束迭代更接近全局模型的迭代来限制迭代的轨迹,因此可能减慢收敛速度。我们使用附录D.1表1中描述的联邦数据集,在不同E和μ值下研究FedProx。
对E的依赖:我们在图2中探索E的影响。对于每个数据集,我们将E设置为1、20和50,同时保持µ=0(在这种情况下,FedProx降为FedAvg),并根据训练损失来显示收敛性。我们看到大E导致MNIST和Shakespeare的发散或不稳定。然而,在FEMNIST和Sent140上,较大的E加速了收敛。根据从图1得出的结论,我们假设这是由于FEMNIST和Sent140数据集的分布缺乏显著的异质性。我们通过观察FEMNIST*的不稳定性来验证这一假设,FEMNIST*是FEMNIST数据集的一个变体。接下来,我们将展示使用FEMNIST*代替FEMNIST的影响。
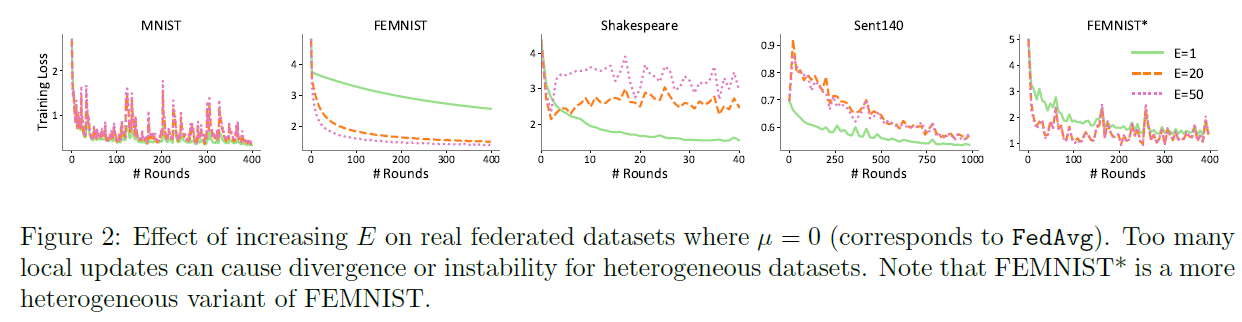
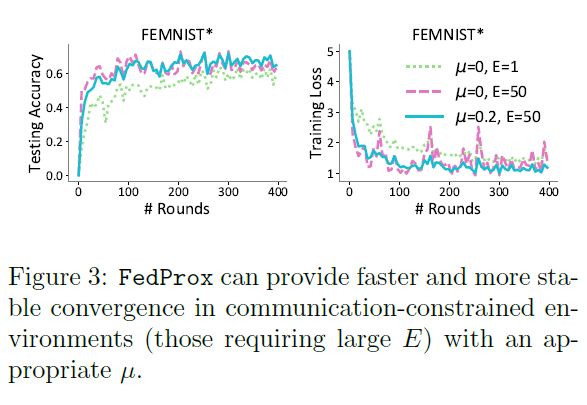
我们注意到,一个潜在的方法来处理大的局部epochs数目下FedAvg的发散或不稳定,就是保持小E。然而,这排除了精确求解局部子问题的可能性。当通信费用昂贵(这在联邦网络中很常见)时,大的局部epochs数目E在实践中也可能特别有用。事实上,在这种情况下,增加μ可以提高稳定性。在图3中,我们表明,与E=1,μ=0(慢收敛)和E=50,μ=0(不稳定收敛)相比,具有大E(E=50)和适当μ(μ=0.2)的FedProx可得更快和更稳定的收敛。
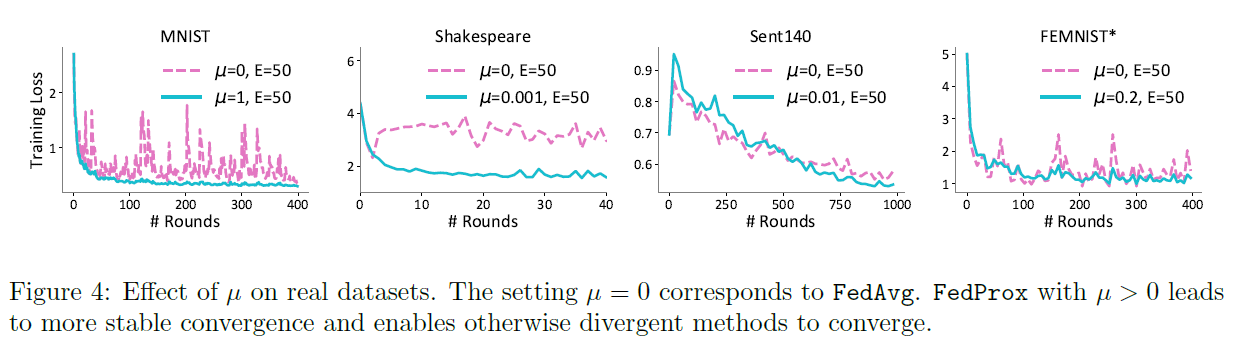
对μ的依赖:我们在图4中考虑了µ对收敛性的影响。对于每一个实验,我们都比较了µ=0和最佳μ值之间的结果。对于所有的数据集,我们观察到适当的μ可以增加不稳定方法的稳定性,并且可以迫使发散的方法收敛。在大多数情况下,它也提高了精确度(见附录D.3中的图8和图10)。在实际应用中,可以根据模型的当前性能对μ进行自适应选择。例如,一个简单的启发式方法是当看到损失增加时增加μ,当看到损失减少时减少μ。我们在附录D.4中提供了额外的实验来证明这种方法的有效性。未来的工作包括基于本文提供的理论基础,为异质数据集开发自动调整此参数的方法。
5.4 Dissimilarity Measurement and Divergence

在这项工作中,我们提出了一个分布式优化框架FedProx,以解决在联邦网络中固有的统计异质性。我们通过一个设备相异性假设形式化定义了统计异质性,这使得我们能够描述FedProx的收敛性。我们对一组联邦数据集的实际评估验证了我们的理论分析,并证明FedProx框架可以改善实际异质联邦网络中的收敛表现。