郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

arXiv:1903.11012v3 [cs.LG] 19 Aug 2019
Neural Networks, 25 November 2019
Abstract
深度强化学习(RL)在可以通过训练过的策略解决的任务上表现了出色的性能。在使用多层神经网络(NN)的前沿机器学习方法中,它起着主导作用。同时,深度RL要求对噪声的高灵敏度,不完整和误导输入数据。遵循生物学直觉,我们将使用脉冲神经网络(SNN)来解决深度RL解决方案的一些不足。先前在图像分类领域的研究表明,使用监督学习训练的标准NN(具有ReLU非线性)可以转换为性能降低可忽略不计的SNN。在本文中,我们将这些转换结果扩展到使用RL训练的Q学习NN的领域。我们提供了将标准NN转换为SNN的原理证明。此外,我们证明了SNN可以提高输入图像中遮挡的鲁棒性。最后,我们介绍了将完整的深度Q网络转换为SNN的结果,为将来的研究向鲁棒的深度RL应用程序铺平了道路。
1. Introduction
在神经网络和脑科学的巨人中,Stephen Grossberg在涉及神经处理和脑功能的生理学和数学建模的研究领域中拥有真正独特而全面的遗产。从他60多年来的大量研究成果中,我们在此强调他的研究结果,这些研究是针对神经元和层流计算的层状皮质模型进行的。同步匹配自适应共振理论(The Synchronous Matching Adaptive Resonance Theory, SMART)模型是一项突破性的研究,利用脉冲神经元中的同步振荡来描述丘脑皮质回路中的注意力学习[1]。层流计算原理后来扩展到对视觉皮层处理和视觉感知的形成进行建模[2, 3]。Grossberg的层流计算方法不仅对计算模型有重要影响,而且对硬件开发也有重要影响,它为高级芯片设计提供了蓝图,以实现各种机器学习任务,例如IBM TrueNorth[4],Intel Loihi[5]和Manchester, UK SpiNNaker[6]。这些芯片采用了脉冲神经网络,能为可持续性AI和受大脑启发的技术的未来动态发展提供所需的能源效率。
AI和机器学习(ML)的最新进展在包括ATARI游戏在内的各种测试平台上都超过了人类性能的惊人结果[7, 8, 9]。这些成功导致对AI和神经网络(包括深度强化学习(RL))的巨大兴趣。但是,严格的分析表明,深度RL容易受到输入中随机且恶意的扰动的影响,这与对抗性AI有关[10]。应用梯度下降算法的结果是受过训练的智能体学会集中精力于几个敏感区域。但是,当这些区域被遮挡或干扰时,RL智能体的性能会下降。而且,有证据表明,网络在深度RL算法中学习到的策略不能很好地泛化。当它遇到以前从未见过的状态时,即使与其他经历过的状态相似,其性能也会下降[11]。
生物系统本质上往往会非常嘈杂[12, 13],即使在影响其输入和内部状态的恶劣条件下,它们仍然可以正常运行。由于基于事件的特性,脉冲神经网络(SNN)被认为更接近生物神经元。它们通常被称为第三代神经网络[14]。脉冲是涉及神经元的内部和外部过程的量化。具有脉冲的单个神经元充当微观瓶颈,它们具有维持低间歇性噪声且不会将低于阈值的噪声传输到其邻居的能力。此外,由于网络中的脉冲神经元的群体效应和架构连接性,它们可以进一步减轻噪声的影响[15]。根据生物学直觉,我们将SNN纳入其中,以增强深度RL解决方案的优势。
SNN的重要潜在优势是其能源效率。由于基于事件的二值性质,比起传统神经网络,SNN可以支持更为有效的能源利用,尤其是在神经形态硬件上实现时[16]。在各种硬件解决方案中,忆阻器技术对神经形态计算显示出了广阔的前景[17, 18, 19]。近年来,我们目睹了神经形态硬件平台的激增,例如IBM TrueNorth和Intel Loihi [20, 4, 5]。
由于脉冲动态的不可区分性,很难使用反向传播来训练脉冲神经元[21]。SNN最近工作的一个重要方向集中在调整反向传播以适应脉冲神经元激活的基于事件的本质[22, 23, 24]。一种替代方法,旨在以生物学方式启发的本地学习规则,例如,脉冲时间依赖可塑性(STDP)来训练网络[25, 26, 27, 28, 29, 5]。
在这项工作中,我们探索了一种不同的方法,其中在SNN中根本不进行任何学习,而是将通过训练ReLU NN获得的权重转换为具有相同结构的SNN。这个想法听起来微不足道或疯狂,但仍然有足够的证据证明它确实有效。Perez-Carrasco et al.[30]首次提出了将卷积NN(CNN)转换为SNN的想法,目的是处理基于事件的传感器的输入。Cao et al.[31] 观察到ReLU神经元的激活可以映射到脉冲神经元产生的脉冲频率,并在计算机视觉基准上报告了良好的性能。
Diehl et al.[32] 提出了一种权重归一化方法,该方法可以重新缩放SNN的权重,以减少由于过度脉冲或神经元稀疏脉冲而导致的误差。他们还展示了用于MNIST分类任务的ReLU NN到SNN的几乎无损的转换。Rueckauer及其同事确定了深度卷积网络中使用的各种常见操作的脉冲等价体,例如最大池化,softmax,批归一化和Inception模块[33, 34]。这使他们能够将流行的CNN架构(例如VGG-16,Inception-V3[36],BinaryNet[37])转换为SNN[35]。他们在这些网络中实现了几乎无损的转换。所有这些目的都是针对分类任务的,尽管据我们所知,还没有关于将深度Q网络转换为SNN的先前工作。
RL和脉冲神经元的组合是自然的选择,因为动物使用半监督和强化学习来学习执行某些任务。而且,有证据表明,生物神经元是利用来自神经递质(如多巴胺)的评估反馈来学习的[38],例如在假定的多巴胺奖励预测误差信号中[39]。但是,由于脉冲神经元与ReLU人工神经元在本质上是不同的,因此尚不清楚SNN是否可以解决RL域中的机器学习问题。这就提出了一个问题:SNN是否具有表示ReLU NN相同功能的能力?更具体地说,SNN是否可以表示能够成功玩Atari游戏的复杂策略?
我们通过证明在玩Atari Breakout游戏时可以将使用RL算法训练的ReLU NN转换为SNN而不会降低RL任务的性能来回答这些问题。此外,我们表明,与原始NN相比,转换后的SNN对输入扰动的鲁棒性更高。最后,我们证明了完整的深度Q网络(DQN)[7]可以转换为SNN并保持优于人类的性能,这为将来在SNN的鲁棒性和RL研究方面铺平了道路。本文提供的结果是使用开源的BindsNET脉冲神经网络库产生的,该库可在Github上找到,网址为https://github.com/Hananel-Hazan/bindsnet。
2. Background
2.1. Arcade learning environment
Arcade学习环境(ALE)[40]是一个平台,使研究人员可以在50多种Atari 2600游戏中测试其算法。智能体通过游戏的图像帧查看环境,并通过18种可能的动作与环境进行交互,并以游戏得分变化的形式接收反馈。这些游戏是为人类设计的,因此没有实验者的偏见。游戏涉及多种不同类型,需要智能体/算法对各种任务,难度级别和时间尺度进行概括。因此,ALE已成为强化学习的流行测试平台[7]。
Breakout:我们在Breakout游戏中展示我们的结果;图1显示了游戏的框架。Breakout类似于流行的游戏Pong。播放器控制屏幕底部的球拍;请参阅图1底部的红色条。屏幕上部有成排的彩色砖块。球在砖块和玩家控制的球拍之间反弹。有4种可能的动作:向左移动,向右移动,不移动以及开火。如果球撞到砖头,则砖头破裂,比赛得分将增加。但是,如果球落到球拍下,玩家将丧命。游戏从五个生命开始,而玩家/智能体应该在耗尽生命之前将所有砖块打破。

2.2. Deep Q-Networks
强化学习算法可训练一个策略π,以最大化随着时间的推移获得的期望累积奖励。正式地,此过程被建模为马尔可夫决策过程(MDP)。给定一个状态空间S和一个动作空间A,智能体从一组可能的初始状态S0 ∈ S中的s0 ∈ S开始。在每个时间步骤t上,从t = 0开始,智能体采取动作at从st转换到st+1。通过采取动作a从状态s转换到状态s'的可能性由转换函数P(s, a, s')给出。奖励函数R(s, a)定义了在对状态s采取动作a之后,智能体收到的期望奖励。
策略π被定义为在状态π(s, a) = Pr(At = a | St = s)下动作的条件分布。给定策略qπ(s, a)的状态-动作对的Q值或动作-价值是从状态s采取动作a后遵循策略π的期望回报。
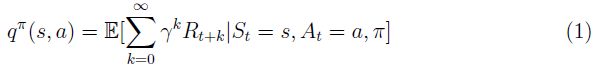
其中γ是折扣因子。动作-价值函数遵循一个Bellman方程,可以写成:

许多广泛使用的强化学习算法首先近似Q值,然后选择在每一步最大化Q值以最大化回报的策略[41]。深度Q网络(DQN)[7]是一种使用深度人工神经网络来近似Q值的算法。神经网络可以从屏幕像素和游戏分数中学习策略。已经证明,在许多Atari游戏中,DQN都超过了人类的性能。

2.3. Spiking neurons
SNN可以使用各种神经元模型中的任何一种[42, 43]。在这里,我们介绍四种不同类型的脉冲神经元。我们使用以下符号来描述神经元的动态:v(t)是随时间变化的膜电位;vrest是静息膜电位;vthresh是神经元的发放阈值;τ是神经元动态的时间常数。
- IF神经元:IF神经元是脉冲神经元模型的最简单形式。神经元简单地对输入进行积分,直到膜电位v(t)超过电压阈值vthreshold并产生脉冲。一旦产生脉冲,膜电位就重置为vreset。

- 减法IF(SubIF)神经元:SubIF神经元的行为与IF神经元类似,只是有很小的变化,当膜电位超过阈值时,神经元发放脉冲并将其膜电压重置为vreset + (v(t) - vthreshold)[44, 45, 34]。通过添加过冲电压,神经元可以“记住”上一次脉冲产生的多余电压,并且在下一个输入时将更容易发放。这减少了从ReLU NN转换为SNN中的脉冲时丢失的信息。
- LIF神经元:LIF神经元的行为与IF神经元相似。但是,对于其膜电位高于静息电位的每个时间步骤,神经元都会泄漏恒定量的电流:
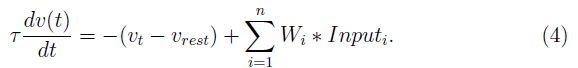
- 随机LIF神经元:随机LIF神经元基于LIF神经元。但是,如果神经元的膜电位低于阈值,则神经元可能会以与膜电位(逃逸噪声)成比例的概率发放脉冲。逃逸噪声(σ)的描述如下:
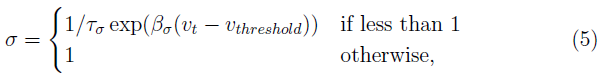
其中τσ和βσ是正的常参数。对于上面列出的脉冲模型,神经元在发放脉冲后进入不应期,在此期间它们无法发放脉冲或对输入进行积分。在本文中,为简单起见,我们忽略了来自人工神经元的转换中的不应期,并将τσ和βσ都设置为1。有关用于神经元的参数的完整列表,请参见补充材料中的表2。
请注意,与传统的人工神经网络不同,需要对SNN进行一段时间的模拟,以生成脉冲序列并解释所产生的活动。仿真是在离散的时间步骤中完成的。为了避免RL环境的时间步骤和SNN的时间步骤之间的混淆,我们用t表示RL环境的时间步骤,用nt表示SNN的时间步骤。
3. Methods
3.1. Inputs
3.1.1. Binary input
首先,根据Mnih et al.[7],我们考虑二值像素输入。每个状态都由一个80x80的二值像素图像组成。对AI Gym环境中的帧进行预处理,以创建状态用于进一步分析。裁剪AI Gym环境中的每一帧,以删除屏幕上方显示分数和剩余生命的文本。然后将图像转换为80x80的二值图像。然后从当前帧中减去前一帧,同时将所有负值都夹紧为0。然后,我们将最近的四个此类差异帧相加,以创建RL环境的状态。因此,状态是一个80x80的二值图像,其中包含最后四个状态的运动信息。
3.1.2. Grayscale input
上述二值输入不包含有关球运动方向的信息,我们认为这会使智能体混淆。为了减轻这个问题,我们根据时间对每个帧进行加权,并添加它们以创建状态。最近的帧具有最高的权重,而最远的帧具有最小的权重。在时间t,状态由最近4帧的总和组成,如下所示:
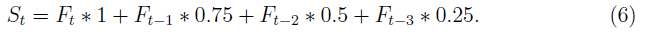
在此,St和Ft分别是时间t的状态和帧。
3.2. Network architecture
Atari游戏的DQN算法中使用的网络包括多个卷积层,然后是全连接层[7]。在这项工作中,我们从在具有一个隐含层的浅层ReLU NN上测试我们的方法开始,以证明在RL问题中使用权重传递的可行性。然后,我们继续使用与Mnih et al. [7]相同的架构的全尺寸深度Q网络。
图3显示了浅层SNN的网络架构。SNN的网络架构与ReLU NN相同,只是神经元的ReLU非线性被脉冲神经元代替。该网络由80x80输入层组成,然后是具有1000个神经元的全连接隐含层。输出层是具有4个神经元的全连接层,这些神经元给出了Breakout游戏中4个可能动作中每个动作的最优动作-价值的估计。
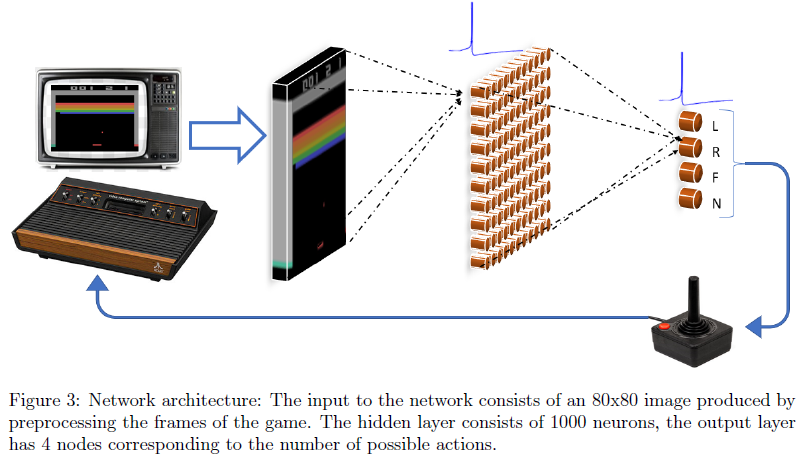
3.3. Training by reinforcement Q-learning approach
我们使用DQN算法训练网络[7]。我们使用200000的回放内存和50000的初始回放内存来训练较小的网络。我们对网络进行了超过30000个episode的训练。每个eposide都指一次有五个生命的Breakout游戏。当智能体/玩家的生命耗尽时,eposide结束。我们使用的其余超参数与Mnih et al.[7]的工作相同。有关超参数的完整列表,请参见补充材料中的表1。
3.4. Conversion of trained ReLU NN to SNN
已经使用DQN算法训练的ReLU NN被转换为SNN。对于转换后的SNN,输出层中脉冲神经元的发放率与相应动作的Q值成正比。通过用脉冲神经元替换ReLU神经元,可以将ReLU NN转换为SNN。但是,这种直接转换的结果可能会在网络中产生非常稀疏的脉冲活动。这是由于这样的事实,即脉冲神经元具有恒定的正阈值,而ReLU神经元会在大于零的任何值处激活。为了解决此稀疏性问题,针对给定输入对SNN进行了大量时间步骤(nt)的仿真,以生成足够水平的脉冲活动,从而能够可靠地估算Q值。在我们的实验中,我们仿真了nt = 500个时间步骤的SNN,并对每个输入模式重复了此模拟。为了加快过程,我们还通过增加权重来增加脉冲活动。通常,较深层的权重需要比靠近输入的层的权重更大,因为网络活动在较深层中变得稀疏。
由于脉冲神经元和ReLU神经元之间存在根本区别,因此脉冲神经元的频率无法准确表示等效ReLU神经元的输出。这是由于脉冲神经元只能输出离散的脉冲,而ReLU神经元具有连续的输出这一事实。连续活动(ReLU)转换为离散/脉冲活动是此方法的核心。脉冲神经元的输出频率受到膜电位阈值和仿真时间步骤(nt)的选择的限制。但是,我们可以通过缩放网络每层的权重来减少脉冲神经元的误差,并提高SNN的性能。我们将每层权重的缩放比例视为要优化的独立参数,以在Atari游戏测试平台上实现较高的网络性能。同一层的所有权重均按相同因子缩放,从而保留了学习的滤波器。最优权重缩放参数可以通过各种方法来搜索。Rueckauer et al.[34] 展示了一种通过归一化权重进行缩放的有用方法。他们的方法基于缩放权重,从而使大多数脉冲神经元的输出误差最小。
Rueckauer方法[34]有多种选择,可以优化从ReLU NN到脉冲NN的转换。例如,[46]在对抗性AI的背景下提供了令人印象深刻的结果。在本研究中,我们探索了几种搜索最优缩放参数的方法,包括粒子群优化(particle swarm optimization,PSO)[47]和简单的穷举网格搜索。在所研究的优化方法中,PSO产生了最优性能,在此我们简要总结一下。PSO使用粒子来评估搜索空间内各个位置的时态。粒子相互告知其先前的最优位置。每个粒子都有一个额外的速度,并且使用一组规则在每次迭代时更新粒子的速度和位置,从而可以有效地探索搜索空间。在我们的方法中,粒子位置的第n维决定值,通过该值缩放SNN的第n层。基于缩放特定位置上的坐标,可以通过评估特定网络在游戏中的性能来确定该位置的合适度。
基于PSO的网络优化证明了关于Rueckauer et al.[34]的方法,Atari游戏的性能大幅提高。该方法减少了脉冲神经元和ReLU神经元输出之间的误差。简而言之,PSO充当SNN的训练算法。PSO更适合使用DQN算法训练的网络,因为与使用交叉熵损失的图像分类任务不同,Q网络的输出值不会相差很大,因此当SNN离散化后,这难以区分。
4. Results
4.1. Performance in breakout games using shallow NNs
在ALE中测试基于SNN的智能体是一项计算量很大的任务。我们使用基于PyTorch的开源库BindsNET[29]模拟脉冲神经元。与某些替代的脉冲NN软件包相比,BindsNET的优势在于允许用户利用GPU来模拟SNN并加快测试速度。
我们使用PSO算法来确定两层中每一层的尺度;因此,搜索空间的维度D为2。群大小S使用以下公式设置:
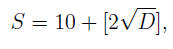
其中[u]是实数u的整数部分。在我们的实验中,群大小为S = 13。每个粒子的合适度由100次eposide的平均奖励给出。与LIF网络相比,随机LIF网络在参数空间上具有更平滑的性能。这表明,随机LIF网络在改变其权重比例时更鲁棒。可以对随机LIF神经元的逃逸噪声进行调整,以进一步提高性能,但是我们将其留待以后的工作。

表1总结了使用浅层NN的实验结果。显示的性能值是通过使用两种不同的输入编码(二值和灰度)运行100个eposide并应用两种策略(贪婪和0.05 ε-greedy)获得的。 我们测试了ReLU NN,使用LIF神经元的SNN和使用随机LIF神经元的SNN。
表1总结了针对二值和灰度输入的ReLU NN相对于SNN和随机SNN的性能。表1中具有二值输入的数据表明SNN能够表示通过RL开发的策略,并且它们的性能可能优于其来源的ReLU NN。我们可以看到,随机SNN的平均性能要好于转换后的ReLU NN。使用网格搜索找到了二值输入脉冲神经网络的最优参数。
表1显示,对于两个网络(SNN和ReLU NN),具有灰度输入的网络的性能都高于二值输入。请注意,在这些实验中,所示的奖励值明显超过了随机选择的值,即为1.27 ± 1.45。请注意,人工神经网络没有概率成分,并且通过在100个episode中用相同的初始化开始游戏,每次都能产生相同的结果(标准差为零)。我们还看到,与二值输入相比,SNN获得奖励的标准差更低,行为的随机性也更小。
图4使用奖励分布的直方图提供了有关各种分类方法性能的更多详细信息。图中的分布是使用0.05 ε贪婪策略以及二值和灰度输入确定的。
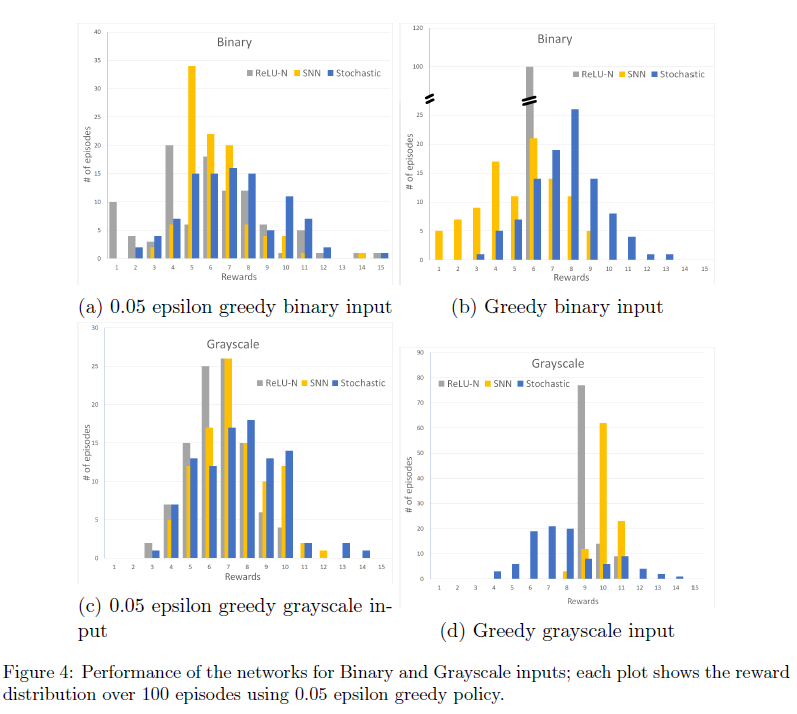
4.2. Robustness of the SNN performance
深度Q网络易受白盒和黑盒对抗攻击[10]。Witty et al.[11]表明,DQN算法学习到的策略不能很好地推广到智能体在训练期间未曾见过的状态。为了评估SNN的鲁棒性,当遮挡了跨越输入整个宽度的3像素厚的水平条时,我们使用灰度输入测试了浅Relu-N和SNN网络的性能。遮挡条的厚度对应于预处理后屏幕上球拍的厚度。通过逐步将其从屏幕底部的最低位置移到顶部,我们测试了条形图每个位置的性能。在每个episode期间,遮挡条的位置都不会改变。这是一项具有挑战性的任务,因为条可能会完全或部分遮挡球或球拍。
图5显示了ReLU NN和SNN在鲁棒性任务上的性能。x轴表示最低的遮挡像素的垂直位置。当我们在图上从左向右移动时,遮挡条从屏幕的底部移动到顶部;这代表遮挡条77个位置的总共77个实验。每个实验使用0.05 epsilon贪婪策略进行100次episode。
如图5所示,SNN在遮挡方面比ReLU NN更健壮,因为SNN(红色)的奖励通常高于ReLU NN(蓝色)的奖励。此外,ReLU NN对输入中某些位置的遮挡和扰动非常敏感。图中靠近球拍的底部显示为区域A,在砖墙所在的中间位置为区域B。当这些区域被遮挡时,ReLU-N的性能较差。这些区域的遮挡会导致ReLU NN的性能急剧下降。遮挡区域B中的某些位置,会导致ReLU NN的性能急剧下降。这可以用梯度下降更新的性质来解释。由于当球击中砖块时得分会发生变化,并且当分数变化时,网络的滤波器会学习区分这些区域,使用TD误差计算出的反向传播损失最高。因此,当这些区域被遮挡时,性能会下降。在区域A和B附近的遮挡对SNN的性能产生的负面影响要小得多。球拍可见后,我们将看到SNN的性能没有明显损失。在墙壁附近的其他敏感遮挡区域B上,ReLU NN的性能没有明显下降,SNN的性能得以保持而不会劣化。有关遮挡位置的结果的详细列表,请参阅补充材料中的表3。我们正在集中精力对此鲁棒性结果进行解释,并将其推广到一系列任务领域。

5. Performance of SNN obtained by weight transfer from Deep Q-Network
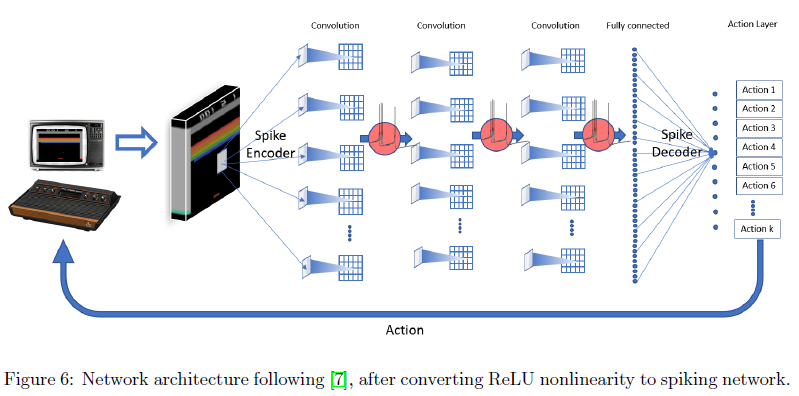
为了测试我们针对最新的大型网络的方法,我们训练了深度Q网络[7]并将权重转换为SNN。我们使用DQN的OpenAI基准实现来训练网络[48]。图6显示了从图2中的深度Q网络转换而来的SNN。由于将DQN转换为SNN需要搜索大量参数,因此我们使用已建立的参数归一化方法[34]。尽管可以使用系统参数优化方法(如PSO)明显改进此方法,但该方法显示出合理的性能。在深度Q-SNN中,我们使用了减法IF神经元。
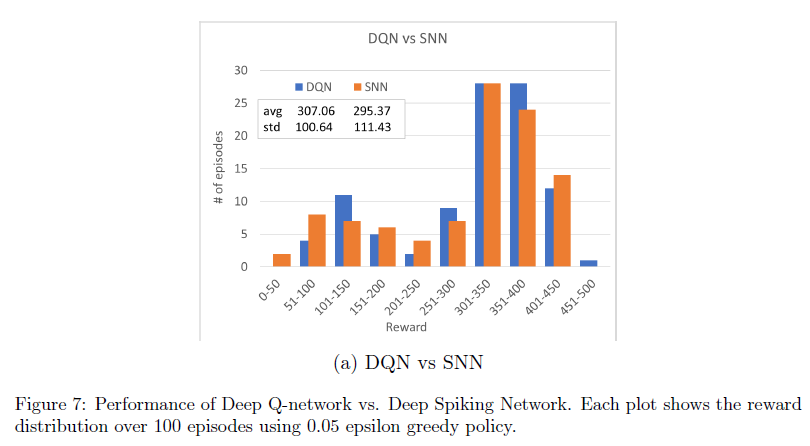
图7显示了DQN和深度SNN中奖励的分布。这些结果表明,深度Q网络可以转换为脉冲Q网络,而不会显著降低性能。在我们研究的当前阶段,我们尚未对全面训练的网络进行鲁棒性测试。我们将系统的鲁棒性研究和比较作为未来研究的目标。
6. Conclusions
在本文中,我们证明了经过Breakout游戏训练的浅层和深层ReLU NN可以转换为SNN,而不会降低性能。而且,SNN似乎对遮挡攻击显示出更高的鲁棒性。我们假设鲁棒性可能是由于脉冲神经元的二值性质,忽略了数据中的小扰动,而不像高精度传统神经网络那样。此外,从ReLU到脉冲非线性的适当优化转换方法也有助于提高结果的鲁棒性。此外,在某些情况下,SNN在以前未见过的状态下的性能优于ReLU NN。
这些结果与SNN的其他优点(例如神经形态硬件上的能源效率)相结合,表明当资源有限且输入数据带噪且可能产生误导时,SNN可能有助于补充DQN任务中强化学习的能力。