Deep learning incorporating biologically inspired neural dynamics and in-memory computing

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布

Nature Machine Intelligence, no. 6 (2020): 325-336

　　结合生物学合理的神经元的脉冲神经网络(SNN)因其独特的时间动态和能量效率而具有广阔的前景。然而，SNN与人工神经网络(ANN)分开发展，限制了深度学习进步对SNN的影响。在此，我们提出了脉冲神经元的另一种视角，它将其神经动态整合到称为脉冲神经单元(SNU)的循环ANN单元中。SNU可以作为SNN(使用阶跃函数激活)，或作为ANN(使用连续激活)。我们通过对多个任务的模拟来证明SNU动态的优势，并获得与ANN相当或更好的精度。SNU概念支持通过内存加速来有效实现训练和推理。我们使用52800个相变存储设备在基于内存的SNN加速器原型中通过实验证明了其对音乐预测任务的有效性。我们的结果为在具有挑战性的应用和神经形态硬件加速中广泛采用受生物启发的神经动力学开辟了一条途径。

　　由于神经网络在许多应用中的显著成功，近年来对神经网络的研究兴趣大大增加。神经网络的深度学习在应用于图像分类^1-3、经过端到端训练的多目标检测⁴、图像的像素级分割⁵、语言翻译⁶、语音识别⁷甚至在玩基于原始屏幕像素的电脑游戏⁸上取得记录准确性。尽管术语"神经网络"引发了与大脑复杂功能的关联，但该领域的进步是通过将1950年代的原始简单ANN范式扩展到使用反向传播训练的复杂深度神经网络获得的。人工神经网络仅从大脑结构中获取高级灵感，包括与突触互连的神经元，其神经动态代表通过非线性激活函数进行的输入-输出转换。ANN主要用于涉及静态数据的应用程序。然而，为了实现对顺序或时间数据的操作，它们的动态已经扩展到包括循环，导致所谓的循环神经网络，以及它们强大的变体，如长短期记忆(LSTM)单元¹⁰和门控递归单元(GRU)¹¹。所有这些最近的进展导致ANN在某些任务中具有类似人类的性能，尽管需要比人脑所需的大约20W的功率大得多的功率。

　　与此同时，神经科学界——其重点是了解大脑中的神经网络——一直在探索具有更多生物现实动态的架构。使用称为脉冲的稀疏异步电压脉冲来计算和传播信息，结合脉冲LIF神经元的概念^12-14，导致了SNN范式。它被用来解决有趣的认知问题^15,16，模拟抑制性神经回路的竞争动态¹⁷并利用丰富的循环时间动态¹⁸。生物启发的学习规则，例如脉冲时间依赖可塑性(STDP)^19-21，被应用于相关检测^20-26、高频信号采样²²、手写数字识别^27-29或特征学习^30-32。从实现的角度来看，SNN的固有特性导致了在神经形态计算领域探索的高效计算架构。例如，稀疏异步时间脉冲神经动态的结合导致非冯诺依曼系统的开发具有显著增加的并行性和降低的能耗，在FACETS/BrainScales³⁴、Neurogrid³⁵、IBM的TrueNorth³⁶和英特尔的Loihi³⁷等芯片中得到了证明。忆阻纳米级设备的最新突破使突触和脉冲神经元的面积和能源效率混合数字模拟实现成为可能^22-25,38，这可能导致神经计算和突触记忆的物理协同定位。此外，最近证明了ANN^41-43显著加速的乘法累加操作^39,40的内存中加速概念可以进一步改进神经形态硬件。

　　然而，尽管SNN在一些特定应用中取得了成功，但它们缺乏通用的方法来快速设计和训练适用于许多其他应用的架构。这使得不清楚如何有效地扩展它们以达到常见机器学习任务的高精度并实现低功耗神经形态硬件的优势。最近SNN的进步集中在以各种方式利用可扩展的ANN训练。首先，移植在ANN^44-47中训练的权重，可以通过SNN的平均活动与ANN¹²的相似性来实现。这种方法忽略了对时间问题的低功耗、低延迟处理至关重要的单个脉冲的时间。其次，通过开发受反向传播思想启发的SNN学习方法，用于优化单个输出脉冲的时间⁴⁸、包含膜电位的成本函数⁴⁹、包含神经活动变化的能量函数⁵⁰、利用发放率编码近似整流线性单元的SNN模型⁵¹、近似无状态二元神经元的SNN模型用伪导数训练⁵²，以及平均神经活动的梯度⁵³。一些学习方法受到了时间反向传播(BPTT)⁵⁴思想的启发，该思想考虑了时序信息。最近，已经提出了这样的方法来优化改变的SNN模型，包括通过利用不同时间形状的脉冲⁵⁵、具有自适应不可训练阈值的神经元⁵⁶或依赖于所提出的时空反向传播算法的近似LIF-like神经元，来优化包含神经元之间实值通信的SNN模型⁵⁷。可以在参考文献⁵⁸中找到对SNN的各种训练方法的详细评论。尽管在性能上有很多改进，但这些方法并没有解决训练规范SNN模型¹⁴的挑战，该模型会考虑时序信息，并且涉及额外的努力，专门针对所提出的模型推导出和重新实现深度学习见解。最后，由于缺乏可以通过设备模型或硬件在环扩展到包括硬件缺陷的系统训练方法，这限制了SNN在内存中实现的有前途的简单网络演示基于STDP的学习规则^23,28,32,59。

　　在此，我们从不同的角度看待ANN和SNN之间的关系，并探讨其对应用程序和硬件加速的影响。我们首先反思时序脉冲神经动态的本质，并提出了一种将SNN模型与其循环ANN对应物统一起来的方法，类似于参考文献^60-62中的并行发展。然后，我们提出将LIF类型脉冲神经元的生物学启发动态抽象为一个简单的循环ANN单元，称为脉冲神经单元：SNU。这种方法导致ANN构造，如果使用阶跃函数激活，则可以在离散时域中重现SNN的行为，或者在所谓的SNU软变体(sSNU)中的非脉冲ANN机制中运行。我们通过训练多达七层的基于SNU的深度网络并分析它们在三个应用程序中的性能来证明我们的方法的有效性：手写数字识别、语言建模和和弦音乐预测。为SNU获得的结果显示出比最先进的ANN获得的结果具有竞争力或更好的性能。我们注意到，在所有这些任务中，SNN模式下的SNU展示了SNN的最先进性能。考虑到sSNU，我们表明，对于所有三个任务，具有简单sSNU动态的网络都超过了循环神经网络、基于LSTM和基于GRU的网络的性能，尤其是在低精度状态下运行时。SNU的这种稳健性与其简单的结构和高效的训练相结合，可以设计出一种新型的加速器。我们提出了使用SNU概念和BPTT的具有在环训练方法的内存中硬件实现，允许对突触操作进行高效的内存中加速。此外，我们使用原型相变存储器(PCM)芯片通过实验证明了这种方法对音乐预测任务的有效性。我们观察到，这种训练方法还可以弥补硬件实现的固有缺陷和有限精度，尤其是PCM技术。这些结果表明，灵活且准确的基于SNU的深度学习为推理应用程序提供了节能的神经形态计算硬件。

Spiking neural unit

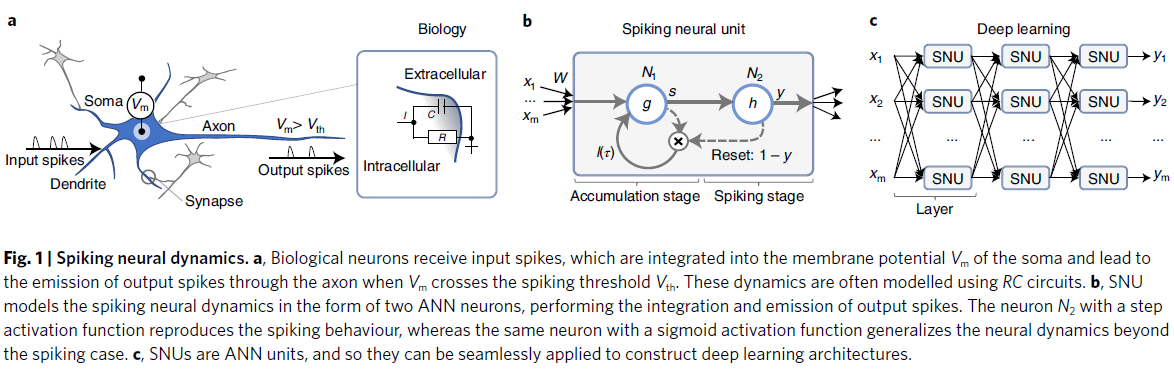
　　在简化的视图中，生物神经网络由通过突触互连的神经元组成，突触在树突处接收输入脉冲并通过轴突发出输出脉冲，如图1a所示。神经元膜将细胞内空间与细胞外空间隔开。在没有输入的情况下，膜电位保持静止值，并通过树突整合突触后电位而改变。在神经元充分激发后，由于电流通过细胞膜中的离子通道传输，会产生输出脉冲。基于Hodgkin和Huxley将神经元膜离子交换动态抽象为电阻-电容(RC)电路⁶³，SNN实现中的脉冲活动通常使用LIF神经元建模。它包含一个状态变量V_m，对应于膜电位，其动态由微分方程¹⁴描述：

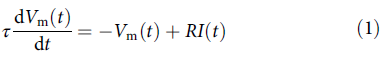
或其离散时间近似，假设离散化步长ΔT：

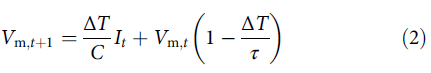
其中R和C分别代表神经元细胞体的电阻和电容，τ = RC是神经元的时间常数，I(t)是来自突触的输入电流。神经元 j 的突触接收脉冲x_i(t)并使用突触权重W_LIF,ji调节它们，以向神经元细胞体提供输入电流。如果我们不考虑突触和树突的生物现实模型的时间动态，输入电流可以定义为I_t = W_LIFx_t。输入电流被整合到膜电位V_m中。当V_m在时间 t 超过发放阈值V_th时，会发出一个输出脉冲：y(t) = 1，并且膜电位重置为静息状态V_rest，通常定义为等于0。这种方法提供了一个基本框架用于分析SNN研究中经常探索的LIF动态。

　　在此，我们将LIF动态的高级抽象引入到ANN单元中，我们将其称为脉冲神经单元：SNU。SNU包含两个ANN神经元作为子单元：N₁，它模拟膜电位积累动态，N₂，它实现脉冲发放，如图1b所示。膜电位状态变量的积分动态是通过在积累阶段与N₁的单个自循环连接来实现的。脉冲发放是通过具有阶跃激活函数的神经元N₂实现的。同时，N₂的激活通过门控N₁处的自循环连接来控制状态变量的重置。因此，SNU——LIF神经元的离散时间抽象——代表了一种结构，它可以直接作为ANN框架中的神经单元实现，它可以扩展到深层架构，如图1c所示。遵循ANN约定，在方法中详细解释，控制在SNU层中发生的计算的公式如下：

其中s_t是N₁个子单元计算的内部状态变量的向量，y_t是N₂个子单元计算的输出向量，g是输入激活函数，h是输出激活函数，⊙表示逐点向量乘法。

　　N₁的激活函数g可以对膜电位值进行额外的假设，例如，如果设置为标准的整流线性激活函数，膜电位值将受到静息状态V_rest = 0的限制。方法中描述了替代输入激活函数。输入由突触权重矩阵W加权，没有偏置项。自循环权重l(τ) = 1 – ΔT/τ，应用于之前的状态价值s_t−1，对离散时间段(t −1; t)对应于物理时间段ΔT。如果l(τ)固定为1，则状态不会衰减并且SNU对应于没有泄漏项的IF动态。最后一项(1 − y_t−1)依赖于脉冲输出的二值来保持状态或在脉冲发放后重置状态。

　　N₂的激活函数h决定了整个单元的输出。我们探索了两个激活函数。首先，阶跃激活函数h(a)返回1(如果a > 0，则对应于输出脉冲)，否则为0。在这种情况下，SNU的参数对应于等式(1)中引入的LIF神经元的参数，ANN框架中SNU的动态对应于SNN框架中的LIF，如拓展数据图1中所述。此外，如补充说明1中所述，SNN的各种其他生物学合理的神经功能，例如侧向抑制和自适应脉冲阈值，可以合并到SNU中。其次，我们考虑一个sigmoid激活函数，SNU保留了时间积分动态，并具有模拟比例重置的额外有趣特性，即输出的大小决定了保留膜电位状态变量的比例。这种方法导致了SNU单元的软版本，它结合了ANN中SNN的生物启发神经动态。这些动态与标准SNN和常见的循环ANN的动态不同。

　　LSTM和SNU的并排图示如图2a, b所示。两个单元在单元边界内都有一个循环，以灰色绘制。同时，这种描述能够识别SNU的独特特征，即内部状态循环内的非线性变换g、粗体绘制的参数化状态循环连接、粗体绘制的状态输出连接对输出激活函数h的偏差，以及由输出y控制的直接复位门(1 − y)。补充说明2包含与各种循环ANN单元的深入比较。此外，补充说明2中的分析表明，当SNU用于深度学习架构时，它们对与梯度数值稳定性相关的问题的弹性与LSTM相似。

　　在网络级别，SNU可以选择性地通过循环连接互连，这可能对某些SNN架构有益^18,56。然而，SNN社区的标准方法是依赖于前馈架构的内部状态^{17,20,21,23,25–30,32}。使用前馈状态架构解决时间问题具有一系列深远的优势。从实现的角度来看，不需要在同一层内的神经元输出和神经元输入之间的全连接。这使得高度并行的软件实现或神经形态硬件设计成为可能。从理论的角度来看，SNU的前馈网络是最简单的时间架构，它创建了一类用于时间处理的ANN架构，如图2c所示。对于具有m个输入的n个神经元层，SNU的参数数量为(m + 1)n，这相当于最简单的前馈ANN中的参数数量，如图2d所示。与常见的时序ANN(即循环神经网络和基于GRU或LSTM的网络)相比，基于SNU的网络具有最少的参数数量。

　　除了降低计算复杂度之外，少量的参数和简单的结构能够实现高效的硬件实现。我们评估了SNU概念对神经形态平台操作的影响。具体来说，通过SNU表达的ANN和SNN的组合可以用于支持两种网络的统一硬件设计方法。此外，这种方法有助于将SNN轻松集成到新兴的内存加速架构中。例如，补充说明3描述了这种基于内存的统一ANN-SNN架构概念。

Simulations

　　我们首先评估了基于SNU的网络的生物启发动态的性能，与以全精度运行的ANN相比。然后，为了评估神经形态实现的硬件要求，选定的模型用32位到2位的精度值进行模拟。以全精度模拟的任务包括：使用MNIST数据集进行手写数字识别⁶⁴、使用Penn Treebank数据集进行语言建模⁶⁵以及使用Johann Sebastian Bach合唱数据集进行和弦音乐预测⁶⁶。第一项任务的输入涉及静态数据，使用常见的SNN发放率编码约定进行编码，该约定使每个像素的灰度信息能够通过输入脉冲的发放率进行传达。剩下的两个数据集包含二值输入序列，因此它们直接输入到脉冲网络中。我们的目标是比较基于SNU的网络与最先进的SNN以及使用类似训练设置的常见ANN的准确性。所有网络均使用BPTT算法进行训练。为此，SNU结构随时间展开，即计算图及其参数为每个时间步长复制，如扩展数据图2所示。对于SNN模式下的SNU，其中h是不可微的阶跃函数，我们遵循在反向传播中使用伪导数的方法，类似于使用BPTT训练脉冲神经元的其他并行工作^56,62。具体来说，我们使用tanh的导数作为伪导数。训练的其他技术细节、输入编码和网络架构在方法中进行了描述。

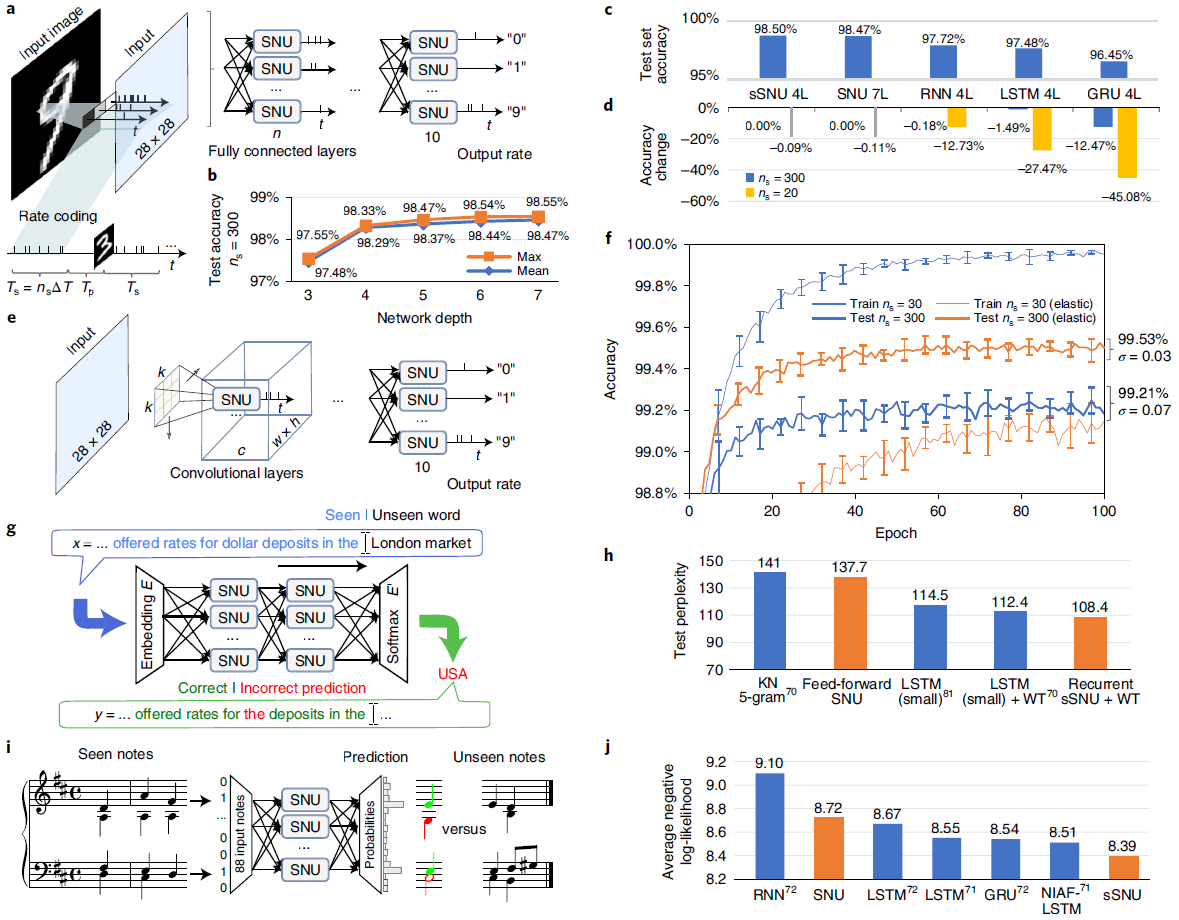
　　对于手写数字识别，我们首先评估了深度对基于全连接SNU的SNN的影响，如图3a所示。根据深度学习的见解，我们不断增加网络深度，这已被证明对于实现更高的准确性至关重要。如图3b所示，7层SNN的平均识别准确率达到98.47%。与方法中描述的各种循环神经网络、基于LSTM和基于GRU的类似架构的网络相比，基于SNU的网络实现了最高的准确度，如图3c所示。在4层网络中使用sSNU获得了98.5%的最佳结果。此外，我们评估了经过训练的网络对更具挑战性的SNN评估惯例的泛化^28,29。在此，具有连续数字的输入形成一个连续流，即暂停期设置为T_p = 0(参见图3a底部的解释)，当输入的数字改变时，网络必须在不接收明确信息的情况下对它们进行分类。无论测试序列的时间步数n_s是多少，我们都观察到在基于SNU的网络中几乎没有精度损失，相比之下，接收短序列的最先进ANN的损失高达45%以上，如图3d所示。

　　其次，为了进一步提高识别精度并同时说明SNU概念如何直接受益于深度学习的进步，我们实现了一个基于卷积SNU的SNN，如图3e所示，在扩展数据图3a中有更详细的说明。我们使用了与ANN模型中相同的架构、训练设置和超参数⁶⁸，但将其应用于发放率编码的MNIST数据集。在100个epoch之后，如图3f所示，在扩展数据图3b, c中更详细地说明，我们获得了原始数据集训练平均准确率99.21%和使用弹性失真预处理的图像训练的平均准确率99.53%⁶⁹。这些充当正则化器——降低训练准确度，但提高测试准确度。获得的准确度超过了各种最先进的SNN实现，如扩展数据图3d所示。

　　语言建模任务涉及根据先前观察到的单词序列的上下文预测下一个单词，如图3g所示。尽管输入数据缺乏明确的时间概念，但我们假设每个连续的单词都是在后续时间步长中输入的。这并没有模拟阅读中涉及的大脑特定的复杂性和时间尺度，而是遵循ANN方法。同样，我们重用了深度学习的见解，并构建了一个具有输入嵌入和softmax输出层的通用架构⁷⁰。

　　训练进度绘制在扩展数据图4a中。该架构的基于前馈SNU的版本实现了137.7的测试困惑度，这优于传统的NLP方法，例如"5-gram"，如图3h所示。据我们所知，这是在Penn Treebank数据集上使用SNN执行语言建模的第一个示例，我们的结果设置了SNN最先进的性能。具有循环连接的sSNU的应用将结果提高到108.4，超过了没有随机失活的最先进的ANN，如扩展数据图4b所示。

　　和弦音乐预测的任务是在每个时间步骤预测要在连续时间步骤中播放的音符集，如图3i所示。与之前的任务类似，我们使用了带有脉冲输入和脉冲隐含神经元的混合架构，但具有sigmoidal神经元的输出层，允许将相同的公式应用于最先进的ANN的损失，并允许获得的损失值的直接比较^71,72。基于SNU的网络实现了8.72的平均损失，并为Johann Sebastian Bach chorales数据集设置了SNN最先进的性能。一个基于sSNU的网络进一步将平均损失降低到8.39，如图4c中详细绘制的扩展数据，并超过了最先进的 ANN，如图3j所示。与LSTM的无输入激活函数(NIAF)变体的下一个结果相比，使用少于25%的参数获得了结果，如扩展数据图4d所示。

　　补充说明4中包含了通过侧向抑制的生物学启发功能增强的SNU、接收实值非脉冲输入和训练脉冲时间生成对抗网络的sSNU的其他结果。

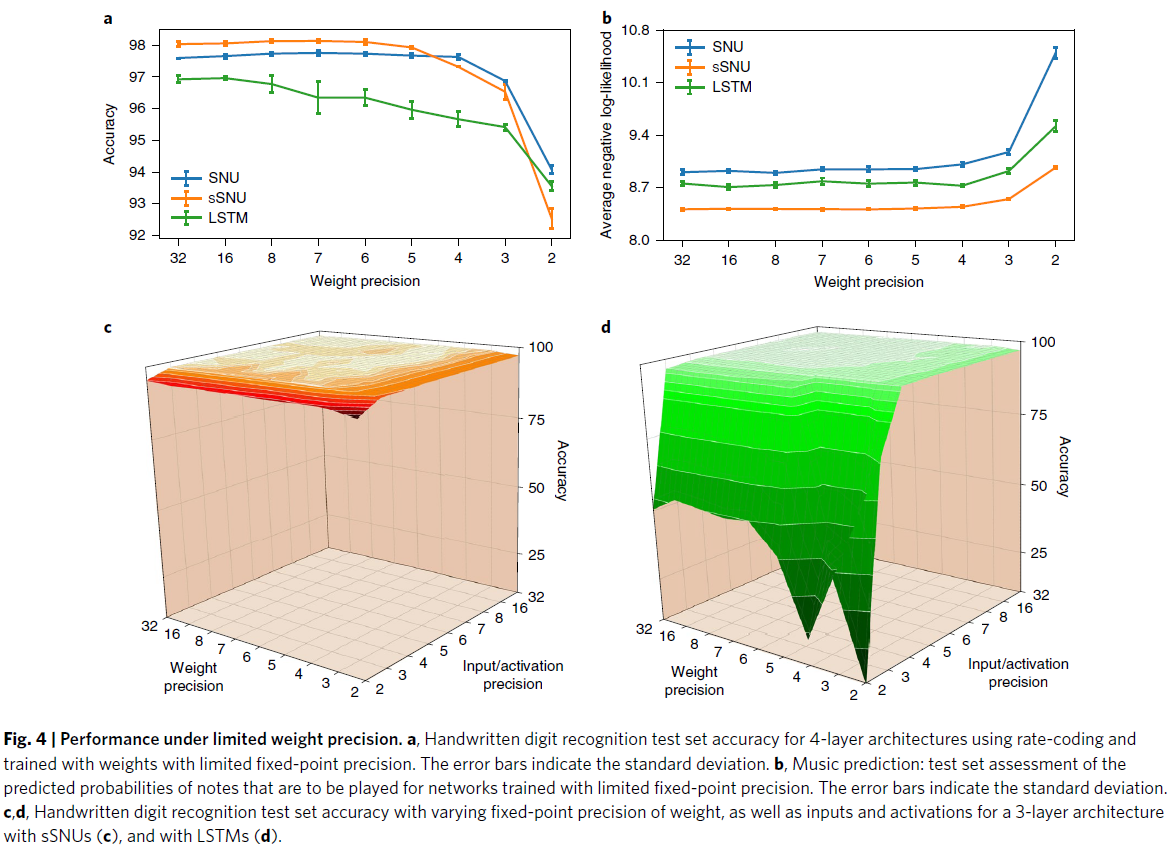
　　接下来，我们模拟了将权重精度从32位浮点数限制为定点表示的影响，精度值范围从32位到2位，模拟了神经形态硬件中有限精度的影响。我们比较了4层架构的性能，它在手写数字识别任务的全连接架构中表现最好。如图4a所示，虽然LSTM性能在16位以下开始恶化，但SNU性能保持稳定至6位。即使在4位时，基于SNU的网络也比基于LSTM的网络获得了更高的精度，并且具有32位定点精度。接下来，我们对音乐预测任务进行了类似的模拟。图4b说明所有单元在精度降低到4位时仍然保持稳健。因此，为了在神经形态硬件中训练基于SNU的网络，突触权重应至少提供4位精度。

　　最后，图4c,d说明了对手写数字识别任务的实值变体的权重和输入/激活值使用具有可变精度的定点算术时对性能的影响。扩展数据图5中报告了具有标准偏差的精度值。可以看出，sSNU比LSTM更好地处理低精度状态。具体来说，当输入/权重/激活的精度值低于4位时，基于LSTM的网络学习困难，最终达到更差的精度。另一方面，对于权重、输入和激活的精度值约为4位的基于sSNU的网络，观察到了边际性能下降。对于低于4位的精度值，性能仅略微下降至92.4%。

　　上述结果证明了SNU在低精度状态下的鲁棒性，使其在硬件加速器中的实现具有吸引力。特别是，基于新兴忆阻存储器技术(例如PCM)的内存计算加速器提供了高能效的非易失性多级存储，适用于高度集成的突触权重实现。

PCM-based in-memory acceleration

Conclusion

Methods

Data availability

Code availability