Finite Meta-Dynamic Neurons in Spiking Neural Networks for Spatio-temporal Learning

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布

arXiv:2010.03140v1 [cs.NE] 7 Oct 2020

Abstract

　　脉冲神经网络(SNN)包含了更多生物学合理的结构和学习原理，因此在弥合人工神经网络和自然神经网络之间的差距方面发挥着关键作用。脉冲是描述高于阈值的基于事件的发放和低于阈值的膜电位动态计算的稀疏信号，这为我们提供了一种替代的统一且有效的信息表征和计算方式。受生物网络的启发，其中无数元神经元集成在一起以实现各种认知功能，我们提出并构建了元动态神经元(MDN)，以改进SNN，从而在时空学习期间实现更好的网络泛化。MDN设计有基本的神经元动态，包含膜电位的一阶和二阶动态，包括一些超参数支持的空间和时间元类型。MDN首先从空间(MNIST)和时间(TIDigits)数据集生成，然后扩展到各种其他不同的时空任务(包括Fashion-MNIST、NETtalk、Cifar-10、TIMIT和N-MNIST)。与其他SOTA SNN算法相比，达到了相当的精度，并且使用MDN的SNN也比不使用MDN的SNN实现了更好的泛化。

Keywords: Spiking Neural Network, Biologically-plausible Computing, Meta Neurons, Neuronal Dynamics.

1. Introduction

2. Related works

3. Method

3.1. The architecture of SNN

3.2. The 2nd-order dynamic neurons in SNN

　　Izhikevich神经元[22]是具有标准二阶动态的神经元，如公式(1)所示，其中V_j(t)是膜电位，其单位为mV。(V_j(t))²的比例被精心设计为0.04，并且(V_j(t))¹(设置为5)和(V_j(t))⁰(设置为140)的比例也是如此。U_j(t)是钾离子电流激活和钠离子电流失活的膜恢复变量电荷，U_j(t)越大，V_j(t)越是超极化。发放后，动态V_j(t)和U_j(t)将分别重置为c和U_j(t) + d。公式(1)中的a、b、c和d是Izhikevich神经元的预定义超参数。

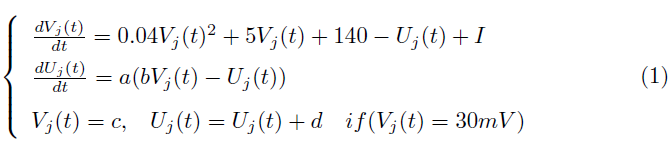
　　与Izhikevich神经元相似但不同的是，我们将二阶微分方程设计为基本神经元模型，没有任何预定义的(V_j(t))²、(V_j(t))¹和(V_j(t))⁰，如公式(2)所示，其中U_j(t)是模拟超极化的电阻项，θ_a、θ_b、θ_c和θ_d是区分膜电位V_j(t)的不同二阶动态的动态参数(我们选择不使用a、b、c和d以避免可能发生的混淆)。为简单起见，我们使用1而不是基本维度，例如mV，ms。

3.3. The procedure of generation and selection of the 2nd-order dynamic neurons

3.4. The traditional 1st-order dynamic neurons in SNN

3.5. Training SNN with approximate BP

　　传统的BP基于微分链式法则，其中L是标准损失函数，描述了平均输出重估和标签O_k的平方误差之和，其中k是神经元的id。

　　如公式(5)所示，对于标准BP，包含两部分：一是全局，另一部分是局部。然而，包含一个特殊的部分，它是一个无穷微分梯度，其中脉冲的微分是+∞或-∞，因此将截断链式法则并使标准BP无法训练SNN。

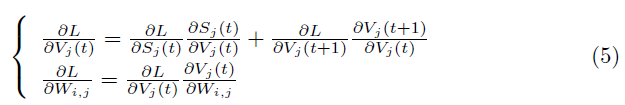
　　一个近似的BP技巧[24]可以很好地解决这个问题，通过定义一个伪微分梯度，在时间窗口内的脉冲时间为无限微分梯度定义下界和上限。

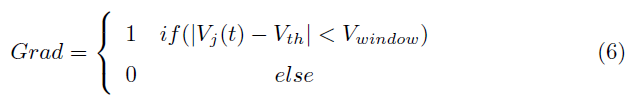
　　如公式(6)所示，V_j(t)是前馈传播阶段保存的膜电位，V_th是发放阈值，V_window是δt之间的膜电位范围，Grad是计算的梯度SNN中突触修饰的更新。该Grad不是+∞或-∞，因此可能会相应地传播梯度，而不会产生不微分冲突。

4. Experiments

4.1. The spatial and temporal datasets

4.2. The configurations and hyperparameter settings for following experiments.

4.3. The clustering of the 2nd-order MDNs

4.4. The filtering of 2nd-order meta neurons with memrbane-potential dynamics

4.5. Convergence analysis for the selected spatial and temporal meta neurons

4.6. Generalization analysis for the selected spatial and temporal meta neurons

4.7. The comparison of 1st- and 2nd-order neural dynamics

4.8. The analysis of spatio-temporal capability of dierent meta neurons

4.9. The comparison of our SNNs using MDNs with other SOTA SNN algorithms

5. Conclusion