定义
树
-
树(Tree)是 n(n~O) 个结点的有限集。n=O 时称为空树。
- 在任意一棵非空树中:有且仅有一个特定的称为根(Root)的结点
- 当n>1时,其余结点可分为m(m>O)个互不相变的有限集T1、T2、……、 Tm •其中每一个集合本身又是一颗树,并且称为根的子树(SubTree)
-
度
- 结点拥有的子树数称为树的度(Degree)
- 度为0的结点称为叶结点(终端结点)
- 度不为0的结点称为非终端结点(分支节点)
- 树中除了根节点,分支节点也被称为内部节点
- 树的度是树内各结点的度的最大值
-
树的深度
- 树中结点的最大层次称为树的深度(高度)
-
平衡因子(Balance Factor)
- 二叉树上结点的左子树的高度 减去 右子树的高度 的值 称为 平衡因子。因此平衡二叉树上所有结点的平衡因子只能是 0 ,1 ,-1。((AVL)平衡二叉树是一颗 二叉排序树 ,其中每个结点的左子树和右子树高度差至多等于1)
-
树的路径
- 路径长度:从一个节点到另一个节点之间的分支构成路径,路径上分支数目称做路径长度
- 带权路径长度(WPL):
当前节点p到根的路径长度与节点p的权值(权值为题中给的节点所占百分比)的乘积 - 树的路径长度:从根到各子节点的路径长度和
- 树的加权路径长度:从根到各子节点的加权路径长度和
- 扩展:赫夫曼树,带权路径长度(WPL)最小的
二叉树
特殊二叉树
-
斜树(左斜树/右斜树),即线性表
-
满二叉树
- 在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。
-
完全二叉树
- 对一棵具有 n 个结点的二叉树按层序编号,如果编号为 i (1<=i<=n) 的结点与同样深度的满二叉树中编号为i 的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树)
性质
- 第i层最多有多少个结点
- 深度为k的二叉树最多有多少结点
- 终端节点数(叶节点数)=度为2的节点数(n2)+1
- 具有n个结点的二叉树深度为(log2n)+1。(以2为底n的对数结果+1)
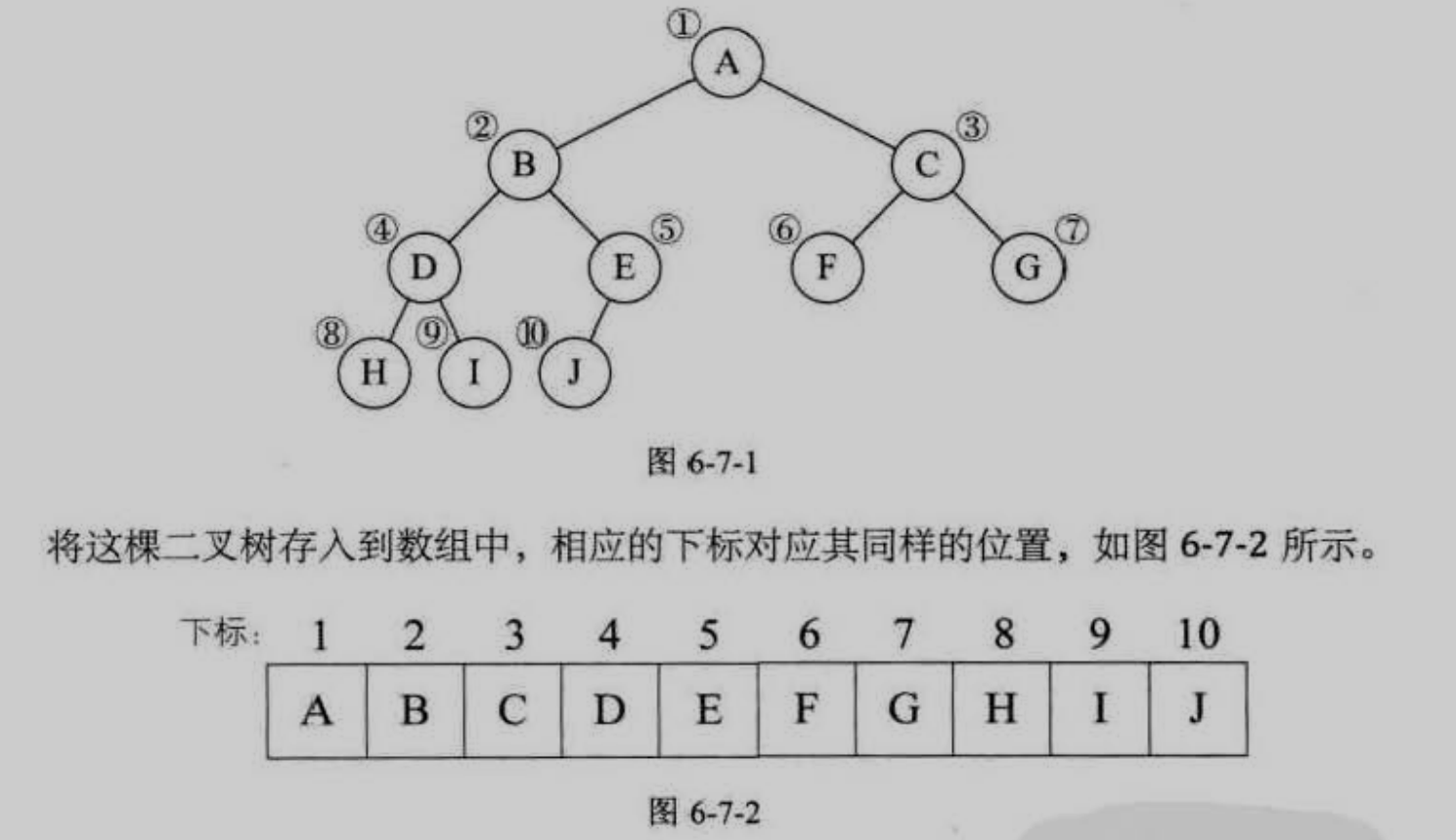
二叉树顺序存储结构
- 二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,井且结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系,适用于完全二叉树,斜树会造成空间浪费
便历二叉树
- 三种遍历都是从根结点开始
- (打印、左、右)前序遍历是先打印再递归左和右
- (左、打印、右)中序遍历是先递归左子树,打印,再递归右子树
- (左、右、打印)先递归左子树,再递归右子树,打印
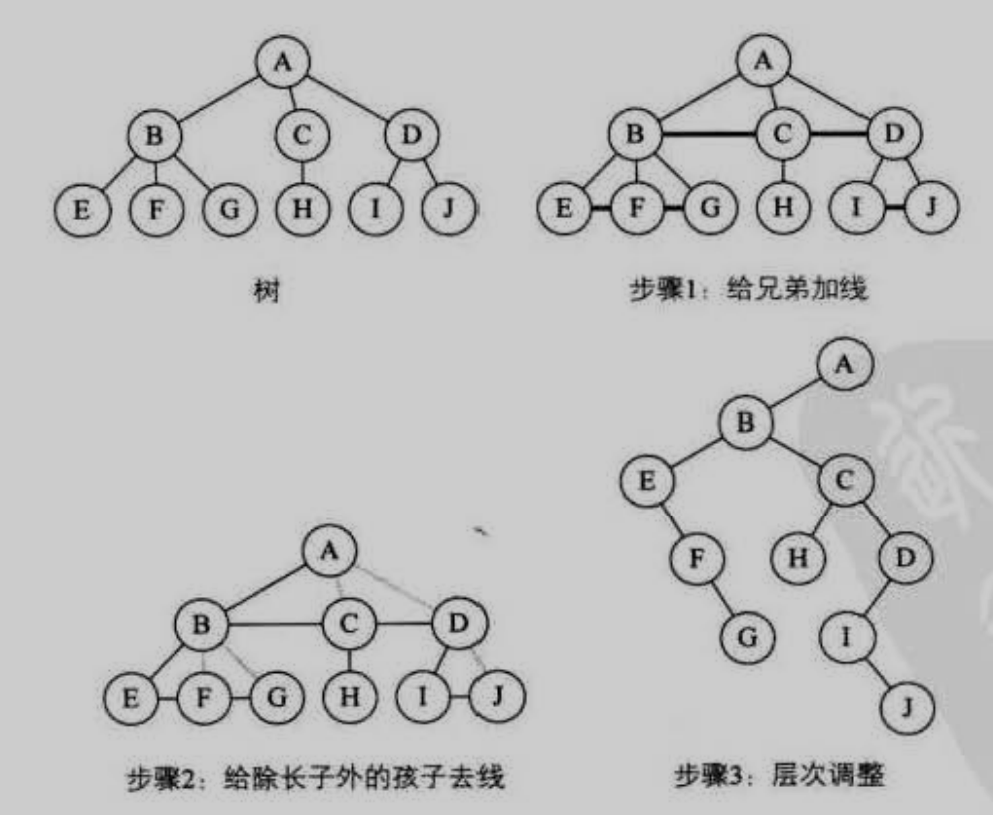
树转换为二叉树
- 连线。同层次兄弟连线
- 去线。从根结点开始,每个树只保留左子树
- 旋转调整。
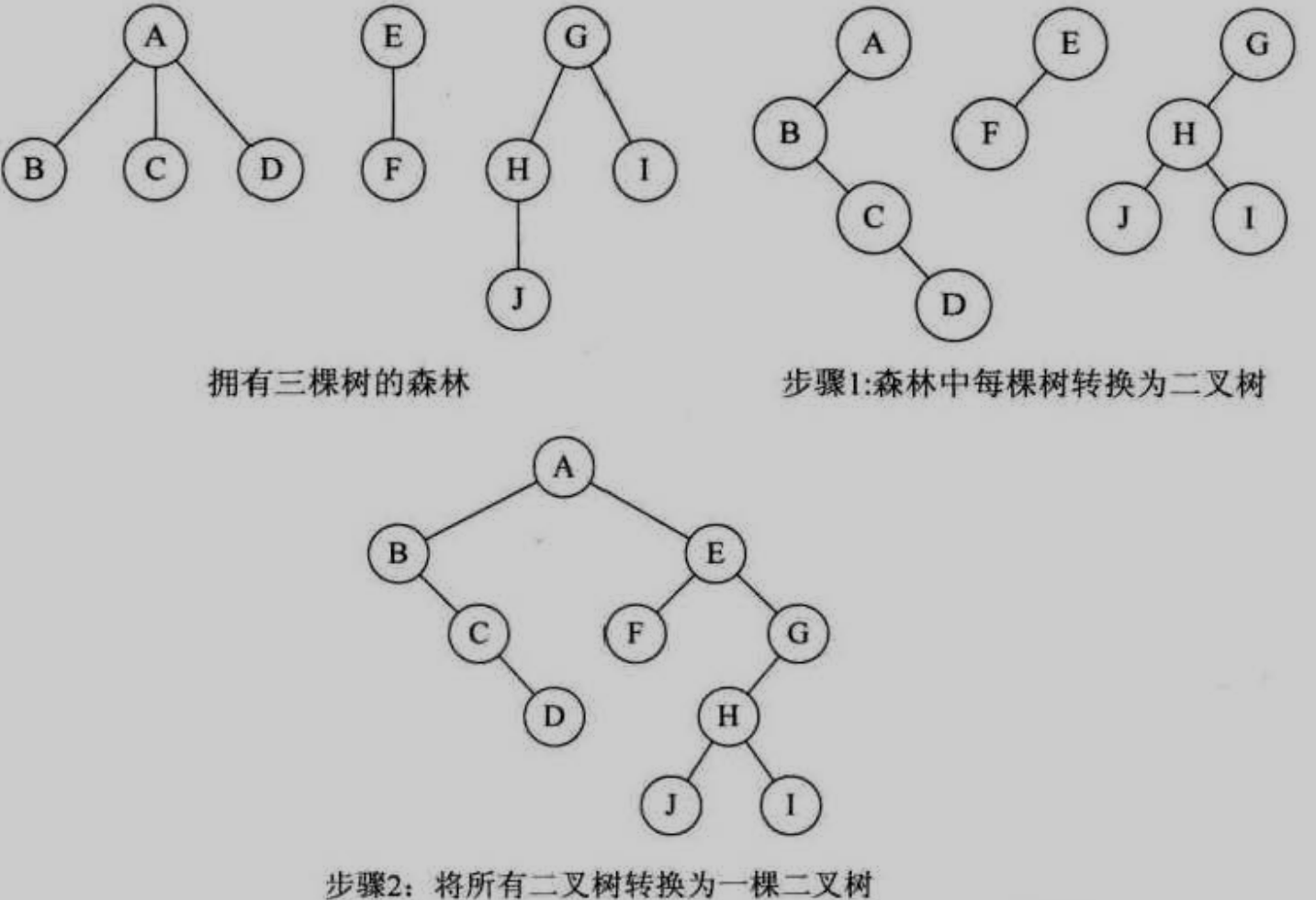
森林转化为二叉树
- 将每棵树分别转化为二叉树
- 从最后一棵树开始,将二叉树拼接到前一棵树的根点的右子树上
二叉树查找/插入/删除
- 查找:
- 插入:
- 删除:
- 叶子节点:直接删除
- 只有左(右)子树:直接删除结点,然后将它整个左(右)子树,整体移动到删除结点的位置即可
- 左右子树同时有:删除节点位于根节点左半的树,找到删除结点p的直接前驱(比p大的前驱),进行替换,然后删除;删除节点位于根节点右半的树,找到删除结点p的直接后继(比p大的后继),进行替换,然后删除
常见树的特点
二叉排序树(BST,二叉搜索树,二叉查找树),树非空的情况下
- 若左子树不空,则
左子树上的所有结点值均小于它的根结点的值 - 若右子树不空,则
右子树上的所有结点值均大于它的根结点的值 - 它的左子树与右子树分别也是一棵
二叉排序树
平衡二叉树是一棵每个结点的左子树 与 右子树 高度差 <=1的二叉排序树
- 原理:在构建
二叉排序树的过程中,每当插入一个结点时,先检查是否因插入破坏了平衡性,若破坏了,则找出最下不平衡子树,在保持二叉排序树的特性下,调整最小不平衡子树中各结点间的链接关系,进行相应的旋转使之成为新的平衡子树。结点h插入值后