2-3查找树的定义(平衡树)
- 2-结点
- 含有
一个键(及其对应的值)和两条链,左链接指向2-3树中的键都小于该节点,右链接指向的2-3树中的节点都大于该结点
- 含有
- 3-结点
- 含有
两个键(及其对应的值)和三条链,左链接指向的2-3树中的键都小于该结点,中链接指向的2-3树中的键都位于该结点的两个键之间,右链接指向的2-3树中的键都大于该结点
- 含有
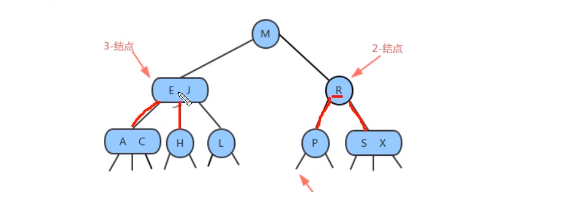
插入操作
-
向2- 结点中插入新键
- 找到键,将结点替换为一个新的含有k的3- 结点
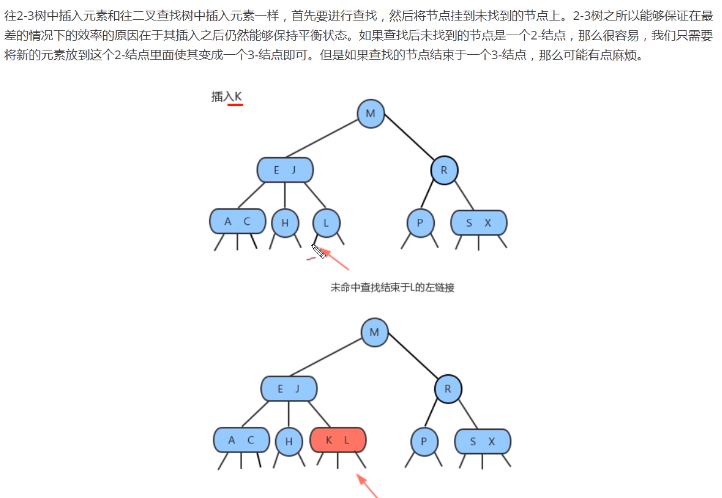
- 找到键,将结点替换为一个新的含有k的3- 结点
-
向3- 结点中插入新键
- 假如2-3树只包含一个3-结点,这个结点有两个键,没有空间来插入第三个键了,最自然的方式是我们假设这个点能存放三个元素,暂时使其变成一个4-结点,同时包含4条链接,然后我们将这个4-结点的中间元素提升,左边的键作为其左子结点,右边的键作为其右子结点。插入完成,变为
平衡2-3查找树,树的高度从0变为1
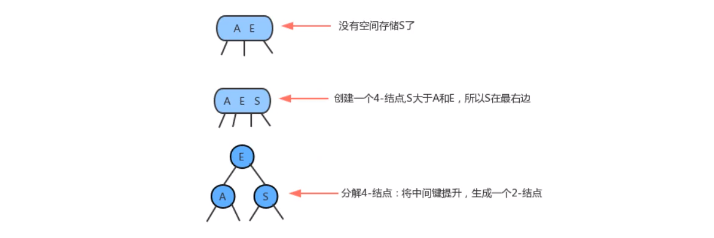
- 假如2-3树只包含一个3-结点,这个结点有两个键,没有空间来插入第三个键了,最自然的方式是我们假设这个点能存放三个元素,暂时使其变成一个4-结点,同时包含4条链接,然后我们将这个4-结点的中间元素提升,左边的键作为其左子结点,右边的键作为其右子结点。插入完成,变为
-
向一个父结点为2-结点的3-结点中插入新键
- 和上面的情况一样一样,我们也可以将新元素插入到3-结点中,使其成为一个临时的4-结点,然后,将该结点中的中间元素提升到父结点即2-结点中,使其父结点成为一个3-结点,然后将左右结点分表挂在这个3-结点的恰当位置
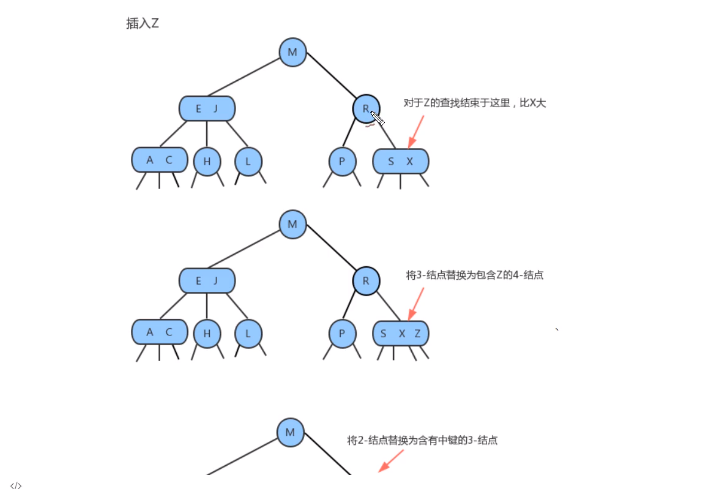
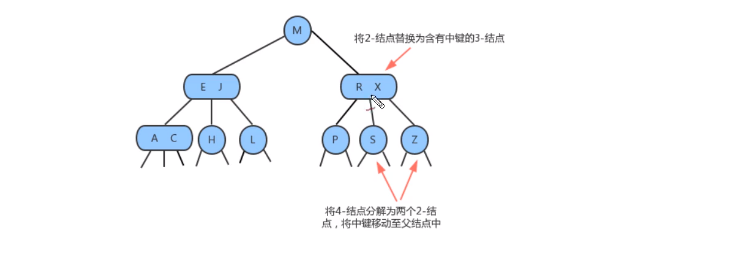
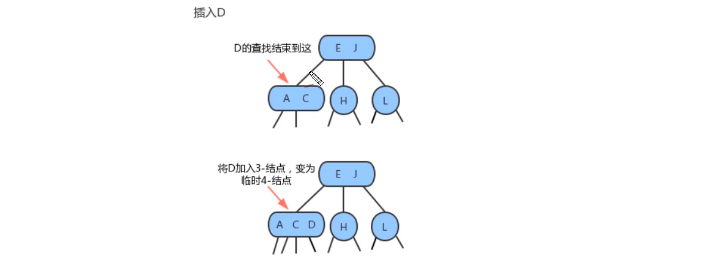
- 向一个父结点为3-结点的3-结点中插入新键
- 当我们插入的结点是3- 结点的时候,我们将该结点拆分,中间元素提升至父结点,但是此时父结点是一个3- 结点,插入之后,父结点变成了4- 结点,然后继续将中间元素提升至父结点,直至遇到一个父结点是2- 结点,然后将其变为3- 结点,不需要再次拆分
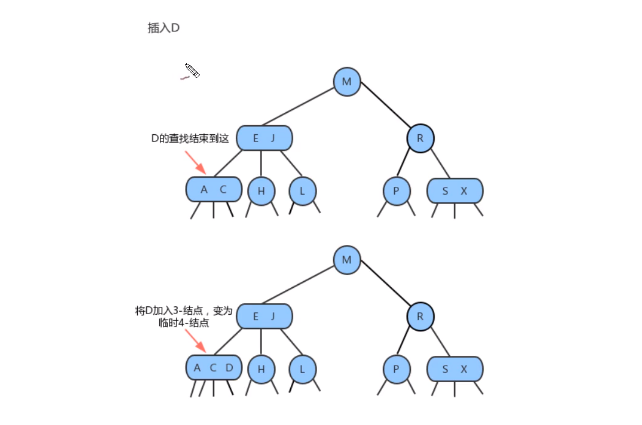
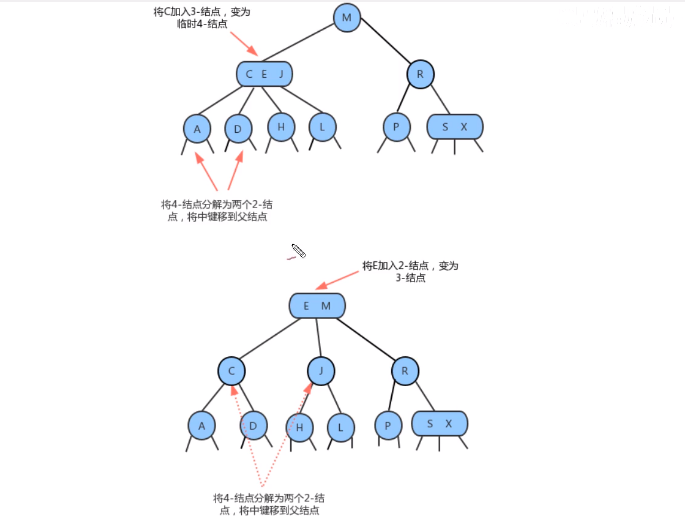
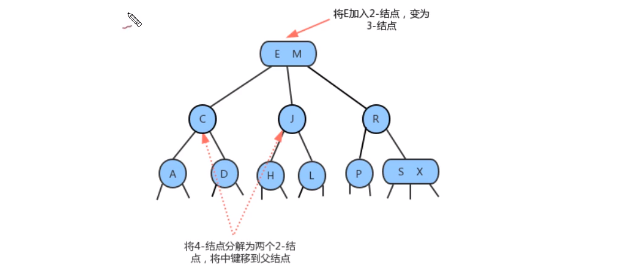
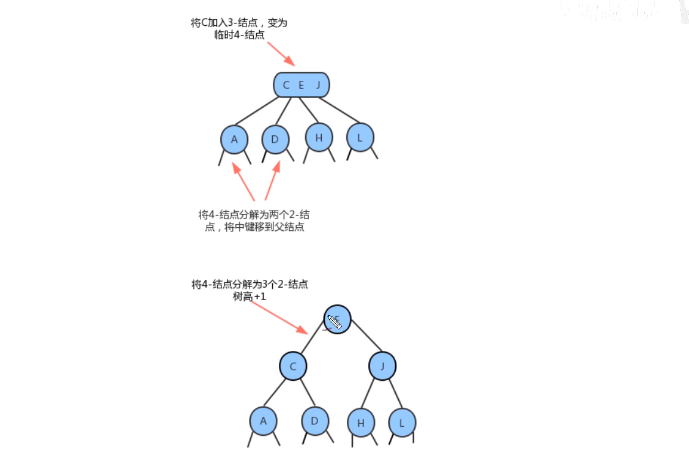
- 分解根结点
- 当插入的结点到根结点的路径上全部是3- 结点的时候,最终我们的根结点会变成一个
临时的4- 结点,此时,就需要将根结点拆分为两个2-结点,树的高度+1
- 当插入的结点到根结点的路径上全部是3- 结点的时候,最终我们的根结点会变成一个
2-3树的性质
-
对于一棵完全平衡的
2-3树- 任意的终端结点(无子树的叶结点)到根结点的路径长度都是相等的
4- 结点变换为3结点时,树的高度不会发生变化,只有当根结点是临时的4- 结点时,分解根结点时,树高度+1- 2-3 树与普通二叉查找树的最大区别在于,
普通的二叉查找树是自顶向下生长,而2-3 树是自底向上生长,因为2-3二叉树根结点子链只能是2或3,插入元素时,超过个数会将当前的多于的元素上移(向上生长)
-
笔记整理,学自Bilibili黑马