1.梯度下降


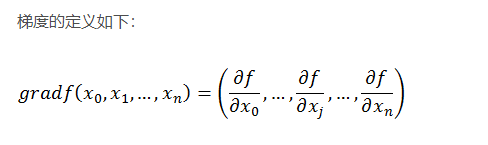
梯度的提出只为回答一个问题:函数在变量空间的某一点处,沿着哪一个方向有最大的变化率?
局部下降最快的方向就是梯度的负方向。
典例:下山问题。

假设我们位于黄山的某个山腰处,山势连绵不绝,不知道怎么下山。于是决定走一步算一步,也就是每次沿着当前位置最陡峭最易下山的方向前进一小步,然后继续沿下一个位置最陡方向前进一小步。这样一步一步走下去,一直走到觉得我们已经到了山脚。这里的下山最陡的方向就是梯度的负方向。
梯度下降算法公式:

推导过程:
一阶泰勒展开式:简单地来说,一阶泰勒展开式利用的就是函数的局部线性近似这个概念。我们以一阶泰勒展开式为例:

利用上述的一阶泰勒展开式继续推导:




2.方向传播


求解过程:
先正向,在反向。
(1)正向:
q=-2+5=3,f=q*z=3*(-4)=-12
(2)反向




