【数据结构】图的遍历

What is 遍历

访问图中的每一个元素一次，仅仅一次。访问，可以是输出打印，改写啊，这样的，根据ADT使用者的回调函数而定。

图的遍历常用的有2种：深度优先搜索，广度优先搜索。

深度优先搜索(Deepth First Search . DFS)

 深度优先搜索和树的先序遍历道理是一样的。

需要考虑以下几点：

1、为了避免重复访问，我们需要用一个  bool类型的访问标记数组（visited flag  array），来标记顶点是否已经被访问。

2、要考虑到 非连通图中的 “孤岛”，他们是孤立的子图，不能通过路径可达，但也要遍历到。

3、和树的遍历一样，有2种方法：递归和非递归。

说到这里，我又要吐槽书了，对！就是严蔚敏的数据结构。将visited访问标记数组定义为全局变量， 实在看不下去了。

我的改进是，用“壳子”函数 ArrayGraph_DFS来创建局部访问标记数组，而真正完成遍历的是ArrayGraph_DFS_traverse，

将visited作为ArrayGraph_DFS_traverse的参数传递，这样递归的各层

函数就能共享这个数组了。细心的同学发现我将ArrayGraph_DFS_traverse声明为static，其作用是隐藏ArrayGraph_DFS_traverse于此源文件。

可以将访问操作定义为一个回调函数，让API使用者决定如何访问。但是我没有这样做，而是硬编码，用printf打印作为访问操作。想写的简单些。

深度优先搜索的递归实现：

#include<stdio.h>
#define MAX_VERTEX  4

typedef char DataType;                 //图中元素的目标数据类型 


typedef struct    
{                  
    DataType vertexArr[MAX_VERTEX];        //顶点元素数组 

    int edgeArr[MAX_VERTEX][MAX_VERTEX];   //边矩阵二维数组 
    

}ArrayGraph;



void ArrayGraph_init(ArrayGraph *pGraph);
void ArrayGraph_create(ArrayGraph *pGraph);
void ArrayGraph_DFS(ArrayGraph * pGraph,int n);
static void  ArrayGraph_DFS_traverse(ArrayGraph * pGraph,int n,bool*visited);

int main()
{
    ArrayGraph g;
    ArrayGraph_init(&g);       //初始化图 
    ArrayGraph_create(&g);     //创建图 
    ArrayGraph_DFS(&g,3);       //遍历 ，从索引为3的顶点开始
return 0;
}



//初始化为一个无圈图 ，也就是边矩阵中，主对角线元素都是0 
void ArrayGraph_init(ArrayGraph *pGraph)
{
    
    for (int i = 0; i < MAX_VERTEX; i++)

        pGraph->edgeArr[i][i] = 0;

}


void ArrayGraph_create(ArrayGraph *pGraph)
{
    

    for (int i = 0; i < MAX_VERTEX; ++i)    //填充顶点数组，也就是输入顶点元素 
    {
        printf("输入第%d个顶点值
",i+1);
        
        scanf(" %c",&(pGraph->vertexArr[i])); 

    }

    for (int j = 0; j <MAX_VERTEX; ++j)   //填充边关系 
    {
        for (int i = j+1; i < MAX_VERTEX; ++i)
        {
            
            printf("若元素%c和%c有边，则输入1，否则输入0	",pGraph->vertexArr[j],pGraph->vertexArr[i]);
            
            scanf("%d",&( pGraph->edgeArr[j][i]));
            pGraph->edgeArr[i][j] = pGraph->edgeArr[j][i];     //对称 
        }
    }

}



static void  ArrayGraph_DFS_traverse(ArrayGraph * pGraph,int n,bool*visited)
{
    
    printf("%c	",pGraph->vertexArr[n]);

    visited[n] = true;

    for(int i=0;i<MAX_VERTEX;++i)    //以当前已访问的顶点为中心， 在其他所有的顶点中寻找
    {
        if(pGraph->edgeArr[n][i]!=0 && visited[i]==false)  //如果和当前顶点有边，且他们没有被访问过。则访问他们。
        {
            
            ArrayGraph_DFS_traverse(pGraph,i,visited);
        }
    }
    
    
    for(int i=0;i<MAX_VERTEX;++i)  //对图中可能出现的“孤岛”做一次清查 
      if(visited[i]==false)    //如果有孤岛存在，则用同样的方法，遍历他们。 
      {
           ArrayGraph_DFS_traverse(pGraph,i,visited);
      }

} 

void ArrayGraph_DFS(ArrayGraph * pGraph,int n)
{

    bool visited[MAX_VERTEX];      //访问标记数组，
    for(int i=0;i<MAX_VERTEX;++i)   //局部变量初始化
       visited[i] = false;         
      
      ArrayGraph_DFS_traverse(pGraph,n,visited);

}

看见递归，全局变量，老司机都会邹起眉头。原因不多说啊。下面是非递归实现。

非递归实现强调一个回退动作，当遍历到尽头时，需要退回来，尝试另一条支路，所以，在递进到下一层之前，我们需要保存此刻的顶点的索引到栈中，为回退做准备。

这个和狗狗在路边尿尿做标记很类似  ：）

对于非递归实现，附上一张gif图，便于理解非递归的方法  前进和回退 过程。这里画成了树结构，因为我觉得画成图了，看起来就很费劲了。树也是一种图，所以不影响的，道理是一样的。

50帧啊，一帧一帧的画，oh  my  god    (；′⌒` )    播放速度可能有点快，可以下载了用看图王 看。

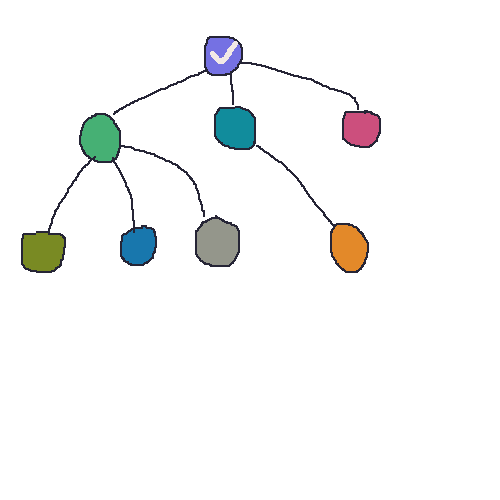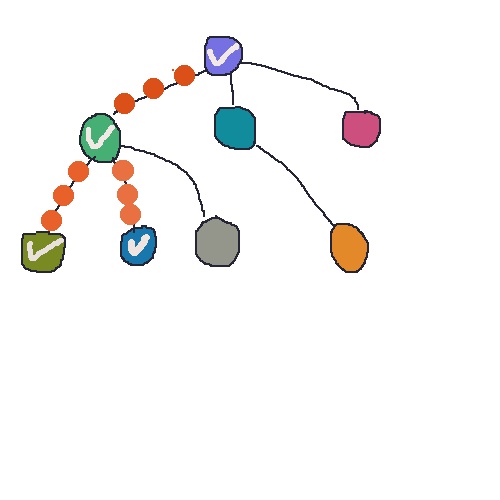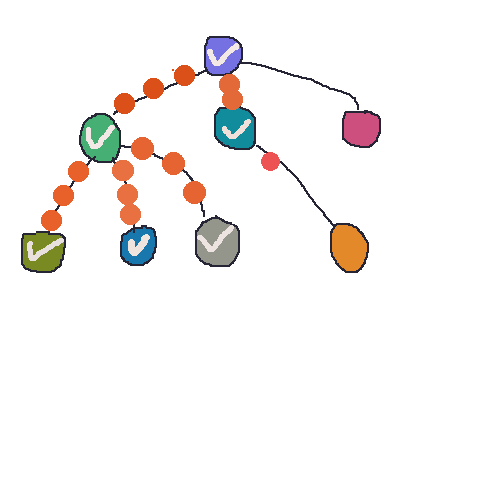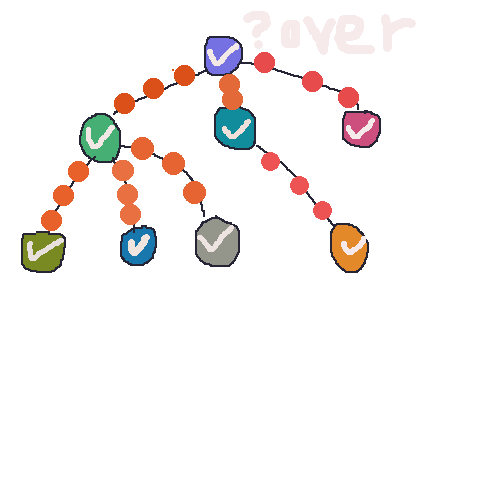
深度优先搜索的非递归实现：

#include<stdio.h>
#include<stack>

using std::stack;
#define MAX_VERTEX  4

typedef char DataType;                 //图中元素的目标数据类型 


typedef struct    
{                  
    DataType vertexArr[MAX_VERTEX];        //顶点元素数组 

    int edgeArr[MAX_VERTEX][MAX_VERTEX];   //边矩阵二维数组 
    

}ArrayGraph;


void ArrayGraph_init(ArrayGraph *pGraph);
void ArrayGraph_create(ArrayGraph *pGraph);
void ArrayGraph_DFS(ArrayGraph * pGraph,int n);


int main()
{
    ArrayGraph g;
    ArrayGraph_init(&g);       //初始化图 
    ArrayGraph_create(&g);     //创建图 
    ArrayGraph_DFS(&g,3);       //遍历 



    return 0;
}



//初始化为一个无圈图 ，也就是边矩阵中，主对角线元素都是0 
void ArrayGraph_init(ArrayGraph *pGraph)
{
    
    for (int i = 0; i < MAX_VERTEX; i++)

        pGraph->edgeArr[i][i] = 0;

}


void ArrayGraph_create(ArrayGraph *pGraph)
{
    

    for (int i = 0; i < MAX_VERTEX; ++i)    //填充顶点数组，也就是输入顶点元素 
    {
        printf("输入第%d个顶点值
",i+1);
        
        scanf(" %c",&(pGraph->vertexArr[i])); 

    }

    for (int j = 0; j <MAX_VERTEX; ++j)   //填充边关系 
    {
        for (int i = j+1; i < MAX_VERTEX; ++i)
        {
            
            printf("若元素%c和%c有边，则输入1，否则输入0	",pGraph->vertexArr[j],pGraph->vertexArr[i]);
            
            scanf("%d",&( pGraph->edgeArr[j][i]));
            pGraph->edgeArr[i][j] = pGraph->edgeArr[j][i];     //对称 
        }
    }


}



void ArrayGraph_DFS(ArrayGraph * pGraph,int n)
{
    
    bool visited[MAX_VERTEX];       //局部访问标记数组 
    for(int i=0;i<MAX_VERTEX;++i)   //局部变量需要手动初始化哦！ 
       visited[i] = false;          //局部变量是一次性数据，调用完，就回收。 
    
    
    bool  complete  = false;       //是否真正遍历完成？，主要用来对付非连通图
    
    stack<int> backStack;          //回退记录栈 

    int peekVertexIndex ;         //回退栈的栈顶存储的顶点的索引 
    int i;

    do{
    

        printf("%c	",pGraph->vertexArr[n]);    //访问当前子图的源点，first blood！！！
        visited[n] = true;
        backStack.push(n);
    
        while(!backStack.empty())     //当回退栈为空时，说明已经无路可退，顶点遍历完了 
        {
            peekVertexIndex = backStack.top();  //从先前访问过的顶点开始
    
            for(i=0;i<MAX_VERTEX;++i)
            {
                                              //寻找他的一个未被访问的邻接点
                if(pGraph->edgeArr[peekVertexIndex][i]!=0 && visited[i]== false)   
                {
                    printf("%c	",pGraph->vertexArr[i]);   //一旦找到一条可行的支路连接的新顶点，则访问它 
    
                    visited[i] = true;
                    backStack.push(i);                     //访问过后，将他入栈，作为新的栈顶元素。 
                    break;              
    
                }
                
            }
    
            if(i==MAX_VERTEX)       //一个前进的路径也没找到，说明到了某条支路的尽头，或者此顶点的邻结点都被访问过了 
            {
                backStack.pop();    //回退，尝试先前访问过的顶点的另一条支路 
            }
    
        
    
         } //end of while
         
         complete = true;    //当遍历完一个连通子图后，假定完成了所有的遍历 
         
         for(i = 0;i<MAX_VERTEX;++i) //对所有的顶点清查， 
         {
             if(visited[i]==false)    //发现还有顶点没访问到，出现了孤岛 
             {
                 complete = false;    //将完成标记 置为false 
                 n = i;               //记下这个孤岛的源顶点点索引 
                 break;
            }  
             
         }
     
    }while(!complete);        //没有真正完成所有的遍历，则再来一次 
}

 记得看过一本书上说：过多的注释是对自己代码的不自信，我觉得这话有道理。但是注释就是代码的笔记，多一点总比少一点好吧。

广度优先搜索(Breadth First Search . BFS)

广度优先搜索和数的层遍历也是一个道理。

它对有向图和无向图都适用。

它同样需要访问标记数据，同样需要考虑非连通图的问题。

同样我也用了gif图来宏观的描述这个过程。（我怀疑我是个图形极客  - - ！ ）

可以发现，当发现一个可以访问的顶点后，广度优先搜索不会像深度优先搜索那么立刻递进到下一层，而是再去找同层的“兄弟”顶点，直到同层再也找不到更多的可访问的“兄弟”了，才进入下一层。这个差异在代码中就是 break的有无体现出来的。

从这点差异我们也可以体会到，为什么一个叫深度优先，一个叫广度优先。深度优先搜索是先纵向伸展开，而广度优先则是先横向拉伸。

 同一层的顶点是用队列来存储的。我用了C++ STL中的queue模版类。

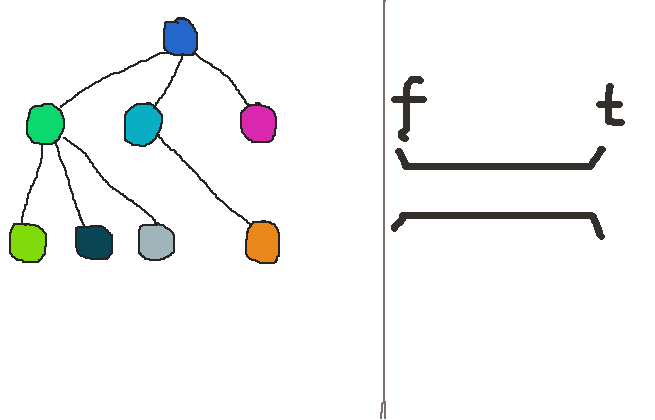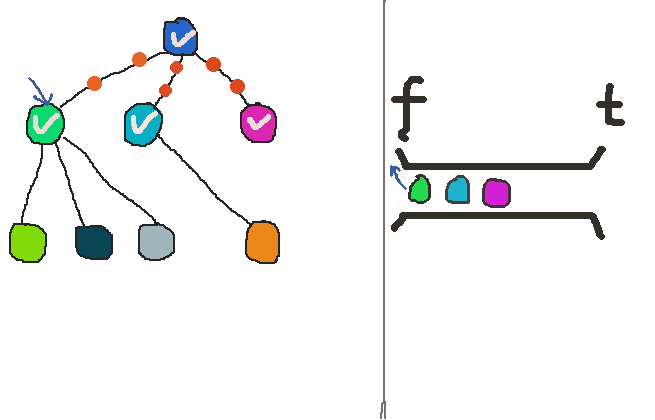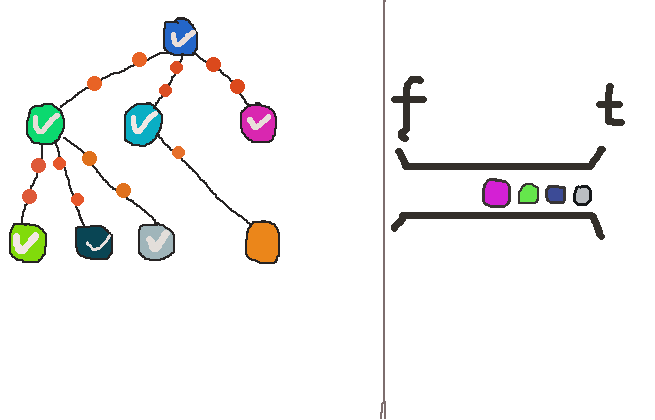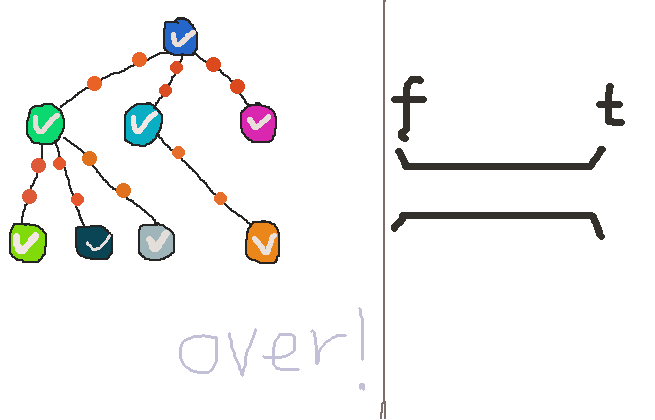
代码：

#include<stdio.h>
#include<queue>

using std::queue;
#define MAX_VERTEX  4

typedef char DataType;                 //图中元素的目标数据类型 


typedef struct    
{                  
    DataType vertexArr[MAX_VERTEX];        //顶点元素数组 

    int edgeArr[MAX_VERTEX][MAX_VERTEX];   //边矩阵二维数组 
    

}ArrayGraph;


void ArrayGraph_init(ArrayGraph *pGraph);
void ArrayGraph_create(ArrayGraph *pGraph);
void ArrayGraph_BFS(ArrayGraph * pGraph,int n);


int main()
{
    ArrayGraph g;
    ArrayGraph_init(&g);       //初始化图 
    ArrayGraph_create(&g);     //创建图 
    ArrayGraph_BFS(&g,0);       //遍历 



    return 0;
}



//初始化为一个无圈图 ，也就是边矩阵中，主对角线元素都是0 
void ArrayGraph_init(ArrayGraph *pGraph)
{
    
    for (int i = 0; i < MAX_VERTEX; i++)

        pGraph->edgeArr[i][i] = 0;

}


void ArrayGraph_create(ArrayGraph *pGraph)
{
    

    for (int i = 0; i < MAX_VERTEX; ++i)    //填充顶点数组，也就是输入顶点元素 
    {
        printf("输入第%d个顶点值
",i+1);
        
        scanf(" %c",&(pGraph->vertexArr[i])); 

    }

    for (int j = 0; j <MAX_VERTEX; ++j)   //填充边关系 
    {
        for (int i = j+1; i < MAX_VERTEX; ++i)
        {
            
            printf("若元素%c和%c有边，则输入1，否则输入0	",pGraph->vertexArr[j],pGraph->vertexArr[i]);
            
            scanf("%d",&( pGraph->edgeArr[j][i]));
            pGraph->edgeArr[i][j] = pGraph->edgeArr[j][i];     //对称 
        }
    }


}



void ArrayGraph_BFS(ArrayGraph * pGraph,int n)
{
    
    bool visited[MAX_VERTEX];       
    for(int i=0;i<MAX_VERTEX;++i)   
       visited[i] = false;         
    
    
    bool  complete  = false;       
    
    queue<int> layerQueue;        //层队列   

    int frontVertexIndex ;         
    int i;

    do{
    

        printf("%c	",pGraph->vertexArr[n]);    
        visited[n] = true;
        layerQueue.push(n);
    
        while(!layerQueue.empty())     
        {
            frontVertexIndex = layerQueue.front();  //获取队列 队首顶点 
            layerQueue.pop();
            
            for(i=0;i<MAX_VERTEX;++i)
            {
                                              //将 队首顶点 的邻结点全部访问，并全部入栈 
                if(pGraph->edgeArr[frontVertexIndex][i]!=0 && visited[i]== false)   
                {
                    printf("%c	",pGraph->vertexArr[i]);   
    
                    visited[i] = true;
                    layerQueue.push(i);               
                                                       
    
                }
                
            }
    
          
         } //end of while
         
         complete = true;    //当遍历完一个连通子图后，假定完成了所有的遍历 
         
         for(i = 0;i<MAX_VERTEX;++i) //对所有的顶点清查， 
         {
             if(visited[i]==false)    //发现还有顶点没访问到，出现了孤岛 
             {
                 complete = false;    //将完成标记 置为false 
                 n = i;               //记下这个孤岛的源顶点点索引 
                 break;
            }  
             
         }
     
    }while(!complete);        //没有真正完成所有的遍历，则再来一次 
}

下一篇：图的最小生成树